虽说 DFT 不需要像 DTFT 那样算无穷多项了,但要算的东西也是挺多的,我们来分析一下复杂度:
\[X[k]=\sum_{n=0}^{N-1}x[n]W_N^{kn},\;k=0,1,\cdots,N-1\\ W_N^{kn}=e^{-2\pi kn/N}\]要计算出 $N$ 个 $X[k]$,必须进行 $N^2$ 次复数乘法和 $N(N-1)$ 次复数加法,时间复杂度为 $O(N^2)$。
假如有一个 44.1 kHz 采样率的 1s 音频,那么乘法的运算量大约是 1.94G,而现在的计算机处理速度也就 3~5GHz,也就是说 1s 也就算个几次 DFT,要是换以前的 CPU,估计得算一个星期😓。
但我们可以利用 DFT 中 $W_N^{kn}$ 的一些特殊性质来简化计算。比如说:$W_N^{k+\frac{N}{2}}=-W_N^k$,这样的话就可以减少一半的运算量,但时间复杂度还是 $O(N^2)$。如果用上其他性质,就能在 $O(n\log n)$ 时间内求出来,就得到我们的 FFT 算法。
基-2 FFT
DIT-FFT 算法
按时间抽取 FFT 算法(DIT-FFT,Decimation In Time FFT),也叫 Cooley-Tukey Fast Fourier Transform,是 1965 年由 Cooley 和 Tukey 提出,现在使用的大部分 FFT 都是在这个算法的基础上进行改进的。这个算法的步骤如下:
设序列 $x[n]$ 的长度 $N$ 是 $2$ 的幂,我们将 $x[n]$ 分解为偶数点和奇数点:
\[\begin{aligned} x_1 [r] &= x[2r]\\ x_2 [r] &= x[2r+1] \end{aligned}\; r=0,1,\cdots,\frac{N}{2}-1\]从而 $X[k]$ 可以分解为:
\[\begin{aligned} X[k]&=\sum_{n = 偶} x[n] W_N^{kn}+\sum_{n = 奇} x[n] W_N^{kn}\\ &=\sum_{r=0}^{N/2-1} x[2r] W_N^{2kr}+W_N^{k} \sum_{r=0}^{N/2-1} x[2r+1] W_N^{2kr}\\ &=\sum_{r=0}^{N/2-1} x[2r] (W_N^{2})^{kr}+W_N^{k} \sum_{r=0}^{N/2-1} x[2r+1] (W_N^{2})^{kr} \end{aligned}\]由于 $W_N^2=W_{N/2}$,所以(注意 $k$ 的取值范围):
\[\begin{aligned} X[k]&=\sum_{r=0}^{N/2-1} x[2r] W_{N/2}^{kr}+W_N^{k} \sum_{r=0}^{N/2-1} x[2r+1] W_{N/2}^{kr}\\ &=X_1[k]+W_N^k X_2[k] \quad k=0,1,\cdots,N-1 \end{aligned}\]根据 $W_N^{k+\frac{N}{2}}=-W_N^k$,如果要算 $X[k+\frac{N}{2}]$,易得:
\[X[k+\frac{N}{2}] = X_1[k]-W_N^k X_2[k] \quad k=0,1,\cdots,N-1\]总的来说,这是一次蝶形运算,运算量是 1 乘 2 加。

利用这个思想,我们可以进行递归:
\[\log_2 N \begin{cases} \quad\quad\quad\quad N\\ \quad\quad\quad\swarrow \quad\searrow\\ \quad\quad N/2 \quad\; N/2\\ \quad\;\swarrow \quad\searrow \;\; \swarrow \quad\searrow\\ N/4 \;\; N/4 \; N/4 \;\; N/4\\ \quad\quad\quad\quad\;\vdots\\ \end{cases}\]每级的蝶形运算有 $N/2$ 个,每个蝶形运算包括一个复数乘法和两个加法,一共有 $\log_2 N$ 级,所以复杂度为 $O(N\log N)$
以 $N=8$ 为例:
| 计算流图 | 树形图 |
|---|---|
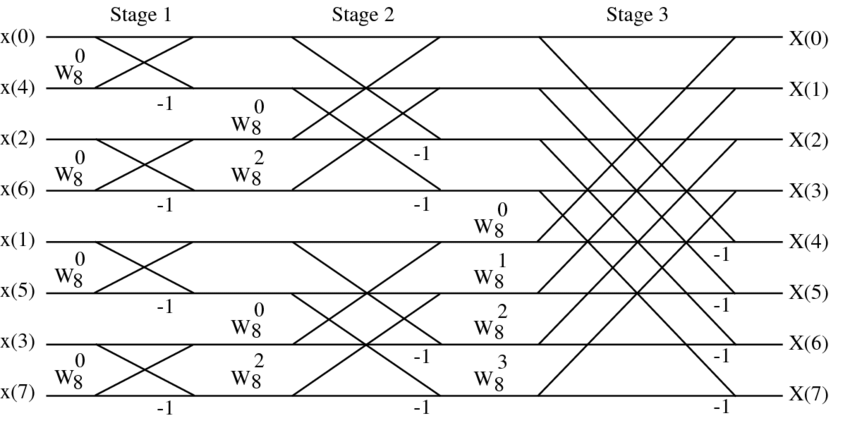 |
-01.png) |
我们来看看一个比较有趣的东西。将树形图中的编号写成二进制的形式:
| $X_0=00\red0$ | $X_1=00\red1$ | $X_2=01\red0$ | $X_3=01\red1$ | $X_4=10\red0$ | $X_5=10\red1$ | $X_6=11\red0$ | $X_7=11\red1$ |
| $00\red0$ $01\red0$ $10\red0$ $11\red0$ |
$00\red1$ $01\red1$ $10\red1$ $11\red1$ |
||||||
| $0\red00$ $1\red00$ |
$0\red10$ $1\red10$ |
$0\red01$ $1\red01$ |
$0\red11$ $1\red11$ |
||||
| $x_0=\red000$ | $x_4=\red100$ | $x_2=\red010$ | $x_6=\red110$ | $x_1=\red001$ | $x_5=\red101$ | $x_3=\red011$ | $x_7=\red111$ |
注意到,从上往下先是按二进制的第1位分奇偶,然后再按第2位、第三位……,最终,使得最下面与最上面的二进制恰好“对称”,这称为 比特逆序。
如果我们定义第 $r$ 级蝶形运算的输入是 $\Psi_r[\alpha]$ 和 $\Psi_r[\beta]$,并且特殊的,对于第一级,$\Psi_r[k]$ 对应的是比特逆序的 $k$,对于最后一级则是正常的 $k$。则每个蝶形运算可以表示为:
\[\Psi_{r+1}[\alpha] = \Psi_r[\alpha]+W_N^\ell \Psi_r[\beta]\\ \Psi_{r+1}[\beta] = \Psi_r[\alpha]-W_N^\ell \Psi_r[\beta]\]$\alpha$,$\beta$,$r$,$\ell$ 之间满足一些关系:
- $\alpha=a\cdot 2^r+b$,其中,$a=0,1,\cdots,N/2^r-1$,而 $b=0,1,\cdots,2^{r-1}-1$
- $\beta$ 与 $\alpha$ 一一对应,$\beta=\alpha+2^{r-1}$
- $\ell=b\cdot N/2^r$
我推导上面的式子只是为了好玩而已,课本中有库利-图基FFT算法的一般形式。考试中最好还是列计算流图。
DIF-FFT
按频率抽取(Decimation In Frequency)FFT 算法可以简单理解为 DIT-FFT 的翻转版。我们不将 $x[n]$ 进行奇偶分解,而是对 $X[k]$ 进行奇偶分解:
\[\begin{aligned} X[2r]&=\sum_{n=0}^{N-1} x[n] W_N^{n(2r)}\\ &=\sum_{n=0}^{N/2-1} x[n] W_N^{n(2r)}+\sum_{n=N/2}^{N-1} x[n] W_N^{n(2r)}\\ &=\sum_{n=0}^{N/2-1} x[n] W_N^{n(2r)}+W_N^{Nr}\sum_{n=0}^{N/2-1} x[n+N/2] W_N^{n(2r)}\\ &=\sum_{n=0}^{N/2-1} (x[n]+x[n+N/2]) W_{N/2}^{nr}\,,r=0,1,\cdots,N/2-1 \end{aligned}\] \[\begin{aligned} X[2r+1]&=\sum_{n=0}^{N-1} x[n] W_N^{n(2r+1)}\\ &=\sum_{n=0}^{N/2-1} x[n] W_N^{n(2r+1)}+\sum_{n=N/2}^{N-1} x[n] W_N^{n(2r+1)}\\ &=\sum_{n=0}^{N/2-1} x[n] W_N^{n(2r+1)}+W_N^{(Nr+N/2)}\sum_{n=0}^{N/2-1} x[n+N/2] W_N^{n(2r+1)}\\ &=\sum_{n=0}^{N/2-1} (x[n]-x[n+N/2]) W_N^r W_{N/2}^{nr}\,,r=0,1,\cdots,N/2-1 \end{aligned}\]DIF-FFT 与 DIT-FFT 蝶形运算的对比如下:

8 点 FFT 的计算流图如下:
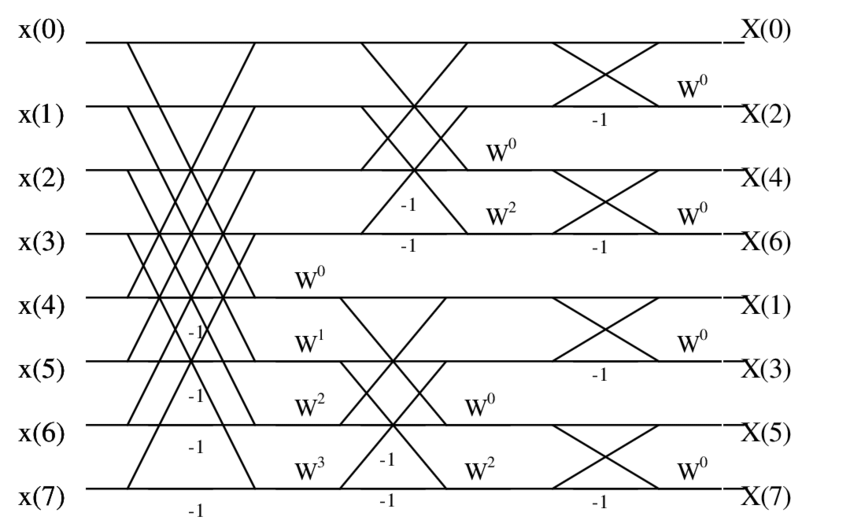
注意到 $x[n]$ 是比特顺序,$X[k]$ 是比特逆序,这恰好与 DIT-FFT 相反。
算法实现
FFTW 是一个用于计算 DFT 的 C 语言库,它是开源的~
参考
- 课本:数字信号处理——基于计算机的方法(第四版)
- 从多项式乘法到快速傅里叶变换