滤波器设计实验

$\begin{align*} \newcommand{\dif}{\mathop{}\!\mathrm{d}} \newcommand{\belowarrow}[1]{\mathop{#1}\limits_{\uparrow}} \newcommand{\bd}{\boldsymbol} \newcommand{\L}{\mathscr{L}} \newcommand{\xleftrightarrow}[1]{\stackrel{#1}{\longleftrightarrow}} \end{align*}$

姓名：周镇峰
学号：201830260422
班级：2018电子科学与技术卓越班

数字信号处理实验三

实验目的

利用窗函数法和等波纹滤波器法设计 FIR 滤波器
利用脉冲响应不变法和双线性变换法设计 IIR 滤波器
利用 STFT 进行参数分析

实验内容

利用 Matlab 编程，分别用窗函数法和等波纹滤波器法设计两种 FIR 数字带通滤波器，指标要求如下：
- 通带边缘频率 $\Omega_{P1}=0.45\pi$，$\Omega_{P2}=0.65\pi$，通带峰值起伏：$\alpha_P \leq 1$ dB
- 阻带边缘频率 $\Omega_{S1}=0.3\pi$，$\Omega_{S1}=0.75\pi$，最小阻带衰减 $\alpha_S \geq 40$ dB
利用 Matlab 编程，用脉冲响应不变法和双线性变换法设计一个数字带通滤波器，指标要求如下：
- 通带边缘频率 $\Omega_{P1}=0.45\pi$，$\Omega_{P2}=0.65\pi$，通带峰值起伏：$\alpha_P \leq 1$ dB
- 阻带边缘频率 $\Omega_{S1}=0.3\pi$，$\Omega_{S1}=0.8\pi$，最小阻带衰减 $\alpha_S \geq 40$ dB
线性调频信号LFM $x[nT]=\exp (j2\pi f_c nT + j \pi \mu (nT)^2)$，要求
1. 通过短时傅里叶变换，求给定起始频率 $f_c$ 和调频率 $\mu$ 的 LFM 信号的时频图
2. 查找其他参数估计方法，通过时频图重新估计 LFM 信号的起始频率和调频率

实验过程

设计 FIR 滤波器

窗函数法

窗函数法就是利用一个窗函数+时移，将无穷、非因果的理想滤波器转换为物理可实现的滤波器。加窗的过程如下图所示：

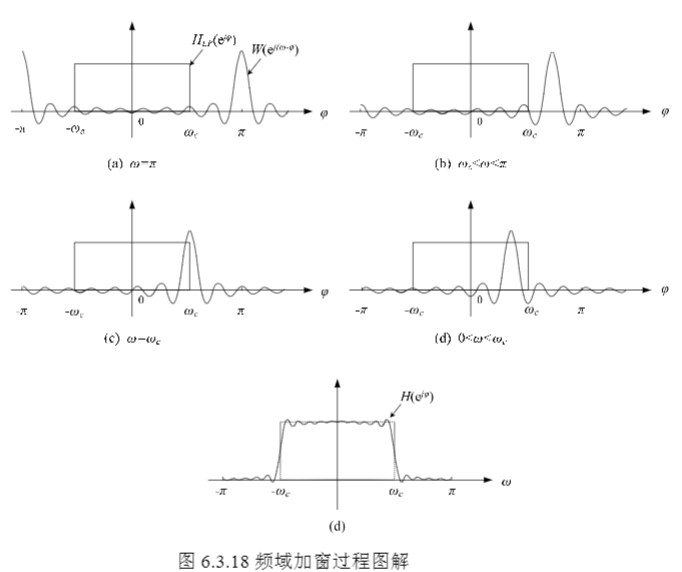
FIR 窗函数法

常见的窗函数的特性见下表：

窗类型	主瓣宽度	过渡带宽度	相对旁瓣水平	最小阻带衰减
矩形窗	4π/(2M+1)	0.92π/M	-13.3dB	-20.9dB
汉宁窗	8π/(2M+1)	3.11π/M	-31.5dB	-43.9dB
汉明窗	8π/(2M+1)	3.32π/M	-42.7dB	-54.5dB
布莱克曼窗	12π/(2M+1)	5.56π/M	-58.1dB	-75.3dB

根据题目要求，最小阻带衰减 $\alpha_S \geq 40$ dB，因此可以选择汉宁窗。

过渡带 $\Delta \Omega_1 = \Omega_{P1}-\Omega_{S1}=0.15\pi$，$\Delta \Omega_2 = \Omega_{S2}-\Omega_{P2}=0.1\pi$，取两者中较小的，代入上表中 $\Delta \Omega_2=3.11\pi/M$，可得 $M\approx 32$

利用 hamming(M) 函数生成 $M$ 长的汉明窗，并利用 fir1() 完成基于窗函数的 FIR 滤波器设计

wp=[0.45 0.65]; %通带
ws=[0.3 0.75]; %阻带
wc=(wp+ws)/2; %截止频率
as=40;
w=min(abs(wp-ws)); %过渡带
M=ceil(3.11/w); %长度
win=hamming(M+1);
boxb=fir1(M,wc,win);
freqz(boxb,1,512);

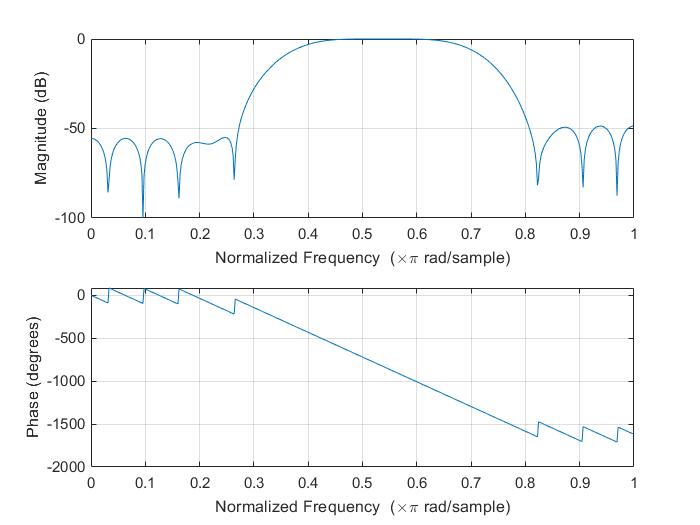
窗函数法设计FIR

等波纹滤波器法

等波纹最佳逼近法是一种优化设计法，即最大误差最小化准则，它克服了窗函数设计法和频率采样法的缺点，使最大误差（即波纹的峰值）最小化，并在整个逼近频段上均匀分布。用等波纹最佳逼近法设计的FIR数字滤波器的幅频响应在通带和阻带都是等波纹的，而且可以分别控制通带和阻带波纹幅度，这就是等波纹的含义。最佳逼近是指在滤波器长度给定的条件下，使加权误差波纹幅度最小化。与窗函数设计法和频率采样法比较，由于这种设计法使滤波器的最大逼近误差均匀分布，所以设计的滤波器性能价格比最高。阶数相同时，这种设计法使滤波器的最大逼近误差最小，即通带最大衰减最小，阻带最小衰减最大；指标相同时，这种设计法使滤波器阶数最低。

等波纹最佳逼近法的设计思想:用 $H_d(\omega)$ 表示希望逼近的幅度特性函数，要求设计线性相位FIR数字滤波器时,$H_d(\omega)$ 必须满足线性相位约束条件。用 $H(\omega)$ 表示实际设计的滤波器的幅度特性函数。定义加权误差函数$\varepsilon(\omega)$为：

\[\varepsilon(\omega)=W(\omega)[H_d(\omega)-H(\omega)]\]

式中，$W(\omega)$ 为幅度误差加权函数，用来控制不同频带（一般指通带和阻带）的幅度逼近精度。等波纹最佳逼近法的设计在于找到滤波器的系数向量 $h[n]$，使得在通带和阻带内的最大绝对值幅度误差 $

\varepsilon(\omega)

$为最小，这也就是最大误差最小化问题。

在 MATLAB 中，调用MATLAB信号处理工具箱函数remezord来计算等波纹滤波器阶数N和加权函数W(ω)，调用函数remez可进行等波纹滤波器的设计，直接求出滤波器系数。函数remezord中的数组fedge为通带和阻带边界频率，数组mval是两个边界处的幅值，而数组dev是通带和阻带的波动，fs是采样频率单位为Hz。

[n,fpts,mag,wt]=remezord([0.3 0.45 0.65 0.75],[0 1 0],[0.01 0.1087 0.01]);
%用remezord函数估算出remez函数要用到的阶n、归一化频带边缘矢量fpts、频带内幅值响应矢量mag及加权矢量w，
%使remez函数设计出的滤波器满足f、a及dev指定的性能要求。
h2=remez(n,fpts,mag,wt);%设计出等波纹滤波器
[hh2,w2]=freqz(h2,1,256);
figure(2)
subplot(2,1,1)
plot(w2/pi,20*log10(abs(hh2)))
grid
xlabel('归一化频率w');ylabel('幅度/db');
subplot(2,1,2)
plot(w2/pi,angle(hh2))
grid
xlabel('归一化频率w');ylabel('相位/rad');

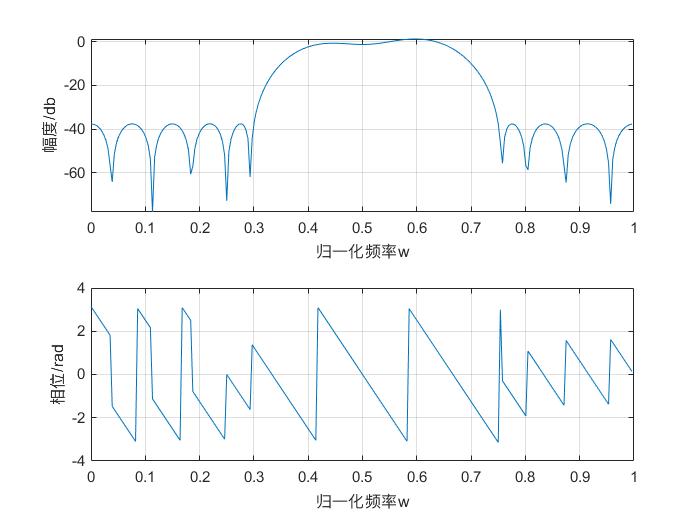
等波纹法设计FIR

设计 IIR 滤波器

总的来说，都是利用模拟滤波器来设计数字滤波器，根据转换的方法不同，分为：

冲激响应不变法
双线性变换法

冲激响应不变法

变换原理：数字滤波器的脉冲响应为 $h[n]$，模拟滤波器的冲激响应为 $h_a(t)$，冲激响应不变就是指这俩在 $t=nT$ 时相同，即：

\[h[n]=h_a(t) \Big\vert_{t=nT}\\ H(z)\Big\vert_{z=e^{sT}} = \hat{H}_a (s)=\frac{1}{T}\sum_{k=-\infty}^{+\infty} H_a \left( s-j\frac{2\pi}{T}k \right)\]

映射关系如下图（多对一）：

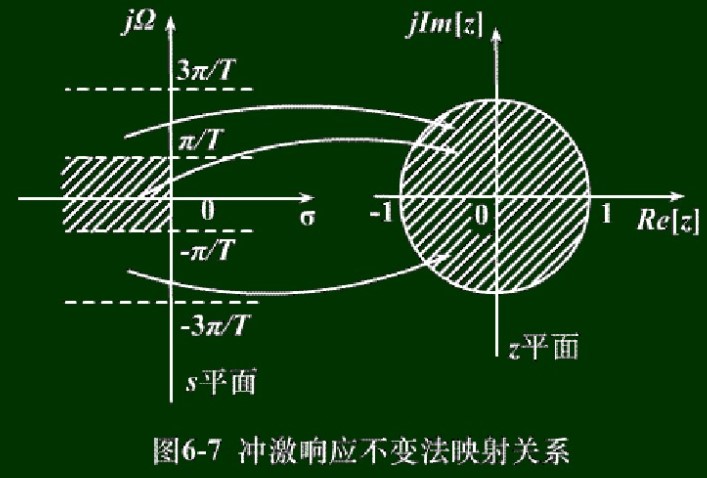
冲激响应不变法的映射关系

由于数字滤波器相当于对模拟滤波器在时域上采样，频域上进行周期延拓，所以只适合设计低通和带通滤波器（避免混叠）。这种方法的优点是时域逼近良好，且相位保持线性关系。

模拟到数字的转换过程如下：

\[H_a(s) \rightarrow h_a(t) \rightarrow h_a(nT) \rightarrow h(n) \rightarrow H(z)\]

$H_a(s)=\sum_{k=1}^N \dfrac{A_k}{s-p_k}$
$h_a(t)=\sum_{k=1}^N A_k e^{p_k t}u(t)$
$h(n)=h_a(nT)=\sum_{k=1}^N A_k (e^{p_kT})^n u(n)$
$H(z)=\sum_{n=-\infty}^\infty h(n)z^{-n}$ $=\sum_{n=0}^{\infty}\sum_{k=1}^N A_k \left( e^{p_kT}\right)^n z^{-n}$ $=\sum_{k=1}^N \frac{A_k}{1-e^{p_k T}z^{-1}}$

最终我们得到：

\[H_a(s)=\sum_{k=1}^N \frac{A_k}{s-p_k} \rightarrow H(z)=\sum_{k=1}^N \frac{A_k}{1-e^{s_kT}z^{-1}}\]

综上，设计过程是这样的：

选择 $T$，然后求出对应的模拟频率： $\Omega = \frac{\omega}{T}$
根据 $\Omega_p$，$\Omega_s$，$R_p$，$A_s$ 设计模拟滤波器
将 $H_a(s)$ 展开为部分分式的形式： $H_a(s)=\sum_{k=1}^{N} \frac{R_k}{s-p_k}$
将模拟转化为数字： $H(z)=\sum_{k=1}^N \frac{R_k}{1-e^{p_k T}z^{-1}}$

我们可以用 MATLAB 来辅助我们设计模拟滤波器。下面代码中的 buttord 和 butter 就是设计巴特沃斯滤波器。

T=1; %采样周期
fs=1/T; %采样频率
wp=[0.45*pi 0.65*pi]*fs; %通带
Ap=1; %通带峰值起伏dB
ws=[0.3*pi 0.8*pi]*fs; %阻带
As=40; %阻带峰值起伏dB
[N, wc]=buttord(wp,ws,Ap,As,'s'); %得到 buttonworth 滤波器的阶数N和截止频率wc
[B, A]=butter(N,wc,'bandpass','s'); %设计 buttonworth 滤波器，得到H(s)=B/A
w=linspace(0,pi,400*pi);
[D,C]=impinvar(B,A,fs); %模拟转数字
Hz=freqz(D,C,w);
plot(w/pi,abs(Hz));
grid on;
title('巴特沃斯带通滤波器');
xlabel('Frequency/Hz');
ylabel('Magnitude');

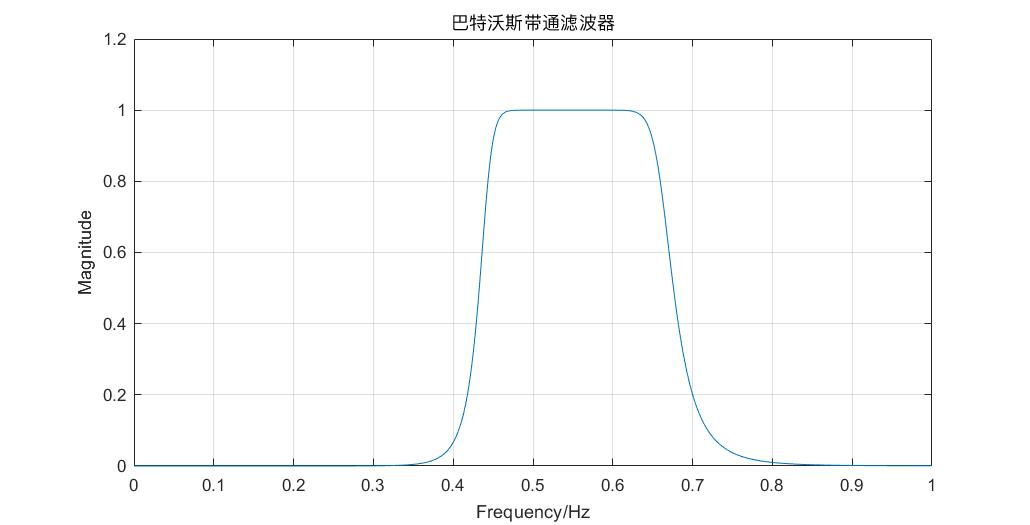
dsp巴特沃斯

我们也可以使用其他滤波器，比如切比雪夫I型滤波器：

T=1; %采样周期
fs=1/T; %采样频率
wp=[0.45*pi 0.65*pi]*fs; %通带
Ap=1; %通带峰值起伏dB
ws=[0.3*pi 0.8*pi]*fs; %阻带
As=40; %阻带峰值起伏dB
[N, wc]=cheb1ord(wp,ws,Ap,As,'s'); %得到 buttonworth 滤波器的阶数N和截止频率wc
[B, A]=cheby1(N,Ap, wc,'bandpass','s'); %设计 buttonworth 滤波器，得到H(s)=B/A
w=linspace(0,pi,400*pi);
[D,C]=impinvar(B,A,fs); %模拟转数字%冲激响应不变
Hz=freqz(D,C,w);
plot(w/pi,abs(Hz));
grid on;
title('切比雪夫Ⅰ型带通滤波器');
xlabel('Frequency/Hz');
ylabel('Magnitude');

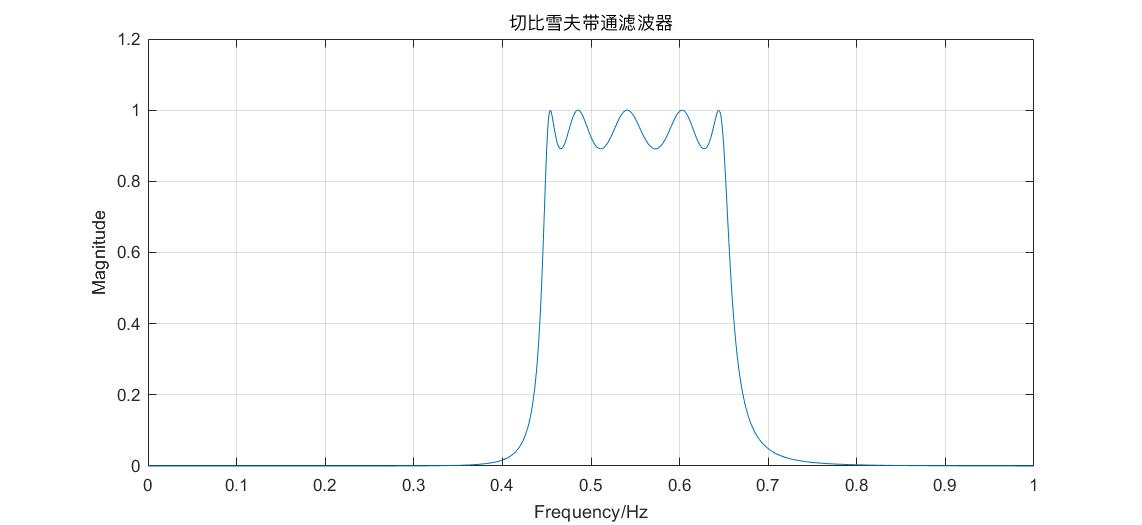
dsp切比雪夫1型

双线性变换法

双线性变换就是用了不同的 $s\rightarrow z$ 转换方法：

\[s=\frac{1-z^{-1}}{1+z^{-1}}\\ z=\frac{1+s}{1-s}\]

它的映射关系如下（一对一）：

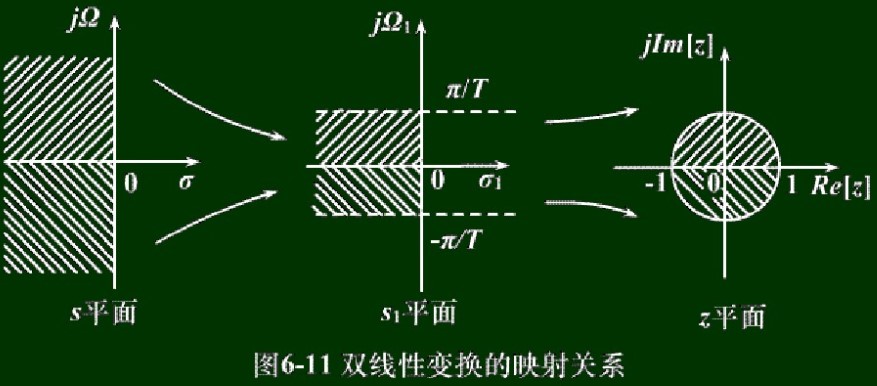
双线性变换法的映射关系

这种变换的优点就是：s平面与z平面是单值变换，所以避免了混叠。缺点就是：除了零频率附近，模拟频率 $\Omega$ 与数字频率 $\omega$ 之间非线性，因此要求幅度响应应该为分段常数型，否则会产生畸变。

公式的推导过程如下：

我们先将模拟频率 $\Omega=[-\infty,+\infty]$ 压缩到 $\Omega_1=[-\pi/T，\pi/T]$

\[\Omega=\tan \frac{\Omega_1 T}{2}\]

然后再将 $\Omega_1$ 映射到 $z$（就是冲激响应不变法中的过程）：

\[z=e^{s_1 T}\]

将两个结合起来，有：

\[\begin{aligned} \Omega&=\tan \frac{\Omega_1 T}{2}\\ &=\frac{\sin\frac{\Omega_1 T}{2}}{\cos\frac{\Omega_1 T}{2}}\\ &=\frac{e^{j\frac{\Omega_1 T}{2}}-e^{-j\frac{\Omega_1 T}{2}}}{2j}\bigg/ \frac{e^{j\frac{\Omega_1 T}{2}}+e^{-j\frac{\Omega_1 T}{2}}}{2} \end{aligned}\] \[\begin{aligned} s&=j\Omega\\ &=\frac{e^{j\frac{\Omega_1 T}{2}}-e^{-j\frac{\Omega_1 T}{2}}}{e^{j\frac{\Omega_1 T}{2}}+e^{-j\frac{\Omega_1 T}{2}}}\\ &=\frac{1-e^{-s_1 T}}{1+e^{-s_1T}}\\ &=\frac{1-z^{-1}}{1+z^{-1}} \end{aligned}\]

推导完毕。从上面推导中，可以注意到模拟频率 $\Omega$ 与数字频率 $\omega=\Omega_1 T$ 的对应关系不是线性的，而我们希望它越接近线性越好，于是我们进行一个拉伸操作：

\[\Omega = c \cdot \tan \frac{\omega}{2}\\ s = c \frac{1-z^{-1}}{1+z^{-1}}\\ z=\frac{c+s}{c-s}\]

若要求在低频处有比较明确的（线性）对应关系，那么：

\[\Omega_1 \approx \Omega = c \cdot \tan \frac{\Omega_1 T}{2} \approx c \cdot \frac{\Omega_1T}{2}\\ \Rightarrow c = \frac{2}{T}\]

从而双线性变换可以进一步写为：

\[s = \frac{2}{T} \left(\frac{1-z^{-1}}{1+z^{-1}}\right)\]

这正是课本中介绍的双线性变换，也是下面程序中用到的双线性变换。

若要求在某个频率 $\Omega_c\leftrightarrow \omega_c$ 处有比较明确的（线性）对应关系，那么：

\[\Omega_c = c \cdot \tan \frac{\omega_c}{2}\\ \Rightarrow c = \Omega_c \cot \frac{\omega_c}{2}\]

式中的 $\Omega_c, \omega_c$ 是自己设定的。

MATLAB 实现的代码如下：

T=1; %采样周期
fs=1/T; %采样频率
wp=[0.45*pi 0.65*pi]; %通带
Ap=1; %通带峰值起伏dB
ws=[0.3*pi 0.8*pi]; %阻带
As=40; %阻带峰值起伏dB

wp=(2/T)*tan(wp/2); %预扭曲%数字频率转模拟频率
ws=(2/T)*tan(ws/2);

[N, wc]=buttord(wp,ws,Ap,As,'s'); %得到 buttonworth 滤波器的阶数N和截止频率wc
[B, A]=butter(N,wc,'bandpass','s'); %设计 buttonworth 滤波器，得到H(s)=B/A
w=linspace(0,pi,400*pi);
[D,C]=bilinear(B,A,fs); %模拟转数字%双线性
Hz=freqz(D,C,w);
plot(w/pi,abs(Hz));
grid on;
title('巴特沃斯带通滤波器');
xlabel('Frequency/Hz');
ylabel('Magnitude');

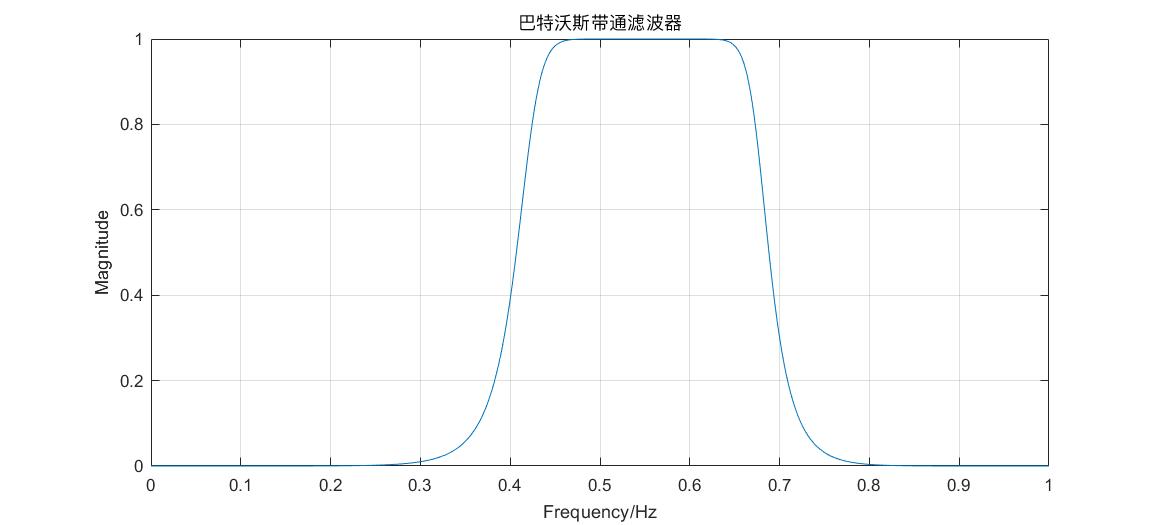
dsp巴特沃斯_双线性.jpg

利用 STFT 对 LFM 信号进行参数估计

可以利用 chirp() 函数生成 LFM 信号：

fs=1e3; %采样率
T=2; %脉冲宽度
N=fs*T; %采样点数
t=linspace(0, T, N);
f0=100; %起始频率
f1=400; %终止频率
y=chirp(t, f0, T, f1);
plot(t,y);

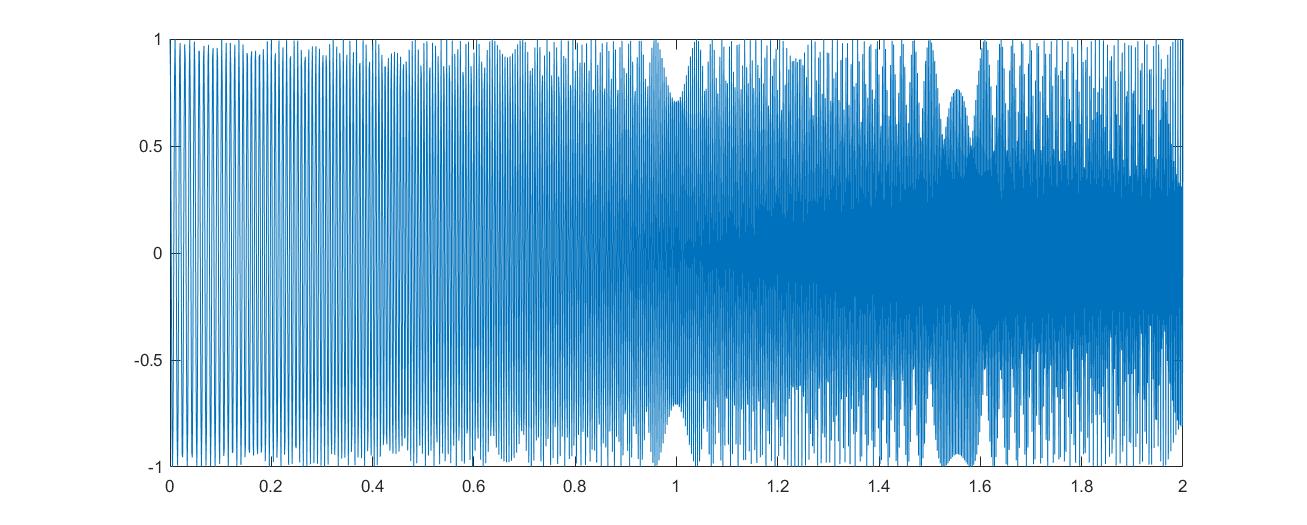
chirp信号

利用 spectrogram() 计算短时傅里叶变换：

spectrogram(y,128,100,128,1e3,'yaxis');

stft

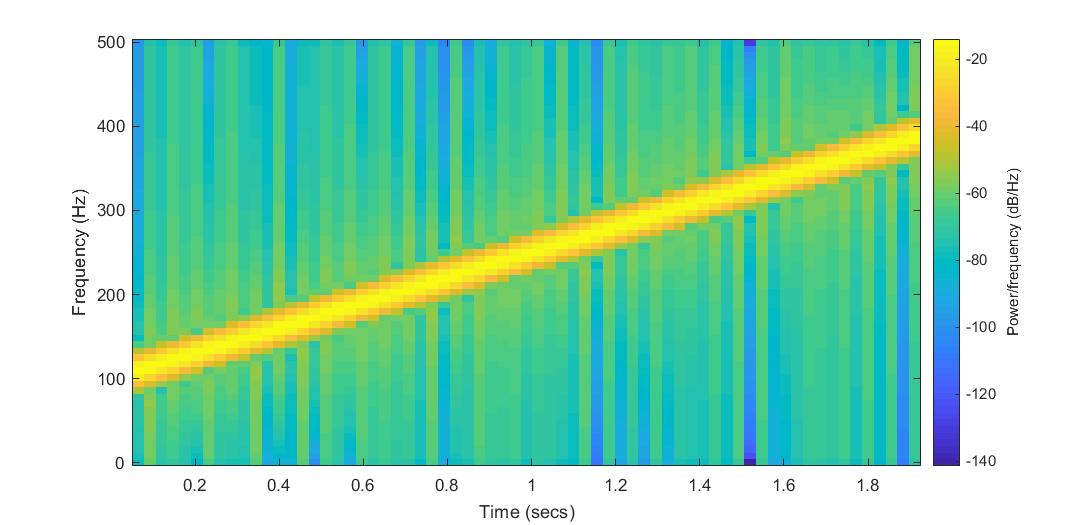
取图像中每一列的最大值，作出图像：

[~,f,t,p] = spectrogram(y,128,100,128,1e3,'yaxis');
[fridge,~,lr] = tfridge(p,f);
plot3(t,fridge,abs(p(lr)),'LineWidth',4)
t(1),fridge(1) %第一个点的坐标
t(end),fridge(end) %最后一个点的坐标

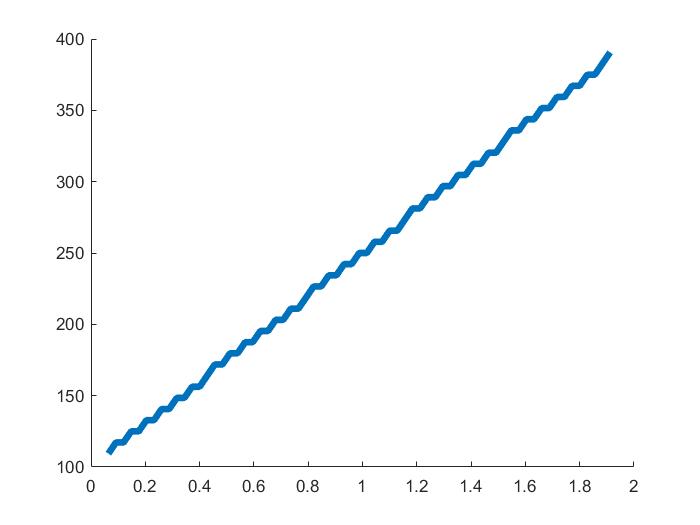
stft最大值

图中，首尾的坐标为：$(0.064, 109.375)$，$(1.912,390.625)$，可以估算出斜率为：$\frac{390.625-109.375}{1.912-0.064}=152.1916$，实际的斜率为 $\frac{400-100}{2-0}=150$，误差为 $1.46\%$

通过上面的实验，STFT 法简单易用，但存在两个困难：1. 窗函数的选择；2. 窗长度的选择。根据 Heisenberg 测不准原则，信号的时/频分辨力不能同时提高。

实验心得

通过 matlab 实验，加深了对几种滤波器设计方法的了解。同时，粗略地了解了利用 STFT 进行参数估计的方法。

参考

上篇变换域中的LTI系统

下篇数字滤波器的结构与实现