线性相位 FIR
前面说过,零相位系统的时域响应以 n=0 对称,如果我们将它进行平移,DTFT频率上对应一个频移,就会得到线性相位 FIR
设 $N+1$ 长的 FIR 滤波器为:
\[H(z)=\sum_{n=0}^N h[n]z^{-n}\]设频率响应为:
\[H(e^{}j\omega)=|H(e^{j\omega}| e^{j\phi(\omega)}\]因为是线性相位,所以 $\phi(\omega)=-\alpha \omega + \beta$,其中 $\alpha$ 是时延因子
从而:
\[\begin{aligned} |H(e^{j\omega}|&=H(e^{}j\omega) e^{-j\phi(\omega)}\\ &=\sum_{n=0}^N h[n] e^{-j[(n-\alpha)\omega+\beta]} \end{aligned}\]上式中的虚部为0,所以:
\[\sum_{n=0}^N h[n] \sin[(\alpha-n)\omega-\beta]=0\]上面有点复杂,为了简化分析,我们不妨这样考虑:$\sin$ 是奇/偶函数,则$h[n]$是偶/奇函数就能让上式为0.
所以我们有两种情况:
- $h[n]$ 为偶,$\sin$ 为奇
- $h[n]=h[N-n]$
- $\beta=0,\alpha=\frac{N}{2}$
- $h[n]$ 为奇,$\sin$ 为偶
- $h[n]=-h[N-n]$
- $\beta=\frac{\pi}{2},\alpha=\frac{N}{2}$
另外,由于 $h[n]$ 的长度可以是奇数或偶数,所以一共有 4 种类型:
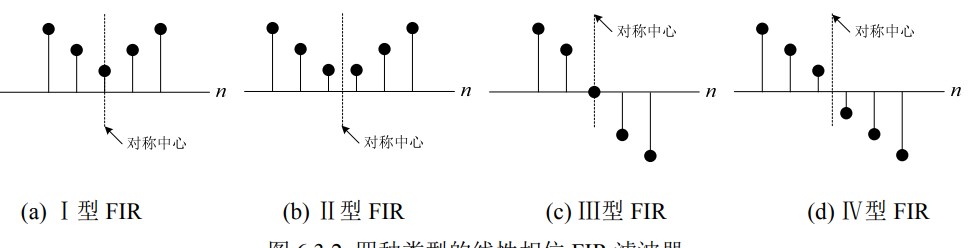
Ⅰ型 FIR 传输函数
- 奇数长度,偶对称
- $\vert H(e^{j\omega})\vert =h[\frac{N}{2}]+2 \sum_{n=0}^{N/2-1}h[\frac{N}{2}-n]\cos(\omega n)$
- $\theta=-\frac{N}{2}\omega+\beta,\beta=0,\pi$
- $\tau_g(\omega)=\frac{\dif \theta(\omega)}{\dif \omega}=-N/2$
Ⅱ型 FIR 传输函数
- 偶数长度,偶对称
- $\vert H(e^{j\omega})\vert =2 \sum_{n=0}^{(N+1)/2}h[\frac{N+1}{2}-n]\cos(\omega (n-\frac{1}{2})$
- $\theta=-\frac{N}{2}\omega+\beta,\beta=0,\pi$
- $\tau_g(\omega)=\frac{\dif \theta(\omega)}{\dif \omega}=-N/2$
Ⅲ型 FIR 传输函数
- 奇数长度,奇对称
Ⅳ型 FIR 传输函数
- 偶数长度,奇对称
线性相位 FIR 的零极点
偶对称的多项式满足:$H(z)=z^{-N}H(z^{-1})$,称为 镜像多项式
奇对称的多项式满足:$H(z)=-z^{-N}H(z^{-1})$,称为 镜像多项式
根据上两式,若 $\xi_0$ 是一个零点,则 $1/\xi_0$ 也是零点。又因为实冲激响应的滤波器的零点以复共轭的方式出现,所以下面四个零点一起出现:
\[r e^{\pm j \phi} \quad \frac{1}{r} e^{\pm j \phi}\]- 当零点在单位圆上时,只有两个。
- 当零点在实轴上时,也只有两个。
- 当零点在 $z=\pm 1$ 时,只有一个零点。(另外,偶数个 $z=1$ 对应镜像多项式,奇数个对应反镜像多项式;$z=-1$ 对应镜像多项式)
而要产生 $k$ 个零点,就要有 $k$ 阶的多项式,反之亦然。注意到上面的零点组合中,只有 $z=\pm 1$ 是奇数。
那么我们说这些废话和 FIR 有什么关系呢?还记得上面的四种 FIR 的长度吗?我们可以从长度知道它们的零点组合:
- Ⅰ型 FIR——奇数长,偶数阶,镜像多项式
- 在 $z=+ 1$ 有偶数个零点,或没有
- 在 $z=- 1$ 有偶数个零点,或没有
- Ⅱ型 FIR——偶数长,奇数阶,镜像多项式
- 在 $z=+1$ 有偶数个零点,或没有
- 在 $z=-1$ 有奇数个零点
- Ⅲ型 FIR——奇数长,偶数阶,反镜像多项式
- 在 $z=+ 1$ 有奇数个零点
- 在 $z=- 1$ 有奇数个零点
- Ⅳ型 FIR——偶数长,奇数阶,反镜像多项式
- 在 $z=+ 1$ 有奇数个零点
- 在 $z=- 1$ 有偶数个零点,或没有
那么,知道了零点对我们的设计有什么用呢?因为 $z=1$ 的零点对应低频 $\omega=0$,$z=-1$ 的零点对应高频 $\omega=\infty$。所以凡是在这些地方有零点的,这部分频率就是阻带。所以,四种 FIR 中不能设计某些滤波器:
- Ⅰ型 FIR:任何滤波器
- Ⅱ型 FIR:不能设计高通
- Ⅲ型 FIR:不能设计低通、高通、带阻
- Ⅳ型 FIR:不能设计低通
设计 FIR 滤波器
窗函数法
窗函数法就是利用一个窗函数+时移,将无穷、非因果的理想滤波器转换为物理可实现的滤波器。加窗的过程如下图所示:
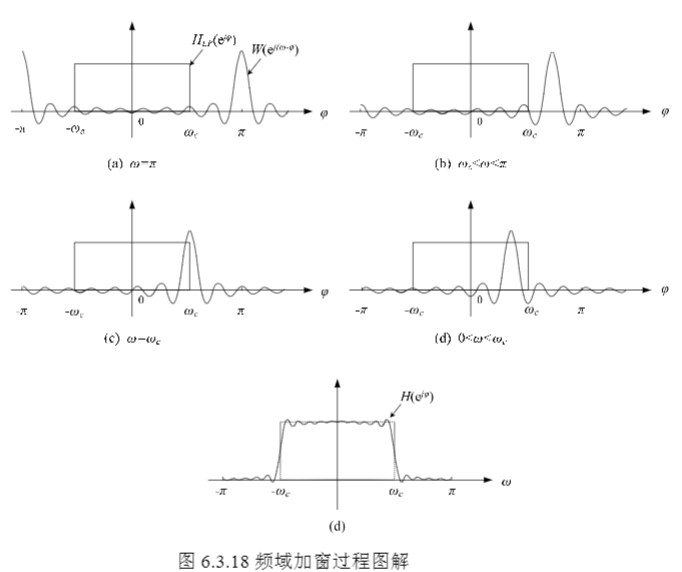
常见的窗函数的特性见下表:
| 窗类型 | 主瓣宽度 | 过渡带宽度 | 相对旁瓣水平 | 最小阻带衰减 |
|---|---|---|---|---|
| 矩形窗 | 4π/(2M+1) | 0.92π/M | -13.3dB | -20.9dB |
| 汉宁窗 | 8π/(2M+1) | 3.11π/M | -31.5dB | -43.9dB |
| 汉明窗 | 8π/(2M+1) | 3.32π/M | -42.7dB | -54.5dB |
| 布莱克曼窗 | 12π/(2M+1) | 5.56π/M | -58.1dB | -75.3dB |
等波纹滤波器法
等波纹最佳逼近法是一种优化设计法,即最大误差最小化准则,它克服了窗函数设计法和频率采样法的缺点,使最大误差(即波纹的峰值)最小化,并在整个逼近频段上均匀分布。用等波纹最佳逼近法设计的FIR数字滤波器的幅频响应在通带和阻带都是等波纹的,而且可以分别控制通带和阻带波纹幅度,这就是等波纹的含义。最佳逼近是指在滤波器长度给定的条件下,使加权误差波纹幅度最小化。与窗函数设计法和频率采样法比较,由于这种设计法使滤波器的最大逼近误差均匀分布,所以设计的滤波器性能价格比最高。阶数相同时,这种设计法使滤波器的最大逼近误差最小,即通带最大衰减最小,阻带最小衰减最大;指标相同时,这种设计法使滤波器阶数最低。
等波纹最佳逼近法的设计思想:用 $H_d(\omega)$ 表示希望逼近的幅度特性函数,要求设计线性相位FIR数字滤波器时,$H_d(\omega)$ 必须满足线性相位约束条件。用 $H(\omega)$ 表示实际设计的滤波器的幅度特性函数。定义加权误差函数$\varepsilon(\omega)$为:
\[\varepsilon(\omega)=W(\omega)[H_d(\omega)-H(\omega)]\]式中,$W(\omega)$ 为幅度误差加权函数,用来控制不同频带(一般指通带和阻带)的幅度逼近精度。等波纹最佳逼近法的设计在于找到滤波器的系数向量 $h[n]$,使得在通带和阻带内的最大绝对值幅度误差 $\vert \varepsilon(\omega)\vert$为最小,这也就是最大误差最小化问题。
习题
10.17(a) 设计低通 FIR 滤波器,指标为 $\omega_p=0.42\pi$,$\omega_s=0.58\pi$,$\delta_p=0.002$,$\delta_s=0.008$,要求长度尽可能小。
解:
$$
\Delta \omega = \omega_s-\omega_p = 0.16\pi\\
\alpha_s = -20 \lg \delta_s=41.93 \text{dB}
$$
选择汉宁窗,$M=\dfrac{3.11\pi}{0.16 \pi} \approx 20$
10.18 设计带通 FIR 滤波器,指标为:
$$
\omega_{p1} = 0.4 \pi \quad \omega_{p2}=0.55\pi\\
\omega_{s1}=0.25\pi \quad \omega_{s1}=0.75\pi\\
\delta_p = 0.022\\
\delta_{s1}=0.006 \quad \delta_{s2}=0.008
$$
解:总之就是取更苛刻的指标来设计窗,具体原理不太理解。
$$
\Delta \omega_1 = \omega_{p1} - \omega_{s1}=0.15\pi\\
\Delta \omega_2 = \omega_{p2} - \omega_{s2}=0.2\pi\,\;\\
\alpha_{s1}=-20 \lg \delta_{s1}=44.43\text{dB}\\
\alpha_{s2}=-20 \lg \delta_{s2}=41.93\text{dB}
$$
以 $\Delta \omega_1$ 和 $\alpha_{s1}$ 作为指标,则选取 Hann 窗,$M=\frac{3.11\pi}{0.15 \pi}\approx 21$
以下是我上学期与下学期写的一些笔记,请老师斧正。