从这章开始,我们正式来研究系列~🧐我们会从一些特殊的系统开始入手,然后进入FIR、IIR,最后实现低通、高通、带通、带阻系统。
幅度!
理想滤波器
如果幅度响应要么是 1,要么是 0,那么就得到我们的四种理想滤波器:
- 理想高通
- 理想低通
- 理想带通
- 理想带阻
这些理想滤波器都是 IIR,非因果,不可实现的。比如最简单的理想低通滤波器,它的冲激响应为:
\[h_\text{LP} [n] = \frac{\sin \omega_c n}{\pi n}, -\infty< n <+\infty\]有界实传递函数
如果幅度响应都不大于 1,那么就得到 有界实传递函数:
\[|H(e^{j\omega})| \leq 1, 对\omega的所有值\]由于这个滤波器的输出信号能量不大于输入信号能量,所以也叫 无源系统。显然,任意稳定的实系数传递函数都能缩放为一个有界实传递函数。
全通传递函数
如果幅度响应对任何频率都是 1,那么就是 全通传递函数:
\[|A(e^{j\omega})|^2 = 1, 对所有 \omega\]其实不一定是 1,只要是个常数即可。另外定义中的平方也是多余的。
为了求全通传递函数的表达式,我们先假设它是一阶系统:
\[A(z)=\frac{\alpha-\beta z^{-1}}{1-\lambda z^{-1}}\]因为是全通函数,所以有:
\[|\alpha-\beta e^{-j\omega}|=|1-\lambda e^{-j\omega}|\]平方后展开(也可以利用余弦定理?),有:
\[\begin{aligned} &\alpha_\text{re}^2+\alpha_\text{im}^2+\beta_\text{re}^2+\beta_\text{im}^2-2(\alpha_\text{re}\beta_\text{re}+\alpha_\text{im}\beta_\text{im})\cos \omega - 2(\alpha_\text{re}\beta_\text{im}-\alpha_\text{im}\beta_\text{re})\sin \omega\\ =&1+\lambda_\text{re}^2+\lambda_\text{im}^2-2 \lambda_\text{re}\cos \omega-2\lambda_\text{im}\sin\omega \end{aligned}\]比较等号两边,有:
\[\begin{cases} \alpha_\text{re}^2+\alpha_\text{im}^2+\beta_\text{re}^2+\beta_\text{im}^2 = 1+\lambda_\text{re}^2+\lambda_\text{im}^2\\ \alpha_\text{re}\beta_\text{re}+\alpha_\text{im}\beta_\text{im}=\lambda_\text{re}\\ \alpha_\text{re}\beta_\text{im}-\alpha_\text{im}\beta_\text{re}=\lambda_\text{im} \end{cases}\]这个太复杂了,直接试一下令 $\alpha=\pm1$ 或 $\beta=\pm1$ 吧,这样可以试出两组解:
\[\begin{cases} \alpha=1\\ \beta=\lambda \end{cases} \text{ or } \begin{cases} \alpha=-\lambda^*\\ \beta=-1 \end{cases}\]对应的全通传递函数为:
\[H(z)=\frac{1-\lambda z^{-1}}{1-\lambda z^{-1}}\\ \text{or}\\ H(z)=\frac{-\lambda^*+z^{-1}}{1-\lambda z^{-1}}\]上面那个分子分母通分后为1,是一个 0阶系统,所以舍去,取下面那个。所以一阶全通传递函数的标准形式是:
\[A(z)=\pm \frac{-\lambda^*+z^{-1}}{1-\lambda z^{-1}}\]注意到这个传递函数的零极点为:
\[极点:\lambda=re^{j\varphi}\\ 零点:\frac{1}{\lambda^*}=\frac{1}{r} e^{j\varphi}\]从式中可以看出:全通传递函数的零点与极点关于单位圆对称。这个对任意 M 阶全通传递函数都成立。
将多个一阶串联,可以得到 M 阶全通传递函数:
\[\begin{aligned} A_M(z)&=\pm \prod_{i=1}^M A_{1,i} (z)\\ &=\pm \prod_{i=1}^M \left( \frac{-\lambda_i^*+z^{-1}}{1-\lambda_i z^{-1}} \right)\\ &=\pm \frac{d_M+d_\text{M-1}z^{-1}+\cdots+d_1 z^{-M+1}+z^{-M}}{1+d_z z^{-1}+\cdots+d_{M-1}z^{-M+1}+d_M z^{-M}} \end{aligned}\]展开后由于要求系数是实数,所以共轭关系就不见了。最后得到的分式中,分子和分母呈镜像多项式,即分子的第 $i$ 项系数对应分母的第 $M-i$ 项系数。
某个全通系统的零极点图如下:
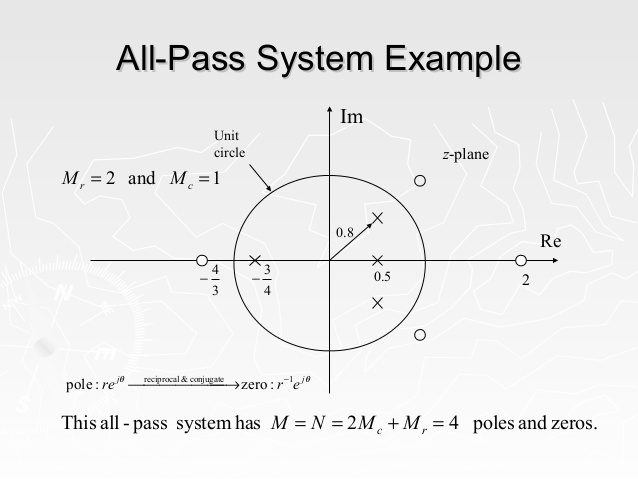
最后我们来稍微考虑一下全通系统的相位函数。先给出结论:
- 全通系统展开后的相位函数单调递减
- $\omega$ 从 0 变化到 $\pi$,$M$ 阶全通函数变化了 $M\pi$ 弧度
课本上的证明很简略(因为这个证明的计算过程很复杂),我这里提供一种“通俗”的证明。我们仅考虑一个一阶全通系统,其零极点在实轴上,并且极点接近 0,零点接近 $\infty$。想象一个点在单位圆上逆时针转动,根据前一章的知识,其相位可以表示为:
\[\theta(\omega)=\arg (e^{j\omega}-\xi)-\arg (e^{j\omega}-\lambda)\]显然,在逆时针转动过程中,零点项几乎不变,而极点项不断的减小,故整体相位是递减的,并且从 $0$ 到 $\pi$ 变化了 $\pi$ 幅度。而串联系统的相位是相加的,所以 $M$ 阶全通传递函数的相位也是递减的,并且从 $0$ 到 $\pi$ 变化了 $M\pi$ 幅度。
由于全通函数在改变相位的同时不影响幅度,我们可以利用全通滤波器来调整系统的相位,这种用途称为 延迟均衡器
相位!
零相位
信号经过零相位系统后相位不会发生失真,也就是说,频率响应是非负实数。假设 $H(z)$ 是任意一个稳定的系统,在单位圆上无极点,那么可以构造:
\[F(z)=H(z)H(z^{-1})\]在单位圆上,有:$F(e^{j\omega})=H(e^{j\omega})H(e^{-j\omega})$,根据离散傅里叶变换的性质:
\[x^*[n] \leftrightarrow X^*(e^{-j\omega})\\ x[-n] \leftrightarrow X(e^{-j\omega})\]由于系统是实系数系统,即 $x^[n]=x[n]$,从而我们有 $x^[-n]=x[-n]$,经过DTFT后得到:$X^*(e^{j\omega})=X(e^{-j\omega})$
于是我们有 $F(e^{j\omega})=H(e^{j\omega})H^*(e^{j\omega})=\vert H(e^{j\omega}) \vert^2$,这是个非负实数,所以 $F(z)$ 是一个零相位系统。
如果 $z_i$ 是 $F(z)$ 的零点/极点,则 $z_i^{-1}$ 也是其零点/极点。可见,其时域响应以 $n=0$ 对称,所以这是个非因果系统。
要想实现这个系统,只能对有限长输入信号进行非实时处理,也就是说,我们知道整个输入信号,然后我们可以用如下方式处理:
- 将信号通过一个因果实系数滤波器 $H(z)$,得到 $X(e^{j\omega})H(e^{j\omega})$
- 将 1. 中输出信号时间反转,得到 $X(e^{-j\omega})H(e^{-j\omega})$
- 将 2. 中输出信号再次输入到 $H(z)$,得到 $X(e^{-j\omega})H(e^{-j\omega})H(e^{j\omega})$
- 将 3. 中输出信号时间再次反转,得到最终输出信号 $X(e^{j\omega})H(e^{j\omega})H(e^{-j\omega})=X(e^{j\omega})\vert H(e^{j\omega}) \vert^2$
另一种方法是先反转、再滤波、再反转、再滤波,效果也是一样的。此外,还有一种并联的方案:
- 一路信号直接滤波,得到 $X(e^{j\omega})H(e^{j\omega})$
- 一路信号经过时反、滤波、时反,得到 $X(e^{j\omega})H(e^{-j\omega})$
- 将两路信号相加,得到 $X(e^{j\omega})[H(e^{j\omega})+H(e^{-j\omega})]=X(e^{j\omega})[H(e^{j\omega})+H^*(e^{j\omega})]$
线性相位
线性相位 即输出是输入的延时信号:
\[\begin{aligned} y[n]&=x[n-D]\\ Y(e^{j\omega})&=e^{-j\omega D} X(e^{j\omega})\\ H(e^{j\omega})&=e^{-j\omega D} \end{aligned}\]该频率响应具有单位幅度响应,对所有频率的群延时均为 D. 我们可以将要求放宽一点,只需要在通带内线性相位即可,阻带内相位随意:

最小相位与最大相位
一个无脑的定义就是:
- 所有零点在单位圆内的因果稳定传输函数称为 最小相位传输函数
- 所有零点在单位圆外的因果稳定传输函数称为 最大相位传输函数
- 内外都有零点的称为 混合相位传输函数
然后一个结论是:
- 仅当一个因果离散时间系统具有最小相位传输函数,可以设计出该因果离散时间系统的一个稳定逆函数,且逆系统也是最小相位系统。(因为逆系统的极点对应原系统零点)
记住上面的东西就差不多了。不过想要知道为什么叫「最小相位」,请往下看。
“最小”相位指的是:在幅度响应相同的因果稳定系统中,最小相位系统的群延时最小。证明如下:
假设 $H(z)$ 中的一个零点 $a$ 在单位圆内,则它对相位的贡献为:
\[\begin{aligned} \varphi_a(\omega)&=\arg \left( 1-ae^{-j\omega}\right)\\ &=\arg \left( 1- |a|e^{j\theta_a} e^{-j\omega} \right)\\ &=\arg \left( 1- |a|e^{-j(\omega-\theta_a)} \right)\\ &=\arg \big\{ 1- |a| \cos(\omega-\theta_a) + j|a| \sin(\omega-\theta_a) \big\}\\ &=\arg \big\{ |a|^{-1}-\cos(\omega-\theta_a) + j\sin(\omega-\theta_a) \big\} \end{aligned}\]群延时为:
\[-\frac{\dif \varphi_a(\omega)}{\dif \omega} = \frac{|a|-\cos(\omega-\theta_a)}{|a|+|a|^{-1}-2\cos(\omega-\theta_a)}\]对幅度响应的贡献为:
\[|1-a e^{-j\omega}|^2= 1 -2|a| \cos(\omega-\theta_a)+|a|^2\]如果将 $a$ 移到圆外,也就是替换为 $(a^{-1})^*$($\vert a \vert \rightarrow \dfrac{1}{\vert a \vert}$,$\theta_a$ 不变),那么对幅度响应的贡献变为:
\[|1-a e^{-j\omega}|^2= \frac{1}{|a|^2}[1 -2|a| \cos(\omega-\theta_a)+|a|^2]\]由于只是缩放了一个常数,可以通过常数项补回来。对群延时的贡献为:
\[-\frac{\dif \varphi_a(\omega)}{\dif \omega} = \frac{|a|^{-1}-\cos(\omega-\theta_a)}{|a|+|a|^{-1}-2\cos(\omega-\theta_a)}\]对比发现,群延时的分子部分增大了($\vert a \vert<1$),说明群延时增大了。对应的相位响应如下:
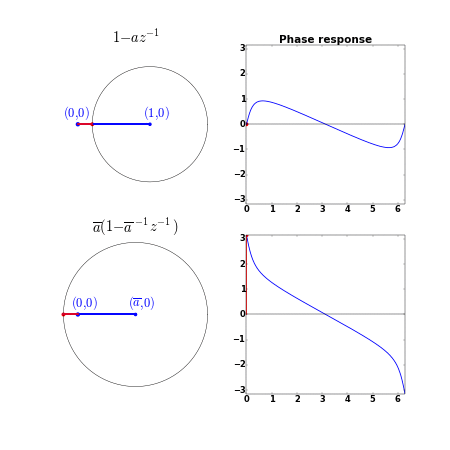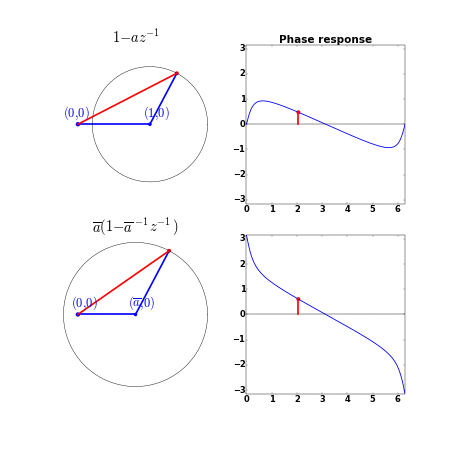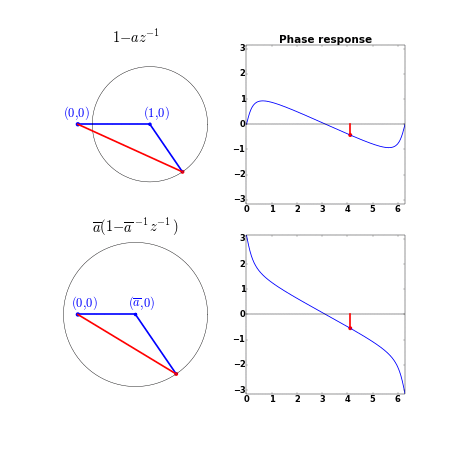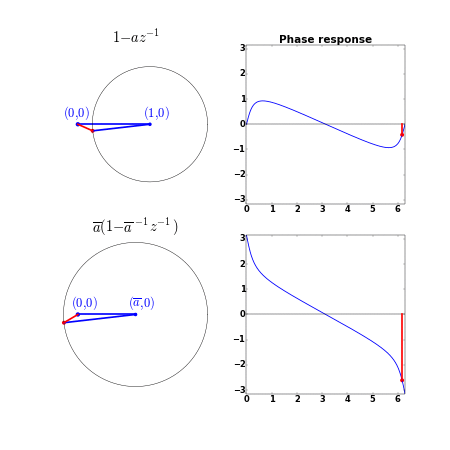
如果有 $N$ 个零点,那么,这 $N$ 个零点都在圆内时的相位最小(相位是群延时的累积),当我们依次将零点移到圆外时,相位增大,当所有零点都在圆外时,相位最大。这就是最小相位与最大相位的由来。
互补!
上面只是单个传递函数,下面我们来考虑多个传递函数之间的关系。
延时互补
\[\sum_{k=0}^{L-1} H_k(z)=\gamma z^{-n_0},\; \gamma\neq 0\]全通互补
\[\sum_{i=0}^{M-1} H_i(z)=A(z)\]功率互补
\[\sum_{i=0}^{M-1} |H_i(e^{j\omega})|^2=K\]双互补
即全通互补,又功率互补。
习题
7.22 考虑两个因果 LTI 系统:$h_1[n]=\alpha\delta[n]+\beta\delta[n-1]$ 和 $h_2[n]=\gamma^n \mu[n]$,$\vert \beta \vert <1$ 的级联,求整个系统的频率响应 $H(e^{j\omega})$,当 $\alpha$,$\beta$ 和 $\gamma$ 取什么值时,该系统是一个幅度响应为 $K$ 全通系统。
解:对系统函数进行 z 变换:$H_1(z)=\alpha+\beta z^{-1}$,$H_2(z)=\dfrac{1}{1-\gamma z^{-1}}$,级联后为 $H(z)=\dfrac{\alpha+\beta z^{-1}}{1-\gamma z^{-1}}$
令 $z=e^{j\omega}$,则频率响应为 $H(e^{j\omega})=\dfrac{\alpha+\beta e^{-j\omega}}{1-\gamma e^{-j\omega}}$
因为一阶全通函数具有如下形式:$H(z)=K\frac{-\lambda^*+z^{-1}}{1-\lambda z^{-1}}$,故 $\alpha,\beta,\gamma$ 满足:
$$
\begin{cases}
\alpha = -\lambda^* \cdot K\\
\beta = 1\\
\gamma = \lambda
\end{cases}\\
\lambda \in \mathbb{C}
$$
或更简单的,可以令 $\alpha=K,\beta=-K\gamma,\gamma\in \mathbb{C}$
7.30 二型线性相位 FIR 滤波器的传输函数为:
$$
H_1(z) = 2.5+0.5 z^{-1}+0.35 z^{-2}+5.47 z^{-3}+5.47 z^{-4}+0.35z^{-5}+0.5 z^{-6}+2.5 z^{-7}
$$
- 求相同幅度响应的最小相位 FIR 系统
- 求相同幅度响应的最大相位 FIR 系统
- 求相同幅度响应的混合相位 FIR 系统
- 上述系统一共有多少个
解:就是移动零点。假设一个零点为 $a$,那么将它替换成 $(a^{-1})^*$,再对系统乘上一个 $\vert a\vert^2$ 的话,不会改变幅度响应。
所以本题的重点在于求解零点,7阶系统一共有 7 个零点,并且满足二型 FIR 的特点。我们可以利用 MATLAB 求解,解出:
$$
\begin{cases}
a_1= 0.8000 + 1.1662j\\
a_2= 0.8000 - 1.1662j\\
a_3=-1.0000 + 0.0000j\\
a_4=-0.8000 + 0.6000j\\
a_5=-0.8000 - 0.6000j\\
a_6= 0.4000 + 0.5831j\\
a_7= 0.4000 - 0.5831j\\
\end{cases}
$$
离原点的距离为:
$$
\begin{cases}
a_1=a_2=1.4142\\
a_3=a_4=a_5=1\\
a_6=a_7=0.7071
\end{cases}
$$
$a_3,a_4,a_5$ 已经在圆上了,我们只能移动 $a_1,a_2,a_3,a_4$. 由于不要求是线性相位,所以可以只移动单个零点。所以:
- $H_2(z)=\vert a_1\vert^2 \vert a_2 \vert^2(1-(a_1^{-1})^*z^{-1})(1-(a_2^{-1})^*z^{-1})(1-a_3z^{-1})(1-a_4z^{-1})(1-a_5z^{-1})(1-a_6z^{-1})(1-a_7z^{-1})$
- $H_3(z)=\vert a_6\vert^2 \vert a_7 \vert^2(1-a_1z^{-1})(1-a_2z^{-1})(1-a_3z^{-1})(1-a_4z^{-1})(1-a_5z^{-1})(1-(a_1^{-1})^*z^{-1})(1-(a_2^{-1})^*z^{-1})$
- 有多个,只写其中一个:$H_4(z)=\vert a_1\vert^2(1-(a_1^{-1})^*z^{-1})(1-a_2z^{-1})(1-a_3z^{-1})(1-a_4z^{-1})(1-a_5z^{-1})(1-a_6z^{-1})(1-a_7z^{-1})$
- $2^4-1=15$ 种
7.39 1型实系数 FIR 滤波器具有如下零点:$z_1=1$,$z_2=-0.6$,$z_3=-1+j$,求剩余零点并写出传输函数
解:容易求出 $z_2,z_3$ 各自对应的其他零点:
$$
z_2 \rightarrow \frac{1}{z_2}\\
z_3 \rightarrow \frac{1}{z_3},z_3^*,\frac{1}{z_3^*}
$$
由于 1 型 FIR 是镜像多项式,所以在 $z=1$ 处至少有 2 个零点。故可以写出其传输函数为:
$$
\begin{aligned}
H(z)=&(1-z^{-1})^2(1+0.6z^{-1})(1+\frac{1}{0.6}z^{-1})(1+(-1+j)z^{-1})(1+(-1-j)z^{-1})
\\&(1+\frac{1}{-1+j}z^{-1})(1+\frac{1}{-1-j}z^{-1})
\end{aligned}
$$
7.54 设 $P(z)$ 和 $Q(z)$ 是次数为 $N$ 和 $M$ 的两个反镜像多项式,且 $M=N-2R$,证明:$X(z)=P(z)+z^{-R}Q(z)$ 是一个次数为 $N$ 的反镜像多项式
解:只需证:$X(z)=-z^{-N} X (z^{-1})$
$$
\\
\begin{aligned}
-z^{-N} X (z^{-1}) &= -z^{-N} P(z^{-1})-z^{-N+R} Q(z^{-1})\\
&=P(z)+z^{M-N+R} Q(z)\\
&=P(z)+z^{N-2R-N+R} Q(z)\\
&=P(z)+z^{-R} Q(z)\\
&=X(z)
\end{aligned}
$$