结构单元
框图
框图啥的就不再介绍了,简单来说,咱们只能用三种结构:加(⊕)、数乘(▷p)和单位延迟($z^{-1}$)
无延迟回路
无延迟回路 指的是没有任何延时的反馈回路。一种简单的判断方法是:从输出反馈出发,经过一个环回到反馈,环路上没有延迟的话,就是无延迟回路。
无延迟回路在物理中是不可实现的,但我们能改变它的结构,使其变为有延迟回路。因为无延迟回路总能写成:
\[y[n]=Ay[n]+x[n]\]显然,可以改写成 $y[n]=x[n]/(1-A)$
典范结构
典范结构(规范结构):滤波器的延时单元数目与差分方程的阶数($\max(M,N)$)相同的框图。反之,若延迟单元大于阶数,则称为非典范结构
等效结构
若两个框图对应的传输函数相同,则称为它们是 等效的。要得到等效结构,一种方法叫 转置运算,步骤如下:
- 将所有箭头反转
- 把节点换成加法器,加法器换成节点
- 交换输入和输出
由于计算机的精度有限,所以等效结构存在性能区别:
- 所需的存储单元和乘法次数不同,前者影响复杂度,后者影响运算速度
- 有限精度下,不同结构的误差和稳定性不同
系统的基本实现
串联实现
一个数字滤波器可以实现,它的传输函数的分子、分母多项式必须是实系数的。而实系数多项式的根只有实数和共轭复数两种情况,因为:
\[\text{if}\quad \sum_{k=0}^{m} b_k z^{-k}=0\\ \text{then}\quad \sum_{k=0}^{m} b_k (z^*)^{-k}=0\]我们可以将高阶系统因式分解为多个一阶系统和二阶系统的串联,其中,一阶系统提供 $N-2r$ 个实根,二阶系统用于提供 $r$ 对实根和共轭根,即
\[H(z)= \rho_0 \left(\prod_{i=1}^{r} \frac{1+\beta_{1i} z^{-1}+\beta_{2i}z^{-2}}{1+\alpha_{1i}z^{-1}+\alpha_{2i}z^{-2}}\right) \left(\prod_{i=1}^{N-2r} \frac{1+\gamma_i z^{-1}}{1+p_i z^{-1}} \right)\]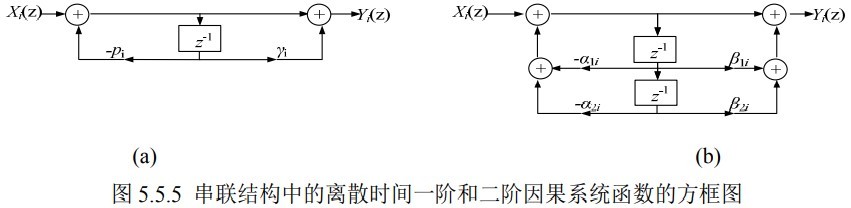
如果高阶多项式的最高阶数为偶数,则因式分解后的实系数多项式最小阶数可能为 1,也可能为 2;若高阶多项式的最高阶数为奇数,则因式分解后的实系数多项式最小阶数为 1。
串联实现的好处是:可以降低滤波器系数的量化误差。
并联实现
好像要根据留数展开来分解,有点复杂,简而言之就是分解后,分母阶数要大于分子:
\[H(z)=\frac{b_0}{a_0}+\sum_{i=1}^r \frac{\beta_{1i}+\beta_{2i}z^{-1}}{1+\alpha_{1i}z^{-1}+\alpha_{2i}z^{-2}}+\sum_{i=1}^{N-2r} \frac{\gamma_i}{1+p_iz^{-1}}\]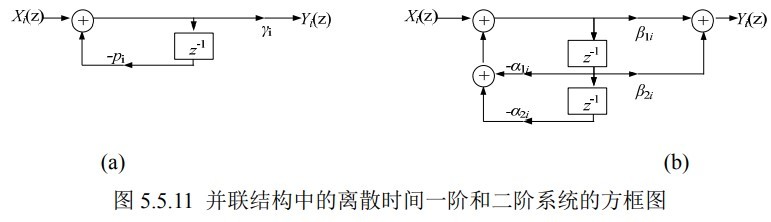
如果有多重根,第 k 个重根 $H_{ik}(z)=\dfrac{\gamma_{ik}}{(1+p_i z^{-1})^k}$ 可以通过级联来实现:

但这样的话,m 重实根就需要 $(1+2+\cdots+m)$ 个一阶节来实现,这并不经济。实际上我们可以用下面结构来表示:
\[H_i(z)=\sum_{k=1}^m \frac{\gamma_{ik}}{(1+p_i z^{-1})^k}\]
FIR
考虑一个 FIR 系统:
\[y[n]=\sum_{k=0}^{M} p_k x[n-k]\]我们可以先延迟,再乘系数,得到如下 直接型实现:
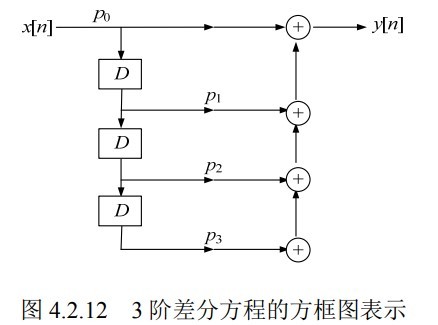
或者先乘系数,再延迟,得到另一种直接型实现(也可以看作是上一种实现的转置):
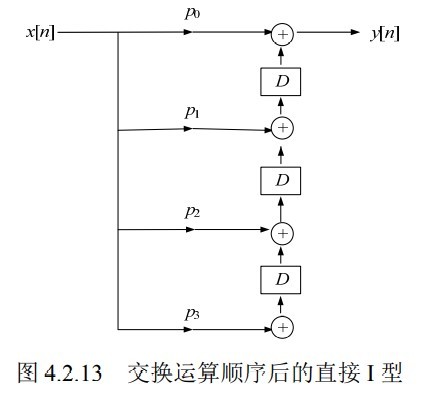
IIR
考虑一个 IIR 系统:
\[\sum_{k=0}^N d_k y[n-k]=\sum_{k=0}^M p_k x[n-k]\]它可以重新写成这种结构:
\[y[n]=\sum_{k=0}^M p_k x[n-k] - \sum_{k=1}^N d_k y[n-k]\]显然右边可以看作是两个 FIR 相加,所以我们可以得到 直接Ⅰ型 实现:
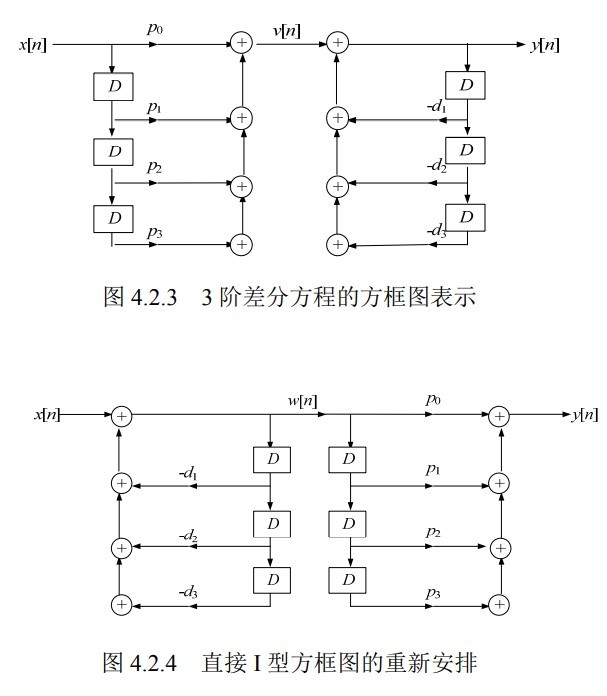
由于串联结构的顺序可以调换,所以我们可以得到上图4.2.4的结构。
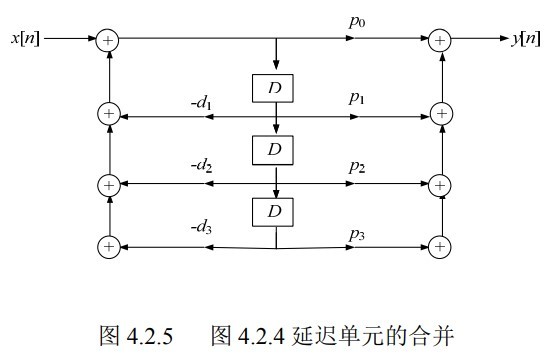
注意到上面两派的延迟的输入是一样的,所以我们可以合并,得到直接Ⅱ型 实现:
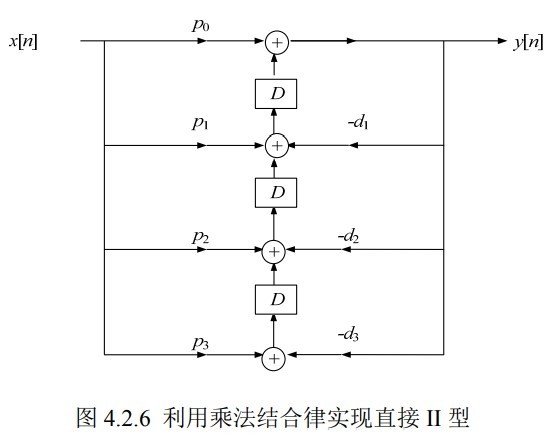
经过转置后可以得到下面的结构:
两类实现的比较:
| 直接Ⅰ型 | 直接Ⅱ型 | |
|---|---|---|
| 加法器 | $N+M$ | $N+M$ |
| 乘法器 | $N+M+1$ | $N+M+1$ |
| 延时器 | $N+M$ | $\max{M,N}$ |
习题
8.28 将下面三个因果一阶 LTI 系统级联:
$$
H_1(z)=\frac{1-0.6z^{-1}}{1+0.25z^{-1}}\\
H_2(z)=\frac{0.2+z^{-1}}{1+0.3z^{-1}}\\
H_3(z)=\frac{2}{1+0.25z^{-1}}
$$
(a)求整个系统的传输函数
(b)求差分方程
(c)每节用直接Ⅱ型,求系统实现
(d)求并联Ⅰ型实现
(e)求冲激响应
解:
$$
H(z)=H_1(z)H_2(z)H_3(z)=\frac{0.4+1.76z^{-1}-1.2z^{-2}}{1+0.8 z^{-1}+0.2125 z^{-2}+0.0187z^{-3}}\\
y[n]+0.8 y[n-1]+0.2125 y[n-2]+0.0187y[n-3]= 0.4x[n] +1.76 x[n-1]-1.2x[n-2]
$$
直接Ⅱ型实现如下:

将系统函数分解为和式:$H(z)=\frac{-676.8}{1+0.3z^{-1}}\frac{548}{1+0.25 z^{-1}}+\frac{129.2}{(1+0.25z^{-1})^2}$,从而可以得到并联Ⅰ型实现如下:
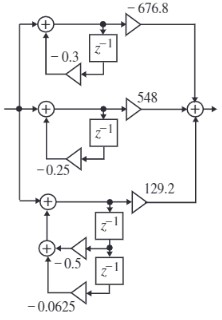
可以求得冲激响应为:
$$
h[n]=-676.8(-0.3)^n u[n]+548(-0.25)^n u[n]+129.2 129.2(n+1)(-0.25)^{(n+1)}u[n]
$$
8.32 下面这玩意是不是典范结构,不是的话就改成典范结构。
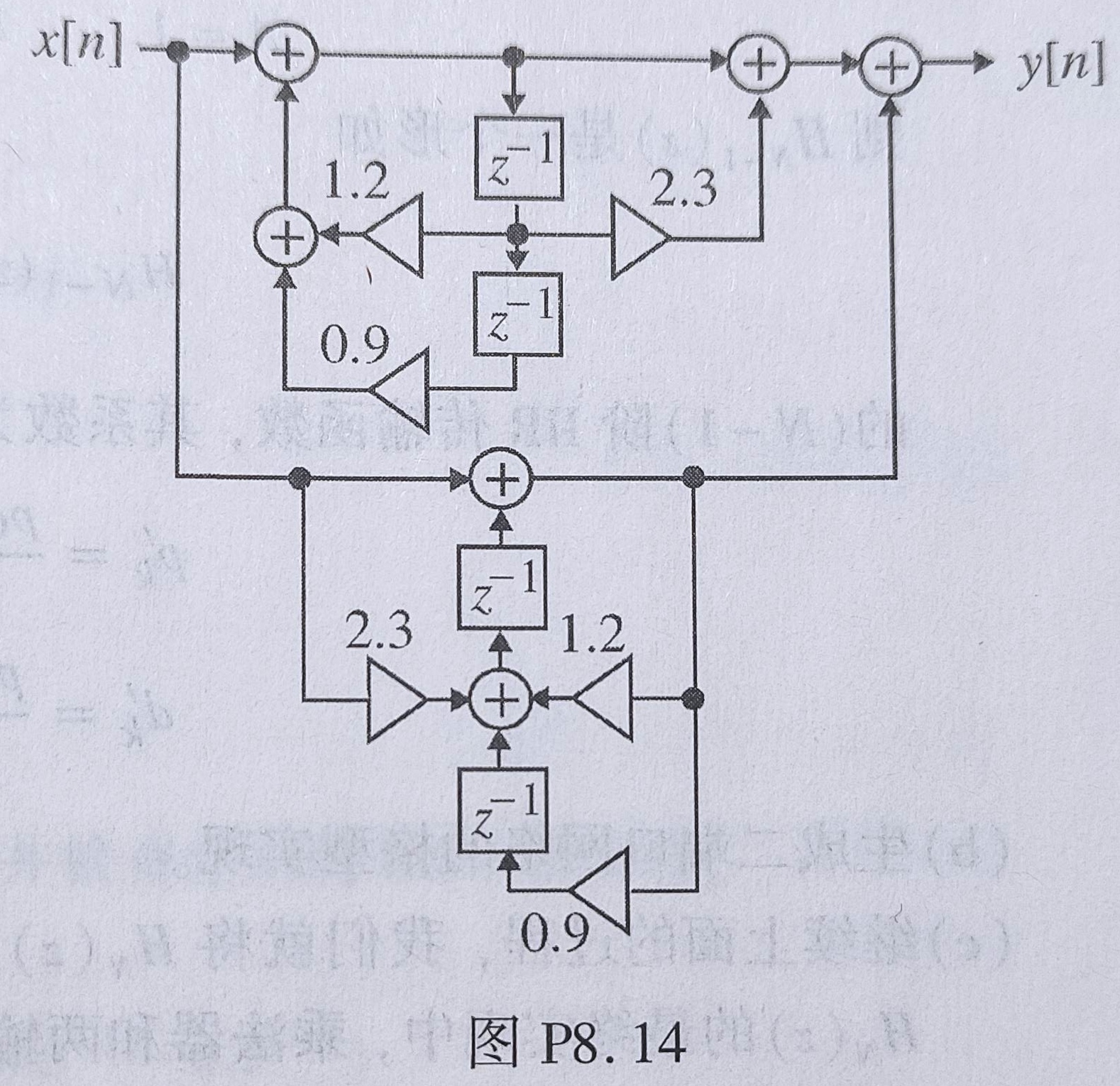
解:这么问肯定就不是啦!容易看出,这是两个子系统并联,并且两个子系统是一样的。所以只需要去掉任意一个,然后在输入或输出处加一个乘 $2$ 即可。