电导的微观理论
欧姆定律的微分形式
\[V=RI=\rho \frac{L}{S} I\Leftrightarrow \begin{cases} J=\frac{I}{S}\\ E=\frac{V}{L}\\ \sigma=\frac{1}{\rho}\\ \end{cases}\\ \Longrightarrow\vec{J}=\sigma \vec{E}\]$\sigma$ 是电导率,与载流子浓度、载流子的迁移率有关(在下一节推导)。
漂移速度和迁移率
电子在外加电场的作用下产生的定向运动称为漂移运动。设 $\bar{v}_d$ 为平均漂移速度,则电流:
\[\begin{align} I&=(-q)n\bar{v}_dS\\ J&=\frac{I}{S}=-nq\bar{v}_d \end{align}\]当电场恒定时,电子具有恒定的平均漂移速度,并且大小与电场强度成正比,可以写为:
\[|\bar{v}_d|=\mu |E|\]$\mu$ 为电子的迁移率,单位为 $\mathrm{cm^2/V\cdot s}$,物理意义表示电子在电场作用下做漂移运动的难易程度。所以:
\[J=nq\bar{v}_d=nq\mu E=\sigma E\\ \sigma=nq\mu\]故电导率与载流子浓度、载流子的迁移率有关
半导体的电导率和迁移率
半导体中存在两种载流子:电子n 与 空穴p,所以有两种迁移率:
\[J=J_n+J_p=(nq\mu_n+pq\mu_p)|E|\\ \sigma=nq\mu_n+pq\mu_p\]- 对于 n 型半导体:$\sigma=nq\mu_n$
- 对于 p 型半导体:$\sigma=pq\mu_p$
- 对于本征半导体:$\sigma_i=n_iq(\mu_n+\mu_p)$,$n=p=n_i$
载流子的散射
由于载流子在半导体中运动时,会与晶格原子与杂质离子发生碰撞,碰撞后载流子速度的大小和方向会改变,用波的概念,就是发生的散射。正是由于碰撞的存在,所以漂移速度并不会无穷增大。
平均自由时间
设 $N_0$ 个电子沿某方向运动,在 $t$ 时刻有 $N(t)$ 个电子未受到散射,单位时间内受到散射的次数为 $P$,则:
\[N(t)P\dif t=N(t)-N(t+\dif t)=-\frac{\dif N(t)}{\dif t}\cdot\dif t\\ \therefore N(t)=N_0\exp(-Pt)\]我们称两次散射之间的时间为平均自由时间(弛豫时间),在 $t$ 时刻,有 $N(t)P\dif t$ 个电子发生散射,则这些散射电子的自由时间就是 $t$,则平均自由时间 $\tau$ 表示为:
\[\tau=\frac{1}{N_0}\int_0^\infty t\cdot PN_0\exp(-Pt)\dif t=\frac{1}{P}\]$\tau$ 的物理意义是,所有电子从 $t=0$ 开始加速自由运动,平均来说 $t=\tau$ 时受到一次散射。
设 $t=0$ 时电子受到一次散射,初速度为 $v_0$,经过 $t$ 后再次散射,散射前的速度为 $v(t)$,则有:
\[v(t)=v_0+\frac{-qE}{m_n^*}t\]对所有电子取平均,初速度为0,故有:
\[\langle v(t) \rangle=\langle v_0 \rangle - \langle \frac{qE}{m_n^*}t \rangle = - \langle \frac{qE}{m_n^*}t \rangle\]从而:
\[\begin{align} \bar{v}_d&=\frac{1}{N_0}\int_0^\infty \left( \frac{-qE}{m_n^*}t \right) PN_0\exp(-Pt)\dif t\\ &=\frac{1}{N_0}\int_0^\infty \left( \frac{-qE}{m_n^*}t \right) \frac{1}{\tau}N_0\exp(-t/\tau)\dif t\\ &=-\frac{qE}{m_n^*}\tau_n\\ &=\mu_n E \end{align}\]所以迁移率的微观表达式为:
\[\mu_n = \frac{q\tau_n}{m_n^*}\\ 同理, \mu_p = \frac{q\tau_p}{m_p^*}\]主要的散射机构
散射的根本原因是周期性势场发生破坏,在附加 $\Delta V$ 的作用下使能带中的电子在不同 $k$ 状态间迁移。下面讨论产生附加势场的原因。
电离杂质散射

如图,在库伦力作用下发生弹性散射,我们有:
\[P_i \propto N_i T^{-3/2}\\ \Rightarrow \tau\propto\frac{T^{3/2}}{N_i}\quad\mu_i\propto\frac{T^{3/2}}{N_i}\]上式说明:
- 杂质浓度越高 $N_i$,散射几率越大;
- 温度越高,载流子平均热运动速度越大,散射几率越小。
比方:警察抓小偷,警察越多,小偷越容易抓到;小偷跑得越快,越不容易被抓住。
晶格振动散射
原子在晶格上振荡,我们将这些振动分解为不同的基本波动按照波的叠加原理组合而成,(就像很多弹簧振子叠加),称为 晶格振动波 或 格波 可分为:
- 声学波(整体)
- 横波
- 纵波
- 光学波(相对)
- 横波
- 纵波
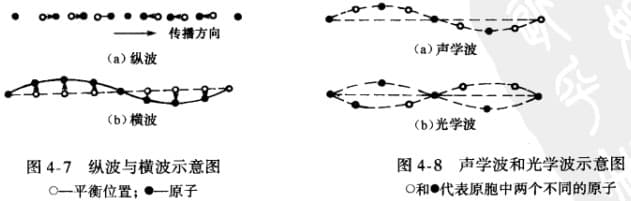
对于频率为 $\omega_q$ 的格波,其平均能量 $\bar{E}$ 和 平均声子数 $\bar{n}$ 为:
\[\bar{E}=\bar{n}\hbar \omega_q = \frac{\hbar\omega_q}{\exp(\hbar\omega_q/kT)-1}\\ \bar{n}=\frac{1}{\exp(\hbar\omega_q/kT)-1}\]声子
我们定义一种准粒子 声子,它既有能量和动量。从而我们将电子受晶格振动的散射,转化为电子与声子的散射。(具体的推导请参考固体物理学)
声子散射遵循能量守恒和动量守恒:
\[\begin{cases} E'-E=\pm\hbar\omega\\ \hbar \vec{k}'-\hbar\vec{k}=\pm\hbar\vec{q} \end{cases}\]$\vec{q}=2\pi/\lambda$ 表示格波的波矢(波长及其传播方向),其能量是量子化的。
声学波散射几率:$P_s \propto T^{3/2}$,$\tau_s \propto T{-3/2}$,$\mu_s\propto T^{-3/2}$
迁移率与浓度、温度的关系
几种散射机构存在时(比如同时有 Si,Ge),$P=P_1+P_2+\cdots$,$\dfrac{1}{\tau}=P=\dfrac{1}{\tau_1}+\dfrac{1}{\tau_2}+\cdots$,$\dfrac{1}{\mu}=\dfrac{1}{\mu_1}+\dfrac{1}{\mu_2}+\cdots$
\[\begin{cases} 电离杂质散射\mu_i=\dfrac{q}{m^*}\dfrac{T^{3/2}}{BN_i}\\ 声学波散射 \mu_s = \dfrac{q}{m^*}\dfrac{1}{AT^{3/2}} \end{cases}\\ \therefore \mu=\frac{q}{m^*}\frac{1}{AT^{3/2}+\frac{BN_i}{T^{3/2}}}\]由公式可以看出,在温度较低时,以电离杂质散射为主,在温度较高时,以声学波散射为主。并且总体是随温度升高,先增加,后减小。
另外,由公式也能看出,当杂质浓度 $N_i$ 越高,电离杂质散射越强,迁移率越低。