\[\newcommand{\dif}{\mathop{}\!\mathrm{d}} \newcommand{\p}{\partial}\]

状态密度

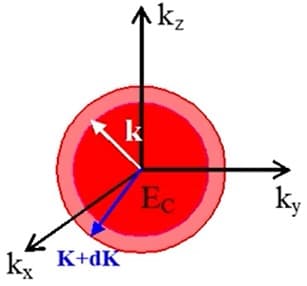
在自由电子费米气体中，我们知道电子在 k 空间是均匀分布的。下面来讨论电子在不同能带中的密度。

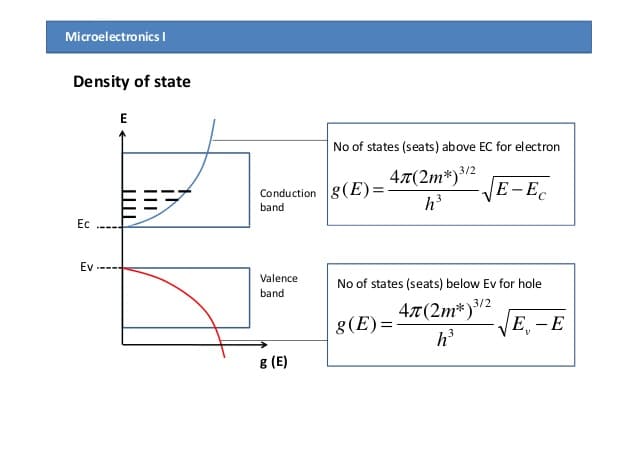
定义 状态密度：单位能量间隔内的状态数目：$g(E)=\dfrac{\dif Z}{\dif E}$

已知 k空间考虑自旋状态密度为：$\dfrac{\dif Z}{\dif \Omega^*}=2/\left( \dfrac{2\pi}{L} \right)^3=\dfrac{2V}{(2\pi)^3}$

将状态密度改写为，$g(E)=\frac{\dif Z}{\dif E}=\frac{\dif Z}{\dif \Omega^*}\frac{\dif \Omega^*}{\dif k}\frac{\dif k}{\dif E}$，注意到第一个分式即 k空间密度，我们只需要求后两项即可。也就是：

\[\dif E \Rightarrow \dif k \Rightarrow \dif \Omega^* \Rightarrow \dif Z\\ 能量\Rightarrow k状态变化 \Rightarrow k空间体积变化 \Rightarrow 状态的变化\]

我们只需要将 $\frac{\dif \Omega^*}{\dif E}$，也就是等能面方程写出来即可。比如：球形等能面导带中的状态密度

\[E-k关系：E(k)=E_c+\frac{\hbar^2k^2}{2m_n^*}\\ 等能面方程：k^2=\frac{(E-E_c)2m_n^*}{\hbar^2}\\ 球体体积：\Omega^*=\frac{4}{3}\pi k^3\\ 从而： \begin{cases} \dif k=\frac{1}{k}\frac{m_n^*}{\hbar^2}\dif E\\ \dif \Omega^*=4\pi k^2\dif k\\ \dif Z=\frac{2V}{(2\pi)^3}\dif \Omega^* \end{cases}\\ \therefore g_c(E)=\frac{\dif Z}{\dif E}=\frac{4\pi V}{h^3}(2m_n^*)^{3/2}(E-E_c)^{1/2}\]

因此，我们得到了导带中的状态密度，这个方程有如下特点：

1. 状态密度与能量呈抛物线关系
2. 有效质量越大，状态密度也就越大
3. 仅适用于能带值附近