倒易点阵 reciprocal lattice

晶体性质的周期性我们可以表示为 $\vec{T} = u \vec{a} + v \vec{b} + w \vec{c}$，这深层次上有如下含义：

1. 在平移操作 $\vec{T}$ 下，晶体的任何物理性质都不变
2. 电荷浓度、电子数密度、质量密度、磁矩密度在 T 作用下不变
3. 电子数密度 $n(r)$ 是 $r$ 的周期函数，存在 $n(\vec{r} + \vec{T}) = n(\vec{r})$

既然这是一个周期函数，就可以用 傅里叶分析。以周期为 $a$ 的一维周期函数 $n(x)$ 为例，将 $n(x)$ 展开为傅里叶级数：

\[n(x) = n_0 + \sum_{p>0} [C_p \cos(2\pi p x/a) + S_p \sin(2\pi p x/a)]\]

其中，$p$ 为正整数；$C_p, S_p$ 为实常数，称为展开式的傅里叶系数。辐角中的 $2\pi /a$ 保证 n(x) 具有周期 a

$2\pi p/a$ 称为晶体的倒易点阵中或傅里叶空间的一个点。$a$ 的量纲为长度，所以 $2\pi p/a$ 的量纲是长度的倒数。这就是 “倒易” 的来源。

我们可以用虚数改写傅里叶级数：

\[n(x) = \sum_p n_p \mathrm{e}^{i 2\pi px/a}\]

其中 $p$ 是全体整数，$n_p$是复数，并且要满足 $\bar{n}_{-p}=n_p$. $2\pi p/a$ 是晶体的倒易点阵中的阵点（p 可正可负），全体点 $\cdots, -4\pi/a, -2\pi/a, 0,$ $2\pi/a, 4\pi/a, \cdots$ 构成了倒易点阵

我们直接将 一维扩展到三维：

\[n(\vec{r}) = \sum_\vec{G} n_\vec{G} \mathrm{e}^{i\vec{G} \cdot \vec{r}}\]

那么 $\vec{G}$ 应该怎么取才满足周期性$n(\vec{r} + \vec{T}) = n(\vec{r})$？这里我们直接给出由 初基 推出倒易点阵的初基矢量

\[\vec{A} = 2\pi \frac{\vec{b}\times \vec{c}}{\vec{a}\cdot\vec{b}\times\vec{c}}\\ \vec{B} = 2\pi \frac{\vec{c}\times \vec{a}}{\vec{a}\cdot\vec{b}\times\vec{c}}\\ \vec{C} = 2\pi \frac{\vec{a}\times \vec{b}}{\vec{a}\cdot\vec{b}\times\vec{c}}\]

由上面三条方程，我们有以下注释：

1. $\vec{A},\vec{B},\vec{C}$ 每个矢量于晶体点阵的两个轴矢量正交
2. 对于给定晶体点阵的一组任一设定的初基矢量 $\vec{a},\vec{b},\vec{c}$ 都能导出一组倒易点阵
3. 每个晶体结构都有两套点阵与之联系，一是晶体点阵，一是倒易点阵
4. 倒易点阵的用处：晶体的衍射图样是晶体的倒易点阵的映像。

我们来验算一下，这样得出的 $\vec{G}$ 是否满足 $n(\vec{r} + \vec{T}) = n(\vec{r})$：

\[\text{设：} \begin{cases} \vec{G} &= h \vec{A} + k \vec{B} + l \vec{C}\\ \vec{T} &= u \vec{a} + v \vec{b} + w \vec{c} \end{cases}\\ \because \vec{G} \cdot \vec{T} = 2 \pi (hu+kv+lw)\\ \begin{align} \therefore n(\vec{r} + \vec{T}) &= \sum_\vec{G} n_\vec{G} \mathrm{e}^{i\vec{G} \cdot \vec{r}} \mathrm{e}^{i\vec{G} \cdot \vec{T}}\\ &= \sum_\vec{G} n_\vec{G} \mathrm{e}^{i\vec{G} \cdot \vec{r}} \end{align}\]

显然是满足的。

布里渊区 Brillouin zone

布里渊区

布里渊区定义为倒易点阵中的维格纳-赛茨晶胞¹

布里渊区的边界$\vec{k}$ 在中垂线上，故满足：$2\vec{k} \cdot \vec{G} = G^2$. 在实验中，这个 $\vec{k}$ 就是 X 射线入射波的波矢量，衍射点就是边界，通过旋转 X 射线可以得到布里渊区，得到布里渊区就能得到倒易点阵，进一步计算就得到晶体结构。

布里渊区有如下特点：

1. 布里渊区分为第一布里渊区，第二布里渊区，……下图中每种颜色标记一个布里渊区；
2. 每个布里渊区的体积都是相同的，都等于倒易点阵的初基晶胞的体积；
3. 每个布里渊区只包含一个倒阵点阵点

我们一般只考虑第一布里渊区。

布里渊区实例

简单立方：

\[\vec{A}=2\pi \frac{\vec{b}\times \vec{c}}{\Omega}=\frac{2\pi}{a}\hat{x}\\ \vec{B} = \frac{2\pi}{a} \hat{y}\\ \vec{C} = \frac{2\pi}{a} \hat{z}\]

1. 其倒易点阵仍是简单立方，点阵常数为 $2\pi/a$；
2. 第一布里渊区是以原点为体心，边长 $2\pi/a$ 的立方体

（比较简单，就不放图了）

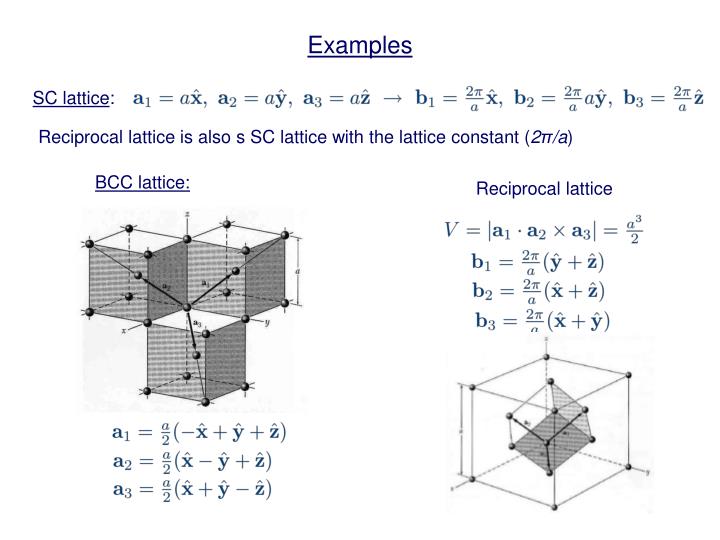
体心立方：

\[\vec{a} = \frac{1}{2}a(\hat{x}+\hat{y}-\hat{z})\\ \vec{b} = \frac{1}{2}a(-\hat{x}+\hat{y}+\hat{z})\\ \vec{c} = \frac{1}{2}a(\hat{x}-\hat{y}+\hat{z})\\ \Omega = \vec{a}\cdot\vec{b}\times\vec{c} = \frac{1}{2}a^3\\ \vec{A} = \frac{2\pi}{a}(\hat{x}+\hat{y})\\ \vec{B} = \frac{2\pi}{a}(\hat{y}+\hat{z})\\ \vec{C} = \frac{2\pi}{a}(\hat{x}+\hat{z})\]

1. 倒易点阵为面心立方
2. 第一布里渊区是正菱形十二面体（周围有 12 个点，有 12 个中垂面）

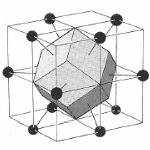
面心立方：

1. 倒易点阵为体心立方（对比下面的式子和上图中的式子）
2. 第一布里渊区是截角八面体（体心立方 8 个顶点 8 个面，面心截去 8 个角）

\[\vec{A} = \frac{2\pi}{a}(\hat{x}+\hat{y}-\hat{z})\\ \vec{B} = \frac{2\pi}{a}(-\hat{x}+\hat{y}+\hat{z})\\ \vec{C} = \frac{2\pi}{a}(\hat{x}-\hat{y}+\hat{z})\]