费米能级
定义与性质
上一节求出的状态密度,仅是能量的密度,但是否有电子,还要看费米分布函数,也就是前面讲自由电子费米气体 时讲过的费米-狄拉克分布:
能量为 $E$ 的一个量子态被一个电子占据的几率为:
\[f(E)=\frac{1}{1+\exp\left( \frac{E-E_f}{kT} \right)}\]式中,$E_f$ 就是费米能级,根据 $\sum_i f(E_i)=N$ 决定。费米分布函数的性质为:
- T=0K 时,$E<E_f, f(E)=1$;$E>E_f, f(E)=0$
- T>0K 时,

费米能级的物理意义
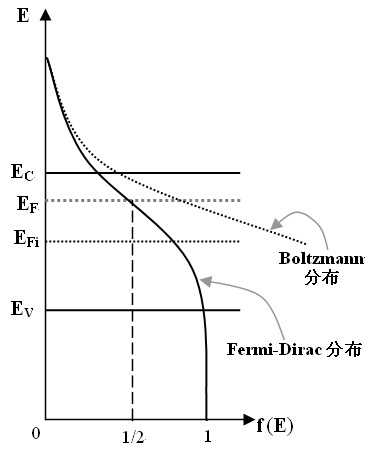
当 $E-E_F>5kT$ 时,$f<0.007$;当 $E-E_F<-5kT$ 时,$f>0.993$,说明电子主要分布在 $E\pm5kT$ 内。所以费米能级标志了电子的填充水平。
当 $E-E_F\gg kT$ 时,$f(E)\approx \exp\left(-\frac{E-E_f}{kT} \right)$$=\exp\left( \frac{E_f}{kT} \right)\exp\left( \frac{-E}{kT} \right)=A\exp\left( \frac{-E}{kT} \right)$,此时费米分布退化为玻尔兹曼分布(只适用于高能情况)
空穴的费米分布
一个地方没电子,那么就是空穴。所以我们有 $f_h(E)+f_e(E)=1$,于是空穴的费米统计分布为:
\[f(E)=\frac{1}{1+\exp\left( \frac{E_f-E}{kT} \right)}\]载流子浓度
电子与空穴浓度
知道了能放几个电子(能态密度$g_c(E)$),知道了电子填充的概率(费米分布函数$f_e(E) uv$),就能得到导带中的电子数:
\[N=\int_{E_c}^{E_c'} g_c(E)f_e(E)\dif E\]从而得到导带中的电子浓度:
\[n=\frac{N}{V}=\frac{1}{V}\int_{E_c}^{E_c'} g_c(E)f_e(E)\dif E\]为了便于计算,我们假设:
- $E-E_F\gg kT$,从而简化为玻尔兹曼分布常数;
- $g_c$ 之前说只能用于极值附近,这里假设 $g_c$ 适用于整个导带。因为在偏离极值的时候,$f_e$ 衰减很快,相乘几乎为0
- 将积分上限改为 $\infty$

最终积分得到:
\[n=\frac{2(2\pi m_{dn}kT)^{3/2}}{h^3} \exp\left(-\frac{E_c-E_f}{kT}\right) = N_c \exp\left(-\frac{E_c-E_f}{kT}\right)\\ N_c=\frac{2(2\pi m_{dn}kT)^{3/2}}{h^3}=4.82\times10^{15} T^{3/2}(\frac{m_{dn}}{m_0})^{3/2}\]同理,我们也可以求到空穴的浓度为:
\[p=\frac{2(2\pi m_{dn}kT)^{3/2}}{h^3} \exp\left(-\frac{E_c-E_f}{kT}\right) = N_v \exp\left(-\frac{E_f-E_v}{kT}\right)\\ N_v=\frac{2(2\pi m_{dn}kT)^{3/2}}{h^3}=4.82\times10^{15} T^{3/2}(\frac{m_{dn}}{m_0})^{3/2}\]对于硅而言,300K,$N_v(\text{Si})=1.1\times10^19 \text{cm}^{-3}$,$N_c(\text{Si})=2.8\times10^19 \text{cm}^{-3}$
学半导体的美妙之处在于,你什么都没干,拍着脑袋就能得到一堆东西。从三维自由空间,得到一个 k空间,得到一个态密度,然后回旋共振得到有效质量,也就是 E 泰勒展开,从有效质量还原出等能面,等能面求导得到能态密度,费米分布又与体系不相干,一积分就得到电子数,再除以晶体体积,就得到电子密度。
载流子浓度乘积
\[n=N_c \exp\left(-\frac{E_c-E_f}{kT}\right) \quad p=N_v \exp\left(-\frac{E_f-E_v}{kT}\right)\\ np=N_c N_v\exp\left(-\frac{E_c-E_v}{kT}\right)=N_c N_v\exp\left(-\frac{E_g}{kT}\right)\]可以看出,载流子浓度乘积只与 $m_e^$,$m_h^$,$E_g$ 和 $T$ 有关,与 $E_F$ 或掺杂浓度无关。因此无论是本征半导体还是杂质半导体,只要是热平衡状态的非简并半导体,都适用。
本征半导体
本征半导体的载流子浓度
T=0K,价带全满,导带全空。T≠0K,热激发,电子从价带激发到导带(本征激发)。因此,T>0K 时,$n=p=n_i$,$n\cdot p=n_i^2$ (本征半导体电中性条件),所以:
\[n_i=\sqrt{np}=\sqrt{N_c N_v\exp\left(-\frac{E_c-E_v}{kT}\right)}=\sqrt{N_c N_v}\exp\left(-\frac{E_c-E_v}{2kT}\right)\\ =4.82\times10^{15} \left( \frac{m_{dn}m_{dp}}{m_0^2} \right)^{3/4} T^{3/2} \exp\left(-\frac{E_g}{2kT}\right)\]对于硅,300K 时,$E_g=1.12eV$,$n_i=1.5\times10^{10} \text{cm}^{-3}$(测量值)
我们对上面的公式进行变形:
\[\ln \left( n_i T^{-3/2}\right)=-\frac{E_g}{2k}\frac{1}{T} + B\]我们可以通过测量得到 $n_i$,而 $T$ 是已知的,所以我们可以得到下图:
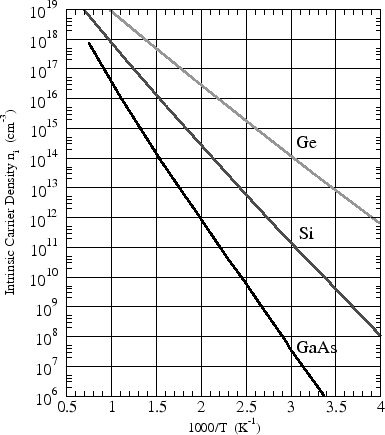
从图中可以看出,斜率 $\frac{E_g}{2k}\propto E_g$,斜率越大,禁带宽越大。
当温度越来越高时,载流子浓度很大,可以看成是导体。我们定义 极限工作温度 为 $n_i<5\times10^{14}\text{cm}^{-3}$ 时的温度。因此,从图中可以看出,GaAs 的极限工作温度比 Si, Ge 都高,所以称为“高温”半导体。
本征半导体的费米能级位置
由 $n=p$,我们有:
\[n=N_c \exp\left(-\frac{E_c-E_f}{kT}\right)=N_v \exp\left(-\frac{E_f-E_v}{kT}\right)=p\\ E_f=\frac{E_c+E_v}{2}+\frac{kT}{2}\ln \left( \frac{N_v}{N_c} \right)\]因为 $\frac{E_c+E_v}{2} \gg \frac{kT}{2}\ln \left( \frac{N_v}{N_c} \right)$,所以我们认为本征费米能级 $E_i$ 基本在禁带中线处。对于硅,300K 时,$E_f=\frac{E_c+E_v}{2}-0.013\text{eV}$
杂质半导体
杂质半导体的载流子浓度
能带中的能级可以容纳 2 个电子,但杂质能级只能容纳 1 个电子。可以证明,电子/空穴占据杂质能级的概率为:
| 电子占据施主能级的几率 | 空穴占据受主能级的几率 |
|---|---|
| $$ f_D(E)=\frac{1}{1+\frac{1}{2}\exp\left( \frac{E_D-E_f}{kT} \right)} $$ | $$ f_A(E)=\frac{1}{1+\frac{1}{4}\exp\left( \frac{E_f-E_A}{kT} \right)} $$ |
对 $f_D(E)$:
- 当 $E_D-E_f\gg kT$ 时,$f_D(E)\rightarrow0$,施主能级远大于费米能级,而费米能级表示填充水平,说明施主能级几乎全电离
- 当 $E_f-E_D\gg kT$ 时,$f_D(E)\rightarrow1$,施主能级远小于费米能级,说明施主能级几乎没电离。
- 一般情况下,$0<f_D(E)<1$,当 $E_D=E_f$ 时,$f_D(E)=2/3$
从而 施主能级上的电子浓度 $n_D=N_Df_D(E)$,受主能级上的空穴浓度 $p_A=N_Af_A(E)$。我们以 n 型半导体中的载流子浓度为例:
假设只有一种施主杂质:$E_D, N_D$,由电中性条件:
\[\begin{align} n_0&=n_D^++p_0\\ 导带电子浓度&=电离施主浓度+价带空穴浓度 \end{align}\]即:
\[N_c\exp\left(-\frac{E_c-E_f}{kT}\right) =\frac{N_D}{1+2\exp\left(-\frac{E_D-E_f}{kT}\right)}+N_v\exp\left(-\frac{E_f-E_v}{kT}\right)\]只要 $T$ 确定了,$E_f$ 也随之确定,$n_0$ 和 $p_0$ 也确定。下面就对不同 $T$ 进行讨论。
低温弱电离区
低温弱电离区:$p_0\approx 0$,$n_0=n_D^+ \ll N_D$,电离的施主远小于掺入的杂质
\[N_C\exp\left(-\frac{E_C-E_f}{kT}\right) =\frac{N_D}{1+2\exp\left(-\frac{E_D-E_f}{kT}\right)}\approx \frac{N_D}{2} \exp\left(\frac{E_D-E_f}{kT}\right)\\ \therefore E_f=\frac{E_C+E_D}{2}+\frac{kT}{2}\ln\left( \frac{N_D}{2N_C} \right)\\\]当温度 $T$ 上升时,$N_C$ 也增大(热激发),$N_D$ 不变,所以 $\frac{kT}{2}\ln\left( \frac{N_D}{2N_C} \right)$ 先增加后减小,从而得到下图:
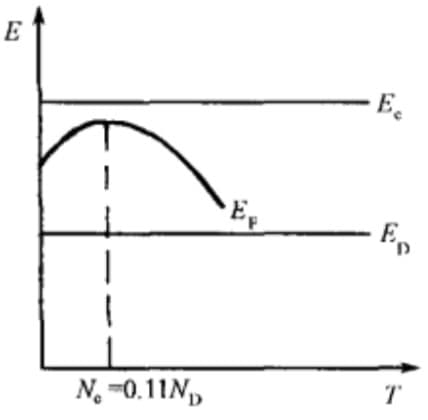
电子浓度为:
\[n_0=\sqrt{n_0 n_D^+}=\sqrt{\frac{N_DN_C}{2}}\exp\left(-\frac{E_c-E_D}{2kT}\right)\\ =\sqrt{\frac{N_DN_C}{2}}\exp\left(-\frac{\Delta E_D}{2kT}\right)\]中等电离区
中等电离区:$p_0\approx 0$,$n_0=n_D^+$
\[N_C\exp\left(-\frac{E_C-E_f}{kT}\right) =\frac{N_D}{1+2\exp\left(-\frac{E_D-E_f}{kT}\right)}\]为了方便求解,我们将左边部分拆开:
\[\begin{align} N_C\exp\left(-\frac{E_C-E_f}{kT}\right)&=N_C\exp\left(-\frac{E_C-E_D+E_D-E_f}{kT}\right)\\ &=\frac{N_C}{2N_D}\exp\left( -\frac{\Delta E_D}{kT} \right)\cdot 2\exp\left( -\frac{E_D-E_f}{kT} \right)\\ 令为\;&=\chi^2\cdot2\exp\left( -\frac{E_D-E_f}{kT} \right) \end{align}\]从而解出:
\[E_f=E_D+kT\ln\left( \frac{\sqrt{\chi^2+4}-\chi}{4\chi} \right)\\ n_0=N_D\left[ \frac{2\chi}{\sqrt{\chi^2+4}+\chi} \right] \quad p_0=\frac{n_i^2}{n_0}\\ 其中,\chi^2=\frac{N_C}{2N_D}\exp\left( -\frac{\Delta E_D}{kT} \right)\]当 $T\rightarrow0$ 时,$\chi\rightarrow0$,从而退化为低温弱电离的结论:
\[由近似关系:\\ \begin{cases} \frac{\sqrt{\chi^2+4}-\chi}{4\chi}=\frac{\sqrt{1+4/\chi^2}-1}{4}\approx\frac{2/\chi}{4}=\frac{1}{2\chi}\\ \frac{2\chi}{\sqrt{\chi^2+4}+\chi}=\frac{2}{\sqrt{1+4/\chi^2}+1}\approx\chi \end{cases} \\ 从而,\\ \begin{cases} E_f=\frac{E_C+E_D}{2}+\frac{kT}{2}\ln\left( \frac{N_D}{2N_C} \right)\\ n_0=\sqrt{\frac{N_DN_C}{2}}\exp\left(-\frac{\Delta E_D}{2kT}\right) \end{cases}\]当温度 $T\rightarrow\infty$ 时,$\chi\gg1$,从而变成强电离区:
\[由近似关系:\\ \begin{cases} \frac{\sqrt{\chi^2+4}-\chi}{4\chi}=\frac{\sqrt{1+4/\chi^2}-1}{4}\approx\frac{1+\frac{1}{2}\frac{4}{\chi^2}-1}{4}=\frac{1}{2\chi^2}(泰勒展开)\\ \frac{2\chi}{\sqrt{\chi^2+4}+\chi}=\frac{2}{\sqrt{1+4/\chi^2}+1}\approx1 \end{cases} \\ 从而,\\ \begin{cases} E_f=E_C+kT\ln\left( \frac{N_D}{N_C} \right)\\ n_0=N_D \end{cases}\]