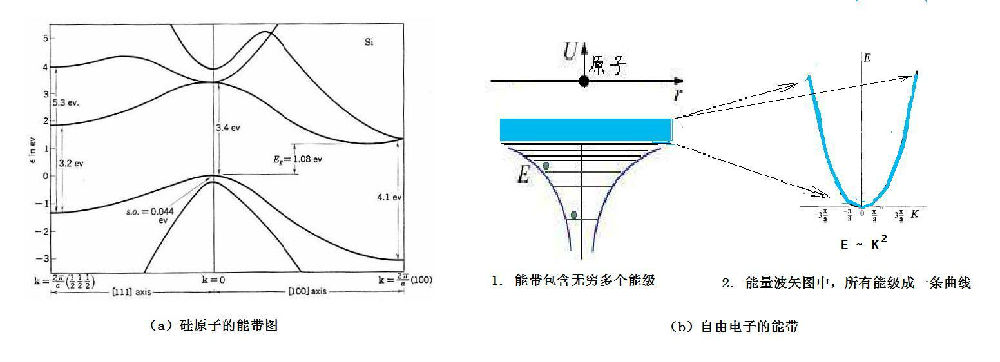
能带与能隙
自由电子模型可以解释金属的热容、热导率、电导率等,但要解释半导体和绝缘体,就要将自由电子模型加以扩充,考虑固体周期性点阵(离子实)的势能作用,最终引入能隙(禁带)。
布拉格定律
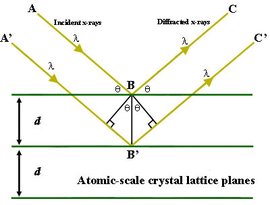
在大学物理光学部分,我们学过,对于满足 $2d\sin\theta = n\lambda$ 的光波,会发生相长干涉,出现强反射。那么对于电子波,是否也会发生这样的反射呢?
近自由电子模型(定性分析)

考虑一维点阵,点阵常数为 $a$,我们考虑上周期性势场,即考虑电子波在离子实的周期性势场中可能发生的布拉格衍射。我们设电子束的波矢为 $\vec{k}$。由前两节,我们知道布里渊区的边界为:$2\vec{k} \cdot \vec{G} = G^2$,正好满足布拉格衍射,所以布拉格衍射条件是:$(\vec{k} + \vec{G})^2 = k^2$,在一维中化简为:
\[k = \pm \frac{n\pi}{a}, \;\text{(n 为正整数)}\]当波矢为 $\pm \pi/a$ 时,波函数不再是行波,而是驻波(反复发生布拉格反射),由向左和向右的两个行波叠加:
\[\psi(+) = e^{i \frac{\pi}{a}x} + e^{-i\frac{\pi}{a}x} = 2 \cos (\frac{\pi}{a}x)\\ \psi(-) = e^{i \frac{\pi}{a}x} - e^{-i\frac{\pi}{a}x} = 2 \sin (\frac{\pi}{a}x)\]两个驻波使电子聚集在不同的空间区域内,考虑离子实的排列,则两个波将具有不同的势能值。
波的几率密度为 $\rho = \lvert\psi\rvert^2$,对于纯粹行波,其几率密度为 1;对于驻波,其几率密度为:
\[\rho(+) = |\psi(+)|^2 \propto \cos^2(\pi x/a)\\ \rho(-) = |\psi(-)|^2 \propto \sin^2(\pi x/a)\]第一条式说明:一部分负电荷聚积在x=0, a, 2a, 的正离子上;第二条式说明:一部分负电荷聚积在相邻离子实的连线中点上。如下图:
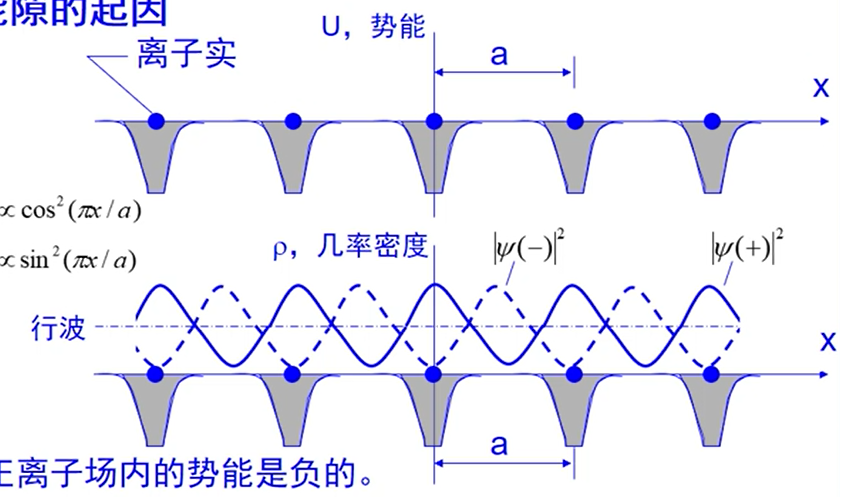
离原子核近的电子的势能更小(绝对值更大),从而三种电荷分布的势能关系为(带负号):$U(+)<U(\text{行波})<U(-)$,$U(+)$ 与 $U(-)$ 能量差即能隙。
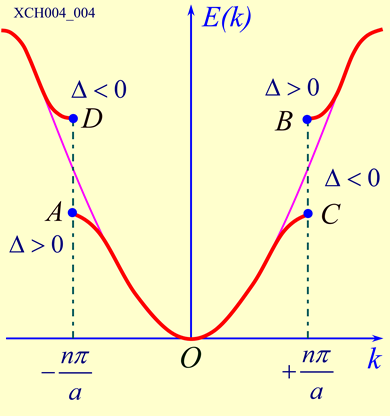 |
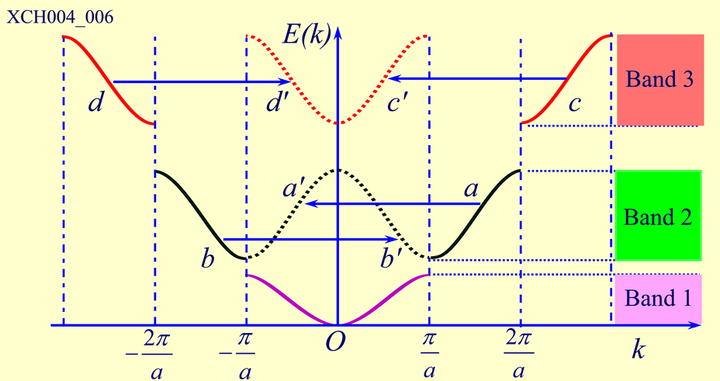 |
上图清楚地表示出能量的差异:
- 自由电子模型对应粉线,$\varepsilon_k = \frac{\hbar}{2m}k^2$,是连续的;
- $\psi(+)$ 对应于 AC,即第一允许能带;
- $\psi(-)$ 对应于 DB,即第二允许能带;
- AB之间、CD之间的部分就是能隙(禁带);
布洛赫函数
布洛赫电子论作了3 条基本假设,即
- 绝热近似,认为离子实固定在其瞬时位置 上,可把电子的运动与离子实的运动分开来处理;
- 单电子近似,认为一个电子在离子实和 其它电子所形成的势场中运动;
- 周期场近似, 假设所有电子及离子实产生的场都具有晶格 周期性。布洛赫电子论相比于金属自由电子论,考虑了电子和离子实之间的相互作用,也考虑了电子与电子的相互作用。
由上我们可以得到布洛赫定理:
- 布洛赫定理
- 对于考虑周期性势场的薛定谔方程,其解必定具有如下的特殊形式:
- $\psi_\vec{k}(\vec{r}) = u_\vec{k}(\vec{r}) e^{i\vec{k}\cdot \vec{r}}$
- 上式称为布洛赫函数。其中,$u_\vec{k}(\vec{r})$ 具有晶体点阵的周期,即 $u_\vec{k}(\vec{r}) = u_\vec{k}(\vec{r} + \vec{T})$,并且依赖于波矢 $\vec{k}$
- 布洛赫函数是一个调幅函数,$u_\vec{k}(\vec{r})$ 决定其幅度,$e^{i\vec{k}\cdot \vec{r}}$ 决定其周期。
克朗尼格-朋奈模型(定量分析)
我们规定一维周期性方阱势场,$U(x)$ 是势能(将电势倒过来,令为正),满足:
\[U(x) = \begin{cases} 0 ,\; (0<x<a)\\ U_0 ,\; (a<x<a+b) \end{cases}\]
我们列出薛定谔方程:$- \frac{\hbar}{2m_e} \frac{\dif^2\psi}{\dif x^2} + U(x) \psi = \varepsilon \psi$,得到通解:
\[\psi = \begin{cases} A e^{iKx} + B e^{-iKx} ,\; (0<x<a)\\ C e^{Qx} + De^{-Qx} ,\; (0<x<a+b) \end{cases}\]约束条件为(有限、连续、单值):
- $\psi$ 和 $\dif \psi/\dif x$ 在 0 和 a 处连续;
- $\psi$ 和 $\dif \psi/\dif x$ 在 a 处的值等于 -b 处的值,但超前一个相位因子 $\exp [ik(a+b)]$(布洛赫定理)。
为了简化结果,我们合理取 $b=0, U_0 = \infty$,则 A、B、C、D 若有解,必满足:
\[(P/Ka) \sin Ka + \cos Ka = \cos ka\]注意,$k$ 才是真实的波矢,$K$ 与能量相关,该式约束了能量和波矢的关系。我们分析这个约束方程,右边显然值在 ±1 之间,所以左边也不能超过 ±1. 作出等号左边式子的图像:
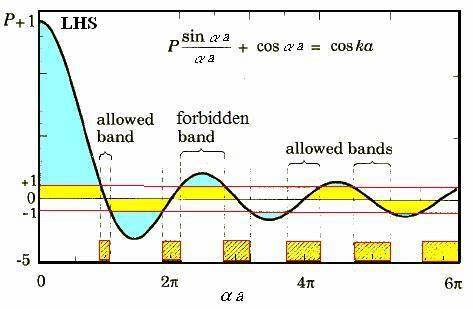
可以发现只有在 allowed band 范围内才有解,也就是导带。上面只是从波的角度进行分析,下面我们从能量角度进行分析:
已知能量的表达式为:
\[\varepsilon = \begin{cases} \frac{\hbar^2 K^2}{2m} ,\; (0<x<a)\\ U_0 - \frac{\hbar^2 Q^2}{2m} ,\; (a<x<a+b) \end{cases}\]在上图中第一个导带内,当 $ka$ 从 0 到 π,$\cos ka$ 从 1 减小到 -1,使得 $Ka$ 右移增加;当 $ka$ 从 π 到 2π,$\cos ka$ 从 -1 增加到 1,使得 $Ka$ 左移减小。随着 $Ka$ 不断在曲线上来回运动,形成了下图中能量最低的那条。
在第二条导带内,能量也会来回变化,但总体上比第一条的高。同理,后面的导带都会产生周期性的能量值,最终形成下面的图像:

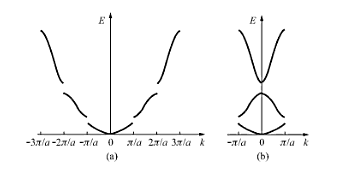
我们可以将所有的 $E-K$ 曲线都平移到第一布里渊区,即简约布里渊区(上图b)。同一 $K$ 值,对应多个 $E$,因此在阐述 $E-K$ 关系时要指明适用的具体能带分支。
对于没有 $K$ 存在的地方,称为禁带,或能隙。有 $K$ 存在的地方为导带或价带。(对导带、价带、能带有点困惑)
能带中的轨道数目
以一维为例,线长 $L=Na$ 的晶体,其波矢为 $k=0,\pm\frac{2\pi}{L},\pm\frac{4\pi}{L},\cdots$,即每间隔 $\frac{2\pi}{L}$ 存在一个允许的波矢,所以第一布里渊区中,有 $N = \frac{2\pi}{a}/\frac{2\pi}{L}$ 个允许的波矢。而每个波矢对应一个轨道,每个轨道可以有两个自旋相反的电子,所以:每个能带中存在 2N 个独立轨道,N为晶体中的初基晶胞数。
三维同理。
如果每个原子贡献两个价电子,则恰好可以填满能带。
半导体晶体
金属是导带半满;绝缘体是导带全空;半导体(半金属)则是除了一个或两个能带是几乎空或几乎满之外,其余所有能带全部填满。
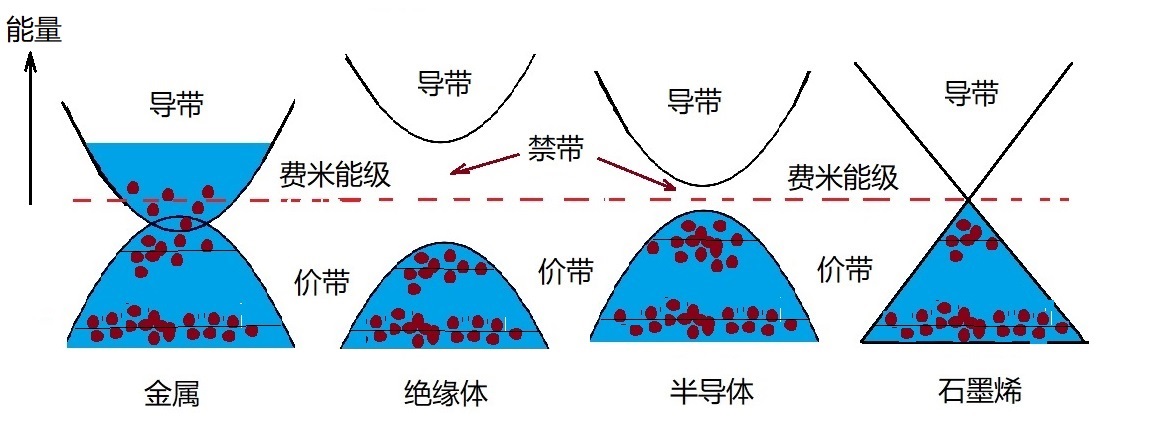
高纯度半导体在绝对零度时,导带为空,与价带相隔一个 $E_g$ 的能带隙(g代表gap),$E_g=导带底-价带顶$. 当温度升高时,电子热激发到导带,导带中的电子和价带中的空轨道都对电导率有贡献。
半导体可以进一步分为两种:
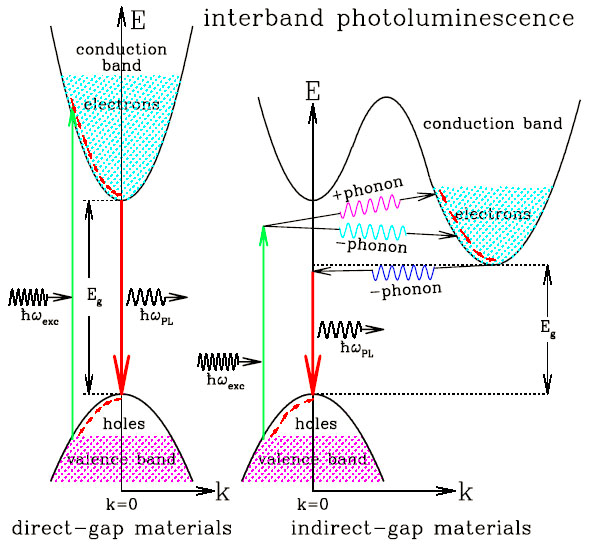
- 直接能隙晶体:导带底和价带顶的 K 相同,当电子吸光跃迁时,不需要动量,非常容易吸收或发出光子。比如:GaAs,常用来作激光。
- 间接能隙晶体:导带底和价带顶的 K 不相同,跃迁除了需要光子,还需要声子(晶格的振动),以满足动量守恒。比如 Si,但仍能用作太阳能。
硅的能带