\[\newcommand{\dif}{\mathop{}\!\mathrm{d}}\]

自由电子模型

自由电子模型认为：组成晶体的原子中束缚得最弱的电子在金属内自由运动。原子的价电子称为传导电子。在自由电子近似中略去传导电子和离子和离子实之间的力（无库伦力）；在进行所有计算时，仿佛传导电子在样品中可以各处自由运动。总能量全部是动能，势能被略去。

自由电子费米气体是指：自由的、无相互作用的、遵从泡利不相容原理¹的电子气

一维情况下的能级和轨道密度（一维无限深势阱）

下面我们利用量子理论和泡利原理，研究一维情况下的自由电子气。

我们假设：

• 质量为 m 的电子被无限高势垒限制在长度为 L 的直线上
• 引入薛定谔方程： $\hat{H} \psi = \varepsilon \psi$
• 电子的波函数 $\psi_n(x)$ 是方程的解
• $\hat{H} = \frac{p^2}{2m}=-\frac{\hbar^2}{2m} \frac{\dif^2}{\dif x^2}$
• 略去 $\hat{H}$ 中的势能
• $p$ 是动量算子 $p = - i \hbar \frac{\dif}{\dif x}$

我们可以列出以下方程：

\[\begin{cases} \begin{align} -\dfrac{\hbar^2}{2m}\dfrac{\dif^2 \psi_n}{\dif x^2} &= \varepsilon_n \psi_n(x)\\ \psi_n(0) &= 0 \text{（边界条件）}\\ \psi_n(L) &= 0 \text{（边界条件）} \end{align} \end{cases}\]

易解得（就是个二阶偏微分而已）：

\[\psi_n(x) = A \sin \big( \frac{2\pi}{\lambda_n}x \big)\\ L = \frac{1}{2}n\lambda_n\]

我们代入回薛定谔方程，可以解出电子能量 $\varepsilon_n = \dfrac{\hbar^2}{2m}\big( \dfrac{n\pi}{L} \big)^2$，$n$ 只能取 $1,2,\cdots$，这说明电子的能量分布是离散的。

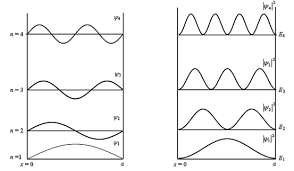
根据泡利不相容原理，两个电子的量子数不能全同，每个轨道最多只能被一个电子占据。我们要把 $N$ 个电子放在这条长 L 的直线上，会有：

• 以同一量子数 $n$ 标记的一对轨道能容纳两个电子，它们自旋相反，能量相同
• 相同能量的轨道可以不止一个，具有相同能量的轨道数目称为 简并度
• 电子先从低能级轨道开始填充

那么，最高填充轨道的能级量子数 $n_F$，为：$n_F = N/2$ （N取偶数）.我们将这个与电子能量$\varepsilon$ 结合在一起，有：

\[\varepsilon_F = \frac{\hbar^2}{2m} (\frac{N\pi}{2L})^2\]

$\varepsilon_F$ 定义为费米能，是基态下最高被充满能级的能量，对应能级为费米能级。我们注意到 $\frac{N}{L}$ 的量纲为长度的倒数，有点像倒易点阵中的矢量，同时其物理意义是“密度”，意味着费米能级不随物体大小而改变。

温度对费米-狄拉克分布的影响

当系统处于绝对零度时的状态称为基态，上面讨论的都是基态情况。当温度升高后，电子气的动能增加，导致某些空的高能级被占据。费米-狄拉克分布函数（Fermi-Dirac distribution） 给出了理想电子气在热平衡时能量为 $\varepsilon$ 的轨道被电子占据的几率：

\[f(\varepsilon) = \dfrac{1}{e^{\frac{\varepsilon - \mu}{kT}}+1}\]

其中，$\mu = \mu(T)$ 是化学式，并且 $\mu$ 的取值要使 $\sum f(\varepsilon_k) = N$

你可以试一试将这个函数进行积分，你会发现这个函数极难积分，原因是分母上有 1，如果能把 1 拿掉，这就是个简单的 $e$ 指数函数。而非常巧的是，半导体体系就可以把 1 拿掉。

在 T = 0K 时，有：

\[\begin{cases} \varepsilon-\mu\rightarrow0^+, f(\varepsilon)\rightarrow0\\ \varepsilon-\mu\rightarrow0^-, f(\varepsilon)\rightarrow1 \end{cases}\]

这说明 在 T = 0K 时，$\varepsilon=\mu$ 以上占据几率为 0，以下占据几率为 1，说明最高能级（即费米能级） $\varepsilon_F=\mu$；而在其他一切温度下，当 $\varepsilon = \mu$ 时，$f(\varepsilon) = \frac{1}{2}$

当 $\varepsilon - \mu \gg kT$ 时，F-D分布简化为 玻尔兹曼分布 $f(\varepsilon) \cong e^{-\frac{\varepsilon - \mu}{kT}}$

三维情况下的自由电子气

三维情况下自由粒子遵循薛定谔方程：

\[-\frac{\hbar}{2m} (\frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2}) \psi_\vec{k}(\vec{r}) = \varepsilon_\vec{r} \psi_\vec{r} (\vec{r})\]

我们考虑在边长 L 立方体中的电子状态，可解得波函数为：

\[\psi_\vec{r} (\vec{r}) = \exp ( i \vec{k}\cdot \vec{r})\]

其中，$\vec{k}$ 是波矢，其的取值为 $k_x, k_y, k_z = 0; \pm \frac{2\pi}{L}; \pm \frac{4\pi}{L};\dots ;\frac{2n\pi}{L}$（与一维类似），从而满足周期为 L：

\[\exp[ik_x(x+L)] = \exp [i \frac{2n\pi}{L}(x+L)] = \exp[ik_x x]\]

由于 $\vec{k}$ 有三个分量，这三个分量确定一个轨道。再加上自旋方向量子数 $m_s$，一共有 4 个量子数。

与一维一样，我们将波函数代回薛定谔方程，可以得到 $\varepsilon-k$ 关系（又称色散关系）：

\[\varepsilon_\vec{k} = \frac{\hbar^2}{2m} k^2 = \frac{\hbar^2}{2m} ( k_x^2 + x_y^2 + x_z^2)\]

轨道 $k$ 中粒子的群速度为 $\vec{v} = \hbar \vec{k} / m$（后面会讲），动量为 $\hbar \vec{k}$（德布罗意波），$k = \frac{2\pi}{\lambda}$，所以我们可以很清楚地看出上面的式子就是动能。

我们把 $k_x, k_y, k_z$ 放到三维空间中（该空间称为 k空间或动量空间），则每个轨道可以表示为一个在球内的点，球面的能量为费米能，费米面上波矢的大小是 $k_F$. 而由于波矢分量是量子化的，所以在 k 空间中，每个体积为 $(2\pi/L)^3$ 的正方体中，只存在一个波矢（电子态），由 $k_x, k_y, k_z$ 决定。每个波矢对应自旋方向相反的两个电子。

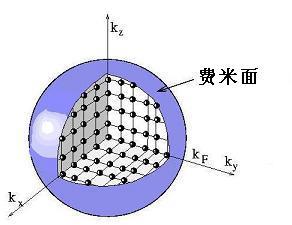
那么，在费米球内，存在的电子总数是： \(2\times (\frac{4}{3} \pi k_F^3 \div (\frac{2\pi}{L})^3) = \frac{V}{3\pi^2} k_F^3 = N\)

从而，解出费米能级：

\[k_F = (\frac{3\pi^2 N}{V})^\frac{1}{3}\\ \Longrightarrow \varepsilon_F = \frac{\hbar^2}{2m} (\frac{3\pi^2N}{V})^\frac{2}{3}\]

说明费米能与体电子浓度 $N/V$ 有关

对于能量小于费米能的轨道，我们有：

\[N = \frac{V}{3\pi^2}(\frac{2m\varepsilon}{\hbar^2})^\frac{3}{2}\]

我们同时对两边微分，可以得到：

\[D(\varepsilon) = \frac{\dif N}{\dif \varepsilon} = \frac{V}{3\pi^2} \cdot (\frac{2m}{\hbar^2})^{\frac{3}{2}} \cdot \varepsilon^{\frac{1}{2}}\]

我们称 $D(\varepsilon)$ 为 能态密度（density of state），指单位能量间隔内的电子数目。三维下的能态密度是一个指数函数（如下图蓝线）

我们一开始只假设了薛定谔方程和周期性，能推出这么多东西，也是蛮厉害的哦？！