\[\newcommand{\dif}{\mathop{}\!\mathrm{d}} \newcommand{\p}{\partial}\]

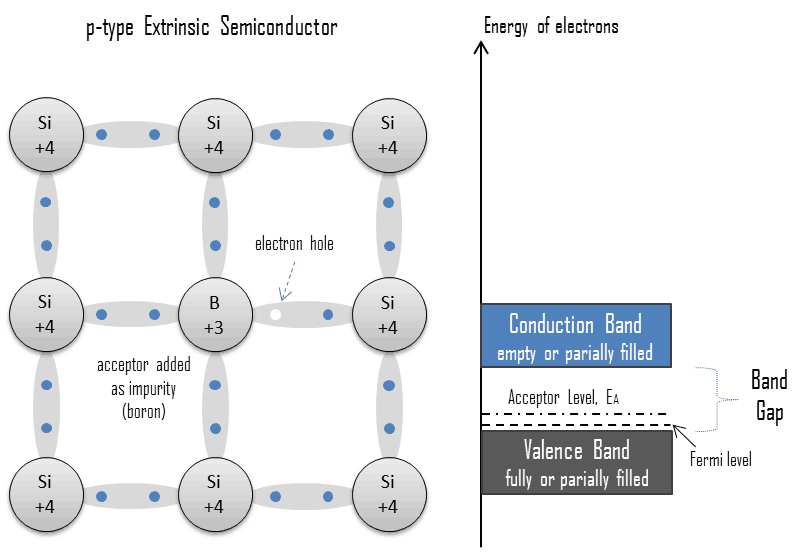
替位式杂质和间隙式杂质

按照球形原子堆积模型，金刚石中的空间利用率只有 34%，所以杂质可能有两种：

杂质浓度：单位体积中的杂质原子数

施主杂质与施主能级

如果参入 Ⅴ族元素P 在 Si 中成为替位式杂质且电离时，能够释放电子且成为正电中心，称为施主杂质（donor）或 n型杂质。施主杂质束缚的电子的能量状态记为$E_D$

下面我们考虑多余的那个价电子的状态和能量。该电子与价带和导带电子不同：

于是我们有以下能带图：

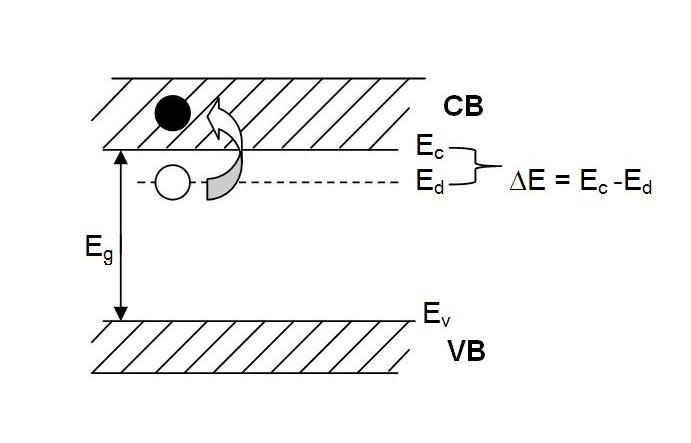
注意几点：

杂质比较少，它的能级是孤立的，未能形成能带，称为孤立能级，用短线表示
$\Delta E_D « E_g$
1. 当 T=0K，束缚态
2. T≠0K，能带角度：电子从 $E_D$ 跃迁到 $E_C$；空间角度：电子脱离 $P^+$ 离子库仑力束缚，成为自由电子。此时的施主杂质处于 离化态

如果参入 Ⅲ 族元素B 在 Si 中成为替位式杂质且电离时，能够接受电子且成为负电中心，称为受主杂质（acceptor）或 p型杂质。空穴的能量状态称为 $E_A$

多余的空穴束缚在负电中心，但这种作用比共价键弱，只要很小能量就能使空穴挣脱束缚，成为自由空穴在晶体种运动。

我们可以用类氢原子模型的计算。

已知氢原子：$E_n=-\frac{m_0e^4}{8\varepsilon_0^2h^2n^2}=-\frac{13.6}{n^2}$（单位：eV）

对硅情况进行修正：

$\varepsilon_0\rightarrow \varepsilon_0\varepsilon_r$，对于硅：$\varepsilon_r(Si)=12$，对于锗：$\varepsilon_r(Ge)=16$
$m_0\rightarrow m^*$，作各向同性处理后：$\frac{1}{m^*}=\frac{1}{3}(\frac{1}{m_l}+\frac{2}{m_l})$

得到类氢模型：

\[E_n=\frac{(m^*/m_0)}{\varepsilon_r^2}\frac{13.6}{n^2}\]

代入后可以算出电离能 $\Delta E_{D(A)}$~几十meV

同时也可以算出 P原子半径：$a^*=24.5$（单位：A），相比之下，硅晶格常数为 5.43（A），可以看出电子几乎

当同时存在施主、受主时，会有杂质补偿作用。

空间角度：施主周围多余的价电子提供给受主，补偿受主的价键，使价键饱和，达到稳定状态
能带角度：定义
1. 有效施主浓度（有效参杂浓度）：$N_{D(eff)}=N_D-N_A$
2. 杂质补偿度：$\gamma=1-\lvert \frac{N_D-N_A}{N_D+N_A} \rvert$，当刚好$N_D=N_A$时，$\gamma=1$，此时载流子浓度很低，几乎和本征半导体一样。

当杂质不是Ⅲ、Ⅴ族杂质时，会引入深能级。特点：

深能级杂质的作用：

以 GaAs 为例，掺入不同元素：