固体物理主要研究晶体和晶体中的电子。 ——C. Kittel
半导体的基本特性:
- 温度效应——负温度系数
- 掺杂效应——杂质敏感性
- 光电效应——光电导
- 电场、磁场效应
半导体特性的原因:晶体结构——》能带结构——》物质性质
晶体
物质可以按照以下分类:
- 气体
- 液体
- 固体
- 非晶体
- 晶体
- 单晶体
- 多晶体
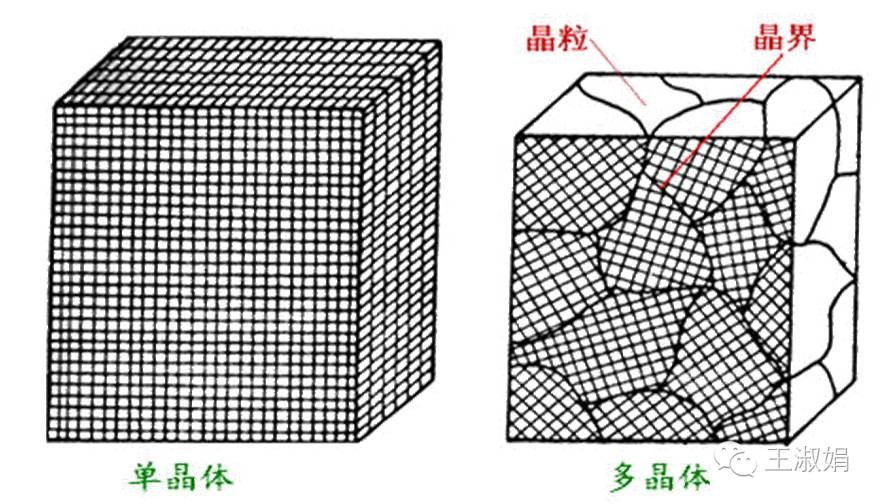
晶体的基本特点:
- 原子按一定方式有规律的排列而成
- 固定的熔点:硅 1420℃,锗 941℃
- 单晶具有方向性:各向异性
- 解理性:晶体在外力作用下沿特定的结晶方向裂开成较光滑断面
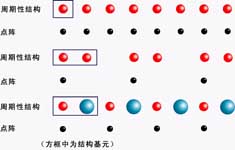
要描述晶体,主要描述原子的周期性阵列。理想的晶体是由全同1 的结构单元在空间无限重复而构成的。这里全同的结构单元可以是单原子、多原子或分子,我们统一用点描述,这种点称为 基元。基元在空间重复形成晶体结构。
点阵平移矢量和点阵
给定三个基本平移矢量a, b, c,以及任意整数 u, v, w:
\[\vec{r}' = \vec{r} + u \vec{a} + v \vec{b} + w \vec{c}\]上式说明,从任意一点 r 去观察原子排列,同从 r’ 点去观察锁看到的原子排列在各方面都是一样的。故引入点阵定义:
- 点阵
- 让 $u, v, w$ 取所有整数,则上述方程所确定的一族点 $r’$ 就定义了一个点阵。点阵+基元=晶体结构
- 初基平移矢量
- 若有任意两个点 $r$ 和 $r’$,通过适当选取整数 $u, v, w$,它们始终满足点阵定义方程,而且所观察到的原子排列是一样的,那么平移矢量 $\vec{a}, \vec{b}, \vec{c}$ 称为初基的。这个定义确保初基平移矢量确定最小的晶胞。
- 通俗来讲,要判断初基平移矢量,一是看能否平移出所有点,二是看面积是否最小
- 我们一般用初基平移矢量定义晶轴,但若非初基平移矢量晶轴更简单,则采用非初基平移矢量

- 点阵平移操作
- 晶体通过晶体平移矢量 $\vec{T} = u \vec{a} + v \vec{b} + w \vec{c}$ 平行于自生的位移。任意两个晶体均可以这种矢量形式连接起来
- 初基晶胞、单胞、原胞
- 初基轴 a, b, c 确定的平行六面体称为一个初基晶胞。初基晶胞是体积最小的晶胞,通过适量平移操作,可以填充整个空间
- 同一点阵,可以有多种方式组成初基轴和初基晶胞,但初基晶胞中的原子数目(密度)都是一样的
选取初基晶胞的方法
方法一:先选取初基轴,再构成初基晶胞。
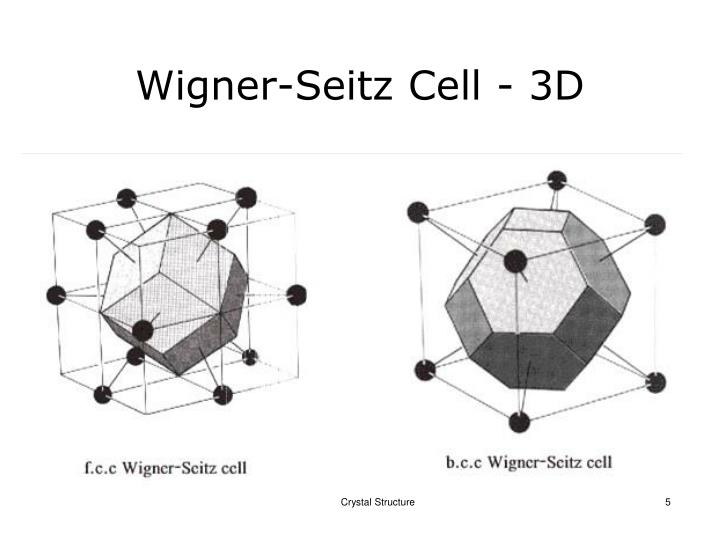
方法二:Wigner-Seitz primitive cell(维格纳-赛茨初基晶胞)
- 把某个阵点与所有相邻的阵点用直线连接起来
- 在连线中点处作垂线或垂面
- 垂线或垂面围成的最小体积就是维-赛初基晶胞

点阵的基本类型:
- 点对称群产生 14 种不同点阵
- 1种一般,13种特殊
- 图中为惯用晶胞,不一定是初基晶胞(比如面心立方)
- 统称 布拉维格子(Bravais lattice)

晶面指数系统
- 晶列
- 点阵中的所有阵点全部位于一系列相互平行的直线上,这些直线系称为晶列
- 晶向
- 表示晶列的方向
- 晶向指数
- 从某个阵点 O 延某个晶列到另一个阵点 P 作位移矢量 $\vec{R} = l_1 \vec{a} + l_2 \vec{b} + l_3 \vec{c}$,取 $mnp$ 三个互质整数,使$l_1 : l_2 :l_3 = m : n : p$,则 [mnp] 称为晶向指数
- 用文字描述为:晶向矢量在三晶轴上投影的互质指数,注意晶轴不一定使初基轴
- 同类晶向记为 <mnp>,如 $<100> = { [100],[\bar{1}00],[010],[0\bar{1}0],[001],[00\bar{1}] }$ (带上横线的为负)
- 晶面指数(hkl)
- h、k、l 是晶面于三晶轴的截距 r、s、t 的倒数的互质整数,也称 密勒指数
- 晶轴不一定使初基轴
- 取倒数是为了避免当截距为0时出现无穷
- 等同晶面用 $\{hkl\}$

常见晶体结构
点阵+基元=晶体结构
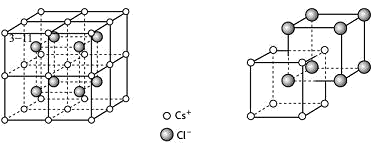
NaCl 结构:面心立方 + NaCl
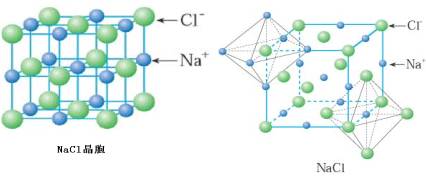
CsCl 结构:简单立方 + CsCl
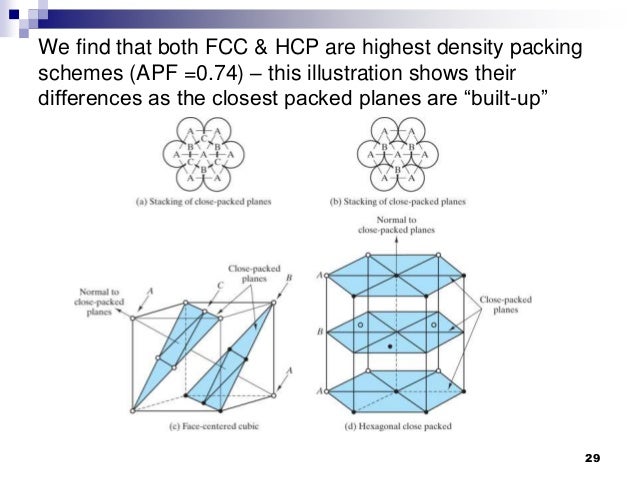
密堆积
- 面心立方 Cubic Closed Packing
- 六角密堆积 Face Centered Cubic

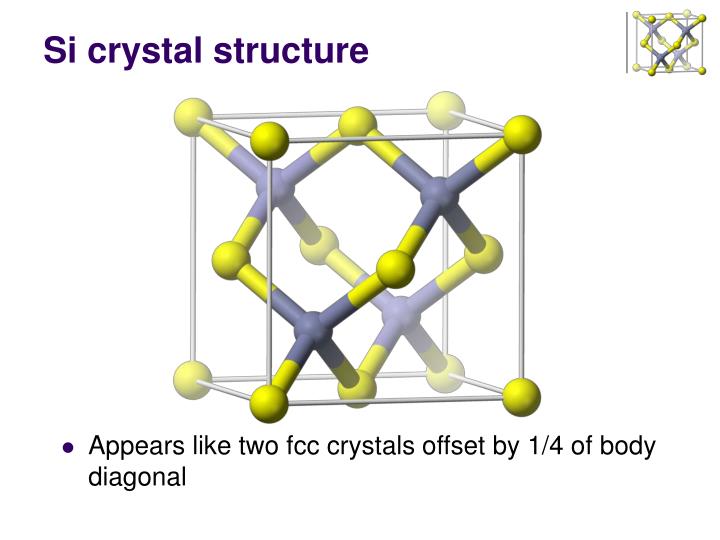
Si晶体 金刚石结构:面心立方+ 2Si原子(这种基元有一个以上原子的点阵称为复式点阵)
-
全同:在空间上、位形上无法区分 ↩