\[\newcommand{\dif}{\mathop{}\!\mathrm{d}} \newcommand{\p}{\partial}\]

回旋共振

不同半导体材料，其能带结构不同，而且往往是各向异性的，不同波矢$k$方向，$E-k$ 关系不同。$E-k$ 关系对研究和理解半导体中的载流子行为很重要，然而理论上尚存在困难，所以要用“回旋共振实验”来测出 $E-k$ 关系。

等能面

$E(k)$ 为一定值时，对应许多不同的 $k=(k_x, k_y, k_z)$，将这些 $k$ 连接起来构成一个封闭面，称为等能面。

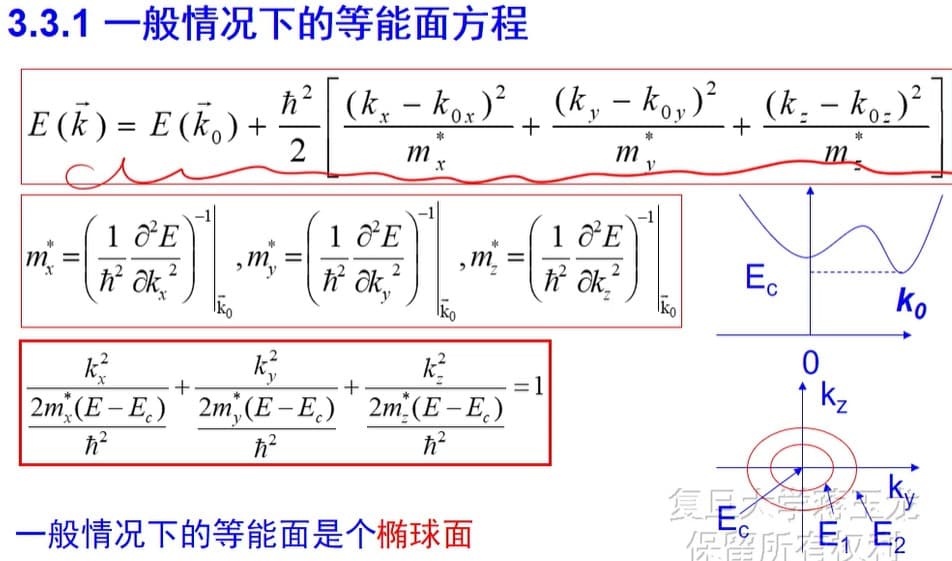
但在空间中，由于晶体的各向异性，不同波矢$k$方向，$E-k$ 关系不同，同时能带极值也不一定在 $k=0$ 处。我们设导带底为 $k_0$，$E(k_0)$，坐标轴为 $k_x, k_y, k_z$，我们定义：$m_x^*, m_y^*, m_z^*$ 为相应方向的导带底电子有效质量。我们在 $k_0$ 极值附近进行三维泰勒展开。

\[E(\vec{k})=E(\vec{k_0})+\frac{\p E}{\p \vec{k}}\Big\vert_{\vec{k}=\vec{k_0}}\cdot(\vec{k}-\vec{k_0})+\frac{\p^2 E}{\p \vec{k}^2}\Big\vert_{\vec{k}=\vec{k_0}}\cdot(\vec{k}-\vec{k_0})^2\]

则我们有：