- 基本概念
- 流网络、网络上的流、最大流;流网络的切、最小切
- 流和切的关系、净流量,弱对偶性: 切流值≤切的容量;最大流与最小切的关系
- 流的数学性质
- 最大流算法
- 残差网络/剩余图(Residual graph)
- Ford-Fulkerson算法:一个贪心方法
- 增广路径
- Edmonds-Karp 算法
- 选取剩余图中边数最少的增广路径的Ford-Fulkerson方法
- 多尺度实现
网络流
给定有向图 $G=(V,E)$,其中,两个特殊的点 s 和 t 被称为 源(Source) 和 汇(Sink),而 $E$ 中的每条边有一个容量值(capacity) $c(u,v)$。则这四个东西组合起来的 $(G,s,t,c)$ 称为流网络。
最大流问题
求从 $s$ 到 $t$ 的最大流量就是最大流问题。最大流问题在交通规划、物流管理、网络流量等都会遇到。
我们考虑如下宴会座位安排问题:有 $N$ 个家庭参加, 每个家庭人数分别是 $𝑎1,𝑎2,\cdots,a_n$,有 $m$ 张餐桌,每张能容纳 $c_1,c_2,\cdots,c_n$ 个人。为了增进友谊,要求每个家庭同桌数不多于 $k$,那么我们可以转化为如下最大流问题:
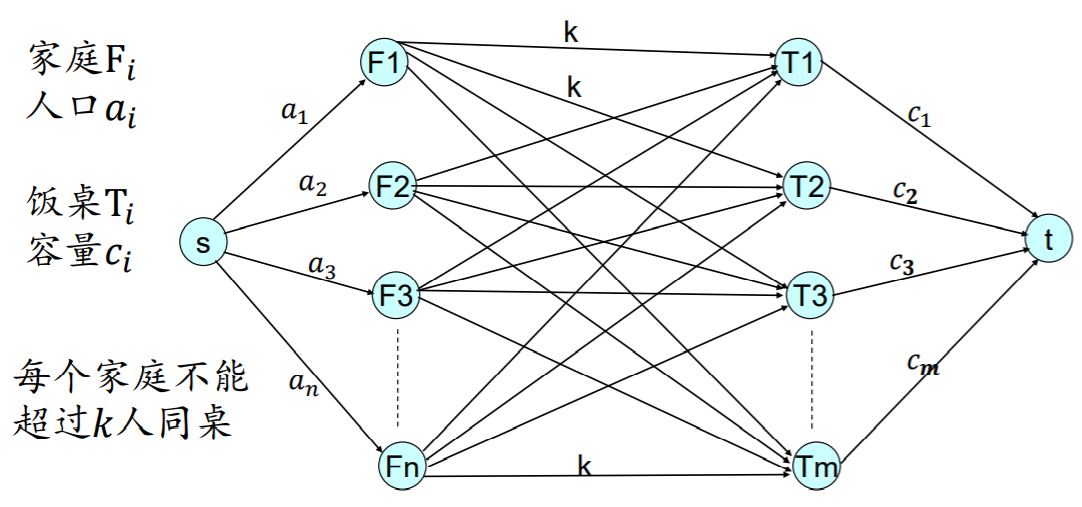
要解决这个问题,可以采用 Ford-Fulkerson 算法,在了解这个算法之前,先弄清楚几个概念:
- 残存网络:给定一个流网络G和一个流,流的残留网Gf拥有与原网相同的顶点。原流网络中每条边将对应残留网中一条或者两条边,对于原流网络中的任意边(u, v),流量为f(u, v),容量为c(u, v):
- 如果f(u, v) > 0,则在残留网中包含一条容量为f(u, v)的边(v, u);
- 如果f(u, v) < c(u, v),则在残留网中包含一条容量为c(u, v) - f(u, v)的边(u, v)。
- 简单来说,就是将边上的容量减去流量,然后再加上一条相反的边,相反的边的容量就等于流量。
Ford-Fulkerson 算法的过程如下:
- 选一条增广路径,让路径上的流达到最大值,记录这个容量
- 做出残存网络
- 重复 1、2 直到无法做出路径
- 最大流量就是所有记录的容量和。
参考:知乎:最大流
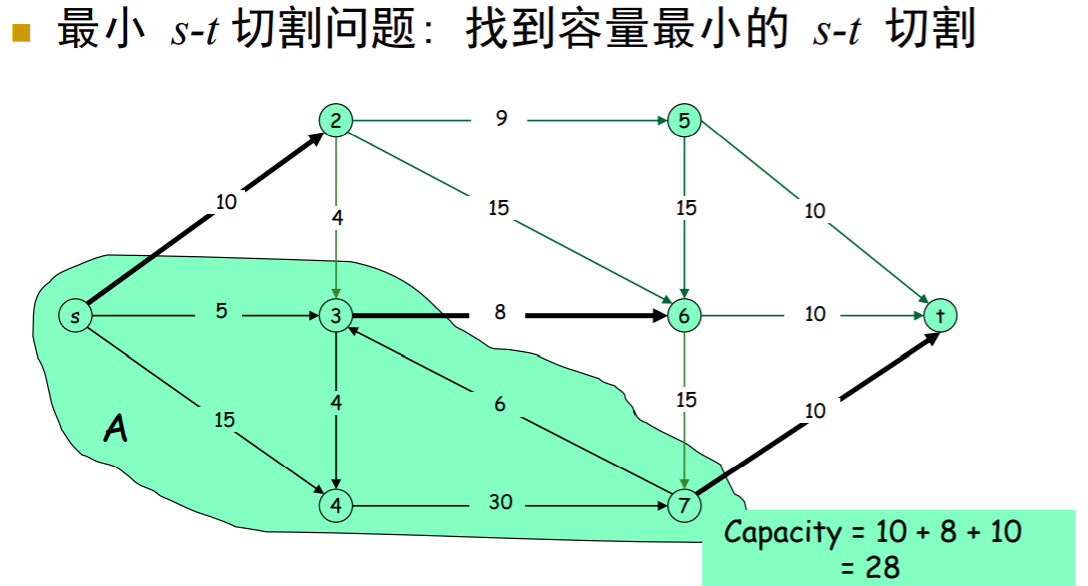
最小切问题
最小切问题指的是:找到容量最小的切割把s和t分开。也就是说,我们需要将结点划分成两部分,两部分之间的流量最小。