- 具体算法
- 矩阵链乘
- 最长公共子串
- 最大字段和
- 凸多边形的最优三角剖分
- 多边形游戏
- 流水作业调度
- 0-1背包
- 动态规划算法的基本要素
- ①最优性原理(最优子结构)②重叠子问题
- 动态规划算法的递归式
- 动态规划算法设计的四个步骤
- 找出最优解的性质,并刻画其结构特征;
- 递归地定义最优值;
- 以自底向上的方式计算最优值(也可以自顶向下);
- 根据计算最优值时得到的信息构造最优解。
- 对上述每个具体算法
- 掌握其相应的动态规划基本要素的具体含义,比如最优子结构,递归式,自底向上计算,伪代码描述、复杂度等 给定输入,能追踪算法的求解过程,
- 算法分析题3-1, 3-3, 3-4;
动态规划
动态规划(dynamic programming) 通过将复杂问题分解为子问题,并且保存子问题的解,从而避免重复计算。动态规划具有下面两个特征:
- 子问题重复(重叠子问题性质)
- 最优性原理(最优子结构性质)
子问题重复
与分治问题一样,动态规划问题的解由子问题组合得到。不同的是,动态规划中,子问题的解可能需要重复用很多次,所以我们一般将子问题的解保存在一维或二维数组中。比如,二分查找显然不需要重复用子问题的解,所以用分治即可;而斐波那契数列则会重复用到子问题的解,用动态规划会比分治更快。
#递归与分治算法
def fib(n):
if n <= 1:
return n
return fib(n-1) + fib(n-2)
fib(5)
/ \
fib(4) fib(3)
/ \ / \
fib(3) fib(2) fib(2) fib(1)
/ \ / \ / \
fib(2) fib(1) fib(1) fib(0) fib(1) fib(0)
/ \
fib(1) fib(0)
我们可以用动态规划来解决斐波那契数列。既然上面要重复计算,那我们不妨将结果保存在一个数组里,当数组里面没有对应数时才递归调用:
def fib(n, lookup): #需要准备一个长度为 n+1 的空数组
if n == 0 or n == 1:
lookup[n] = n
if lookup[n] is None:
lookup[n] = fib(n-1 , lookup) + fib(n-2 , lookup)
return lookup[n]
另一种简单的方法就是从 0 一直算到 n,并保存前面的解:
def fib(n):
f=[0,1]
for i in range(2,n+1)
f.append([i-1] + f[i-2])
return f[n];
这就是动态规划的第一个特点:子问题重复。
最优性原理
最优性原理指的是:如果主问题满足最优解,那么子问题也应该满足最优解。比如,求解 A,B 两点之间最短的路径,如果 C 是路径上的一点,那么 A 和 C、C 和 B 之间的路径也应该是最短。(这道题留给以后写)
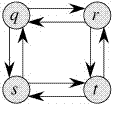
一个相反的例子就是最长简单路径问题,比如下图中,q 到 t 的最长路径有两个:q→r→t 和 q→s→t,但是 q→r 之间的路径并不是最长路径。
解决动态规划问题的步骤
识别动态规划问题
一般来讲,动态规划问题有以下特征:
- 求解最大(最长、最多……)或最小(最短、最少……)值,或者是求解满足某条件的排列的数量
- 所有动态规划问题都会满足子问题重复的特点,并且大多数还会满足最优性原理。
定义“状态”
动态规划问题主要是状态以及状态之间的转化。这里的“状态”主要指的是子问题的参数,比如上面斐波那契数列的状态就是 n。定义状态的过程相当于是分解为子问题的过程,不同的定义方法会得到不同的解法。
得到状态之间的关系式
这一部分是动态规划问题的最难的一步,需要直觉、观察还有大量的练习。下面举一个例子:
我们有 3 种面额的纸币,分别是 1、3、5。假如付款 N 元,问总共有几种组合方法。这里的状态就是 n,每个 state(n) 对应着组合数。那么显然,我们有 state(n) = state(n-1)+state(n-3)+state(n-5),对应的代码如下:
def solve(n):
if n<0:
return 0
if n==0:
return 1
return solve(n-1)+solve(n-3)+solve(n-5)
增加存储部分
这部分就很简单了,只要将状态的解保存起来就行了。状态有 n 个参数,我们就用 n 维数组保存。
dp=[]
def solve(n):
global dp
if len(dp)<n+1:
dp=[-1 for i in range(n+1)]
if n<0:
return 0
if n==0:
return 1
if dp[n]==-1:
dp[n]=solve(n-1)+solve(n-3)+solve(n-5)
return dp[n]
至此,动态规划问题已经全部解决。
矩阵连乘问题
问题描述 求 $n$ 个矩阵连乘的乘积:$A_1A_2 \cdots A_n$
问题分析
矩阵的乘法满足结合律,比如我们考虑如下矩阵相乘:
\[A_{4\times3}A_{3\times2}A_{2\times3}\\ (A_{4\times3}A_{3\times2})A_{2\times3}\rightarrow 4\times 3 \times 2 + 4\times 2 \times 3=48次\\ A_{4\times3}(A_{3\times2}A_{2\times3})\rightarrow3\times 2 \times 3 + 4\times 3 \times 3=54次\]可以看出,不同的结合法需要相乘的次数不同。回到原问题,我们考虑最后一次乘法,即 $(A_1\cdots A_k)(A_{k+1}\cdots A_n)$,在最优的情况下,左右两个子乘积也是最优解。
我们设 $A_i\cdots A_j$ 的最优次数为 $C(i,j)$。最后一次的乘法为 $(A_i \cdots A_k)(A_{k+1} \cdots A_j)$,对应的乘法次数为:$p_i \times q_k \times q_j$($p$ 为行数,$q$ 为列数),那么,我们有:
\[C(i,j)=\min_{i\leq k < j} \{ C(i, k)+C(k+1,j)+ p_i \times q_k \times q_j\}\]我们构造如下矩阵:
\[\boldsymbol{C}_{ij}= \begin{bmatrix} C_{11} & C_{12} & \cdots & C_{1n}\\ & C_{22} & \cdots & C_{2n}\\ & & \ddots & \vdots\\ & & & C_{nn} \end{bmatrix}\]显然,对角线上的元素为 0. 而第 2 条对角线上的 $C_{i,i+1}$ 为 $p_i\times q_i \times q_{i+1}$。从第 3 条对角线开始,$C_{ij}=\min { \cdots }$。然后不断地迭代,最终算出第 n 条对角线上的 $C_{1n}$,也就是问题的结果。
如果我们将每个 $C_{ij}$ 对应的 $k$ 记录下来,那么我们就能得到最少次数乘法的步骤。
Python代码
点击展开
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
def matrixChain(mat): # mat[n][i][j]
# 确定 C 矩阵与 k 矩阵的大小
# k矩阵用于记录分割点
n = len(mat)
if n <= 1:
return 0, [], []
# 确定是否符合矩阵相乘条件
len_mat = [len(mat[0])]
for i in range(1, n):
if len(mat[i-1][0]) != len(mat[i]): #行等于列
return -1, [], []
len_mat.append(len(mat[i]))
len_mat.append(len(mat[-1][0]))
# 初始化 C 矩阵与 k 矩阵
# 第 1 条对角线上为 0
C_matrix = []
k_matrix = []
for i in range(n):
C_matrix.append([0 for j in range(n)])
k_matrix.append([0 for j in range(n)])
# 计算第 2 条对角线
for i in range(n-1):
C_matrix[i][i+1] = len_mat[i]*len_mat[i+1]*len_mat[i+2]
k_matrix[i][i+1] = i
# 计算后面的对角线
for j in range(2, n):
for i in range(0, n-j):
for k in range(i, i+j):
times = C_matrix[i][k]+C_matrix[k+1][i+j] + \
len_mat[i]*len_mat[k+1]*len_mat[i+j+1]
if k == i: # 初始化第一个 C_min
C_min = times
k_min = k
elif times < C_min: # 更新 C_min
C_min = times
k_min = k
C_matrix[i][i+j] = C_min
k_matrix[i][i+j] = k_min
return 1, C_matrix, k_matrix
A = [[1, 1, 1],
[2, 2, 2],
[3, 3, 3],
[4, 4, 4]]
B = [[1, 1],
[2, 2],
[3, 3]]
C = [[1, 1, 1],
[2, 2, 2]]
mat = [A, B, C]
i, C_matrix, k_matrix = matrixChain(mat)
print(C_matrix[0][-1])
最长公共子串
问题描述 在两个字符串 $X$,$Y$ 中,查找最长的公共子串。子串可以不连续,但要保持顺序。(Longest Common Subsequence)
问题分析
设字符串为 $X[0..m-1]$ 和 $Y[0..n-1]$,并设 $L(X[0..m-1],Y[0..m-1])$ 表示 $X,Y$ 的最长公共子串。有如下最优子问题:
- 如果最后一个字母的相同,则 $L(X[0..m-1],Y[0..m-1])$$=1+L(X[0..m-2],Y[0..n-2])$
- 如果最后一个字母不相同,则 $L(X[0..m-1],Y[0..n-1])$$=\max { L(X[0..m-2],Y[0..n-1]),$$L(X[0..m-1],Y[0..n-2])}$
def lcs(X, Y, m, n):
if m == 0 or n == 0:
return 0;
elif X[m-1] == Y[n-1]:
return 1 + lcs(X, Y, m-1, n-1);
else:
return max(lcs(X, Y, m, n-1), lcs(X, Y, m-1, n));
# Driver program to test the above function
X = "AGGTAB"
Y = "GXTXAYB"
print "Length of LCS is ", lcs(X , Y, len(X), len(Y))
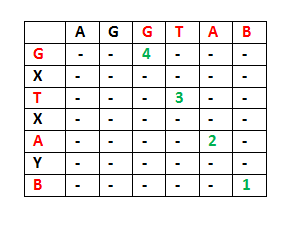
为了避免重复计算,我们构造一个 $m\times n$ 的矩阵,其中第 $i$ 行第 $j$ 列存储 $L(X(0..i),Y(0..j))$。代码如下:
# Dynamic Programming implementation of LCS problem
def lcs(X , Y):
# find the length of the strings
m = len(X)
n = len(Y)
# declaring the array for storing the dp values
L = [[None]*(n+1) for i in range(m+1)]
"""Following steps build L[m+1][n+1] in bottom up fashion
Note: L[i][j] contains length of LCS of X[0..i-1]
and Y[0..j-1]"""
for i in range(m+1):
for j in range(n+1):
if i == 0 or j == 0 :
L[i][j] = 0
elif X[i-1] == Y[j-1]:
L[i][j] = L[i-1][j-1]+1
else:
L[i][j] = max(L[i-1][j] , L[i][j-1])
# L[m][n] contains the length of LCS of X[0..n-1] & Y[0..m-1]
return L[m][n]
#end of function lcs
# Driver program to test the above function
X = "AGGTAB"
Y = "GXTXAYB"
print("Length of LCS is ", lcs(X, Y))
显然,有两个嵌套的循环,复杂度为 $O(mn)$。