回溯算法

回溯算法概述

回溯算法有点像走迷宫，我们要寻找到解的路径，可以先随便选一个方向，如果走不通，那就退回来，换条路走。如果是以树来描述，就是从根出发搜索解空间树，如果某个结点不符合要求，就舍去以该结点为根的子树。一般来讲，主要采用深度优先搜索。

所以回溯的套路也很简单，请看这篇文章：回溯算法套路详解，文中提供了一个框架：

result = []
def backtrack(路径, 选择列表):
    if 满足结束条件:
        result.add(路径)
        return

    for 选择 in 选择列表:
        做选择
        backtrack(路径, 选择列表)
        撤销选择

这个框架会遍历所有解。如果只是需要一个解，可以改成：

result = []
def backtrack(路径, 选择列表):
    if 满足结束条件:
        result.add(路径)
        return True  #改动

    for 选择 in 选择列表:
        做选择
        if backtrack(路径, 选择列表): #改动
            return True #改动
        撤销选择

下面是各种简单例子。

Knight’s Tour Problem 骑士巡游

问题描述

国际象棋中的骑士和中国象棋中的马的走法一样（骑士的标志也是马）。现在问：骑士在 $8×8$ 棋盘中的某一点出发，如何能不重复地走遍每一个格子？

问题分析

我们的目标是给出一个 $8×8$ 的矩阵，矩阵中的数代表骑士走的顺序（如下图）。为了方便起见，假定从左上角出发。每次检查骑士周围可走的格子，如果没走过则将骑士移到该点，然后进行递归，递归如果有解，那程序就结束；如果递归无解，那就撤销这步。

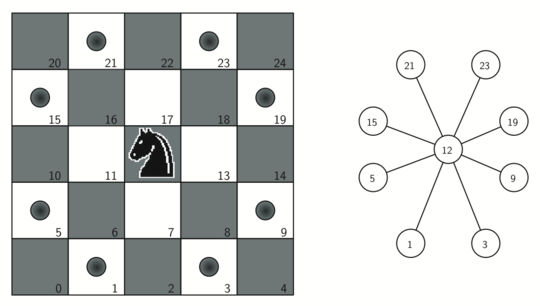
考虑选择列表。根据骑士的走法，假如骑士在 $(i,j)$ 点，那么它下一步可以走：$(i\pm1, j\pm2)$，$(i\pm2,j\pm1)$ 共八个格子。格子必须未走过，并且要求格子要在 $[0,7]$ 范围内，以防过界。所以有如下判断函数：

n = 8
  
def isSafe(x,y,board): 
    ''' 
        判断(x,y)是否可行 
    '''
    if(x >= 0 and y >= 0 and x < n and y < n and board[x][y] == -1): 
        return True
    return False

考虑结束条件。当骑士走了 $8^2$ 步时，说明棋盘已走完。

于是根据上面的框架，我们有：

def solveKT(n,board,curr_x,curr_y,move_x,move_y,pos):
    '''
        n: 棋盘面积
        board: 棋盘的解矩阵
        curr_x,curr_y: 当前位置
        move_x,move_y: 下一步
        pos: 步数
    '''
    if(pos == n**2): #board 已是解
        return True

    for i in range(8):
        #下一步
        new_x = curr_x + move_x[i] 
        new_y = curr_y + move_y[i]
        
        #判断下一步是否有效
        if(isSafe(new_x,new_y,board)):
            #将下一步加入解 
            board[new_x][new_y] = pos 
            if(solveKT(n,board,new_x,new_y,move_x,move_y,pos+1)): 
                return True
            
            #回溯 
            board[new_x][new_y] = -1
    return False

board = [[-1 for i in range(n)]for i in range(n)]
move_x = [2, 1, -1, -2, -2, -1, 1, 2]
move_y = [1, 2, 2, 1, -1, -2, -2, -1]
board[0][0] = 0
pos = 1
if(not solveKT(n, board, 0, 0, move_x, move_y, pos)):
    print("无解")
else:
    for i in range(n): 
        for j in range(n): 
            print(board[i][j],end =' ')

#结果
[[ 0 59 38 33 30 17  8 63]
 [37 34 31 60  9 62 29 16]
 [58  1 36 39 32 27 18  7]
 [35 48 41 26 61 10 15 28]
 [42 57  2 49 40 23  6 19]
 [47 50 45 54 25 20 11 14]
 [56 43 52  3 22 13 24  5]
 [51 46 55 44 53  4 21 12]]

回溯并不是解决骑士问题的最好方法。可以看看Warnsdorff’s algorithm for Knight’s tour problem

练习 Rat in a Maze：给出一个 $N\times N$ 的迷宫矩阵，矩阵中 0 代表墙，1代表路。以 $(0,0)$ 为起点，$(N-1,N-1)$ 为终点，求迷宫的解矩阵。

#迷宫矩阵
{1, 0, 0, 0}
{1, 1, 0, 1}
{0, 1, 0, 0}
{1, 1, 1, 1}
#解矩阵
{1, 0, 0, 0}
{1, 1, 0, 0}
{0, 1, 0, 0}
{0, 1, 1, 1}

N Queen Problem N皇后

问题描述 国际象棋中的皇后可以打横、打竖、打斜走。现在要在 $N\times N$ 上的棋盘上放上 $N$ 个皇后，要求皇后不能吃到其他皇后，问怎么放？

问题分析 pandaun 和上面的骑士问题差不多。每一行都从左到右试，如果可行，就设为 1（表示放上皇后）；如果所有都不可行，就撤销这一步。

由于我们是从上往下放每一行的皇后，所以判断是否可行时，我们只需要看上半部分是否有皇后即可。

def isSafe(board, row, col): 
  
    # 检查上面的列 
    for i in range(col): 
        if board[row][i] == 1: 
            return False
  
    # 检查左上对角线 
    for i, j in zip(range(row, -1, -1),  
                    range(col, -1, -1)): 
        if board[i][j] == 1: 
            return False
  
    # 检查右上对角线 
    for i, j in zip(range(row, N, 1),  
                    range(col, -1, -1)): 
        if board[i][j] == 1: 
            return False
  
    return True

def solveNQ(board, col): 
    '''
    board: 解矩阵
    col: 当前要放的行
    '''

    # 已填满所有行，board 已是解
    if col >= N: 
        return True

    # 从左到右试
    for i in range(N): 
        # 判断是否可放
        if isSafe(board, i, col): 
            #做选择
            board[i][col] = 1

            if solveNQUtil(board, col + 1) == True: 
                return True
            #撤销选择
            board[i][col] = 0
    #当前行没有可放的位置
    return False

board = [ [0, 0, 0, 0], 
          [0, 0, 0, 0], 
          [0, 0, 0, 0], 
          [0, 0, 0, 0] ]
N = 4
if solveNQUtil(board, 0) == False: 
    print ("无解") 
    return False
  
printSolution(board)

m Coloring Problem 图着色问题

问题描述

给定一个无向图以及 $m$ 种颜色，要给每个结点上色，使得相邻结点的颜色不同，求上色方案？

这个问题实际上就是 4色问题的特例。

问题分析

我们用一个列表储存每个结点的颜色。每对一个结点涂色后，检查相邻的结点是否有相同颜色即可。

def isSafe(graph, v, colour, c): 
    for i in range(v+1): 
        if graph[v][i] == 1 and colour[i] == c: 
            return False
    return True

def isSafe(graph, v, colour, c): 
    for i in range(len(graph)): 
        if graph[v][i] == 1 and colour[i] == c: 
            return False
    return True

def graphColour(graph, m, colour, v): 
    '''
    graph: 无向图
    m: m种颜色
    colour: 存储涂色的列表
    v: 当前结点
    '''
    if v == len(graph): 
        return True
  
    for c in range(1, m + 1): 
        if isSafe(graph, v, colour, c) == True: 
            colour[v] = c 
            if graphColour(graph, m, colour, v + 1) == True: 
                return True
            colour[v] = 0

graph = [[0, 1, 1, 1], 
         [1, 0, 1, 0], 
         [1, 1, 0, 1], 
         [1, 0, 1, 0]]
colour = [0] * len(graph)
m = 3
if not graphColour(graph, m, colour, 0):
    print("无解")
else:
    print(colour)

#colour=[1,2,3,2]

旅行售货员问题

一个旅行售货员从城市 1 出发，经过其他城市一次后回到城市 1。城市之间的路径用邻接矩阵 $A$ 表示，其中，$A[i,j]$ 表示从 $i$ 到 $j$ 的有向边；$A[i,j]=10000$ 表示不存在边。

min_sum = float("inf") 
min_path = []
def TSP(graph):
    num_city = len(graph)
    path = [-1 for i in range(num_city)]
    vis = [0 for i in range(num_city)]
    path[0] = 0
    vis[0] = 1
    solveTSP(graph, path, vis, 0, 1)


def solveTSP(graph, path, vis, sum, ind):
    global min_sum
    global min_path
    num_city = len(graph)
    if ind == num_city:
        if min_sum > sum + graph[path[ind-1]][0]:
	        min_sum = sum + graph[path[ind-1]][0]
	        min_path = path.copy() + [0]
        return

    for i in range(1, num_city):
        if graph[path[ind-1]][i] < 10000 and vis[i] == 0:
            path[ind] = i
            vis[i] = 1
            sum += graph[path[ind-1]][i]
            solveTSP(graph, path, vis, sum, ind+1)
            path[ind] = -1
            vis[i] = 0
            sum = sum - graph[path[ind-1]][i]

graph = [
	[10000, 30, 6, 4],
	[30, 10000, 5, 10],
	[6, 5, 10000, 20],
	[4, 10, 20, 10000]
]

TSP(graph)

print(min_sum,min_path) #25 [0, 2, 1, 3]

这个问题除了用回溯算法外，还可以用先进先出表等方法，想了解更多的同学可以看旅行商问题。我下面只列出其他解法的代码。

#分支与界限+先入先出表

上篇贪心算法示例

下篇分支与界限