最大子段和
问题描述 求 $n$ 个数 $a_1,a_2, \cdots,a_n$ 中,最大的子段和 $\sum_{k=i}^j a_k$ ($1 \leq i \leq j \leq n$)
问题分析
之前的算法:
- 暴力算法:求出所有子段和,取最大值,复杂度为 $O(n^3)$
- 分治算法:有点类似于最近点对问题。先分成左右两段,求左右内各自的最大子段和,再求中间往两边的子段的最大和,从这三个和中取最大值作为最大子段和,复杂度为 $O(n\log n)$
动态规划算法:我们将所有最后一个元素为 $a_i$ 的子串和中最大的记为 $MS(i)$($MS$ 表示 Maximum Sum),那么显然 $MS(i)=\max { MS(i-1)+a_i, a_i }$,于是我们只需要从前往后算,求出所有的 $MS(i)$,然后取最大值即可。这个算法包括两个长度为 $n$ 的遍历,并且这两个遍历可以合并为一个,所以复杂度仅为 $O(n)$。
def MaxSum(arr):
int sum = 0, MS = 0
for i in range(len(arr)):
if MS>0:
MS+=a[i]
else
MS=a[i]
if MS>sum:
sum=MS
return sum
凸多边形最优三角剖分
问题描述 用 $n-3$ 条线将 $n$ 边的凸多边形分割为 $n-2$ 个三角形,每个三角形的权重定义为其边长之和,求所有权重和最小的划分。
问题分析
我们需要确定 $n-3$ 条线。
多边形游戏
问题描述
游戏设置:一开始有一个 $n$ 边形,每个顶点有一个数字,每一条边有一个运算符(+ 或 ×)
游戏过程:先删除一条边,然后重复下面步骤:选择一条边,计算左右顶点在边的运算符下的结果,然后删除左右顶点和这条边,用一个新的点代替,点的数字即运算结果。直到只剩一点。最后的数就是分值。
问题分析
设多边形为 $op[1]$,$v[1]$,$op[2]$,$v[2]$,……,$op[n]$,$v[n]$,
流水作业调度
问题描述 $n$ 个作业在 2 台机器 $M_1,M_2$ 上加工,每个作业先在 $M_1$ 上加工,花费 $a_1$ 时间,然后在 $M_2$ 上加工,花费 $a_2$ 时间。确定这 $n$ 个作业的最优加工顺序,使得所花费时间最少。
问题分析
显然 $M_1$ 是不会出现等待的情况的,而 $M_2$ 则有可能出现积压或空闲的情况。我们记积压的时间为 $t$,并记 $T(S,t)$ 是作业集合 $S$ 在前面积压了 $t$ 时间的情况下的最短时间。
显然,如果是最优加工顺序,那么第一个作业加工完后,剩下的依然是最优加工顺序。那么,我们有如下递推关系:
\[T(S,t)=\min_{i \in S} \{ a_i+T(S-\{i\},b_i+\max\{t-a_i,0\} )\}\]我们对 $b_i+\max\{t-a_i,0\}$ 作一个解释。如果 $t$ 小于 $a_i$,当 $a_i$ 结束后,$M_2$ 刚好空出来,所以 $t$ 不会对 $M_2$ 的作业造成影响;但如果 $t$ 大于 $a_i$,$a_i$ 结束后 $M_2$ 还要等 $t-a_i$ 才能加工其余工件。
根据上面的递推关系已经可以得到动态规划算法,但我们依然可以进一步优化:
\[T(S,t)=a_i+a_j+T(S-\{i,j\},t_{ij})\\ \begin{align} 其中,t_{ij}&=b_j+\max\{b_i+\max\{t-a_i,0\}-a_j,0\}\\ &=b_j+b_i-a_j+\max\{\max\{t-a_i,0\},a_j-b_i\}\\ &=b_j+b_i-a_j+\max\{t-a_i,0,a_j-b_i\}\\ &=b_j+b_i-a_j-a_i+\max\{t,a_i+a_j-b_i,a_i\} \end{align}\]考虑这一项:$\max\{t,a_i+a_j-b_i,a_i\}$,由于 $t$ 是固定的,所以考虑 $\max\{a_i+a_j-b_i,a_i\}$,如果对调 $i,j$ 后 $t_{ij}$ 增大,即:
\[\begin{align} \max\{a_i+a_j-b_i,a_i\} &\leq \max\{a_i+a_j-b_j,a_j\}\\ a_i+a_j + \max\{-b_i,-a_j\} &\leq a_i+a_j + \max\{-b_j,-a_i\}\\ \min\{b_i,a_j\} &\geq \min\{b_j,a_i\} \end{align}\]我们称 $\min{b_i,a_j} \geq \min{b_j,a_i}$ 为 Johnson 不等式。如果两个作业不满足 Johnson 不等式,则对调后就能满足 Johnson 不等式,并且时间会减小。所以最优调度中,相邻两个作业必定满足 Johnson 不等式。
综上,我们可以得到作业调度的 Johnson 算法:
- 将作业分成两类:$N_1={i\vert a_i<b_i}$,$N_2={i\vert a_i\geq b_i}$
- 将 $N_1$ 中的作业按 $a_i$ 递增排序,将 $N_2$ 中作业按 $b_i$ 递jian排序
- $N_1$ 后面接 $N_2$ 就是最优调度
时间复杂度主要在于排序,所以是 $O(n\log n)$,所需空间为 $O(n)$
0-1 背包问题 KnapSack
问题描述 有 $n$ 个物品,重量和价值分别为 $w_i$ 和 $v_i$,有一个背包最大承重为 $W$,问如何装入使得背包种物品的总价值最大?
我们可以给出一个数学描述:已知两个 $n$ 元向量 $\bd{w}=(w_1,\cdots,w_n)$ 和 $\bd{v}=(v_1,\cdots,v_n)$ 要求找到一个 $n$ 元 0-1 向量 $\bd{x}=(x_1,\cdots,x_n)$,使得 $\bd{w}\bd{x}^T \leq W$,并且 $\bd{v} \bd{x}^T$ 最大。
问题分析
每个物品要么在背包里面,要么不在背包里面,所以考虑第 $n$ 个物品:
- $n$ 不在背包里面,在剩下 $n-1$ 个物品中选重量小于 $W$ 的物品。
- $n$ 在背包里面,在剩下 $n-1$ 个物品中选重量小于 $W-w_n$ 的物品。
最大价值的解必然在这两种情况里,所以我们可以写出如下递归代码:
def knapSack(W , wt , val , n):
# W-允许重量 wt-物品重量 val-物品价值 n-考虑第 n 个物品的情况
if n == 0 or W == 0 :
return 0
if (wt[n-1] > W):
return knapSack(W , wt , val , n-1)
else:
return max(val[n-1] + knapSack(W-wt[n-1] , wt , val , n-1),
knapSack(W , wt , val , n-1))
这个递归会重复计算子问题,所以我们用矩阵存储子问题的解,矩阵 $\boldsymbol{K}_{n\times W}$ 的第 $i$ 行第 $j$ 列表示:前$i$ 个物品在背包容量为 $j$ 时的最大价值解
def knapSack(W, wt, val, n):
K = [[0 for x in range(W+1)] for x in range(n+1)]
for i in range(n+1):
for w in range(W+1):
if i==0 or w==0:
K[i][w] = 0
elif wt[i-1] <= w:
K[i][w] = max(val[i-1] + K[i-1][w-wt[i-1]], K[i-1][w])
else:
K[i][w] = K[i-1][w]
return K[n][W]
上面是从底部子问题向上求解的,时间复杂度为 $O(nW)$。但是其中某些子问题对求解母问题没有帮助。所以我们换一种思路,从顶部向下求解。
def knapSackRec(W,wt,val,i, K):
if i<1 or W<0:
return 0
if K[i][W] != -1:
return K[i][W]
if wt[i-1]>W:
K[i][W]=knapSackRec(W,wt,val,i-1,K)
return K[i][W]
else:
K[i][W]=max(val[i-1]+knapSackRec(W-wt[i-1],wt,val,i-1,K),
knapSackRec(W,wt,val,i-1,K))
return K[i][W]
def knapSack(W, wt, val, n):
K = [[-1 for x in range(W+1)] for x in range(n+1)]
return knapSackRec(W,wt,val,n,K)
我们用具体数值看看。背包容量为 11,4 种物品的重量与价值如下:$w=[2,3,5,6]$,$v=[3,4,5,7]$,用第一种动态规划算法(自底向上)的执行过程如下图:
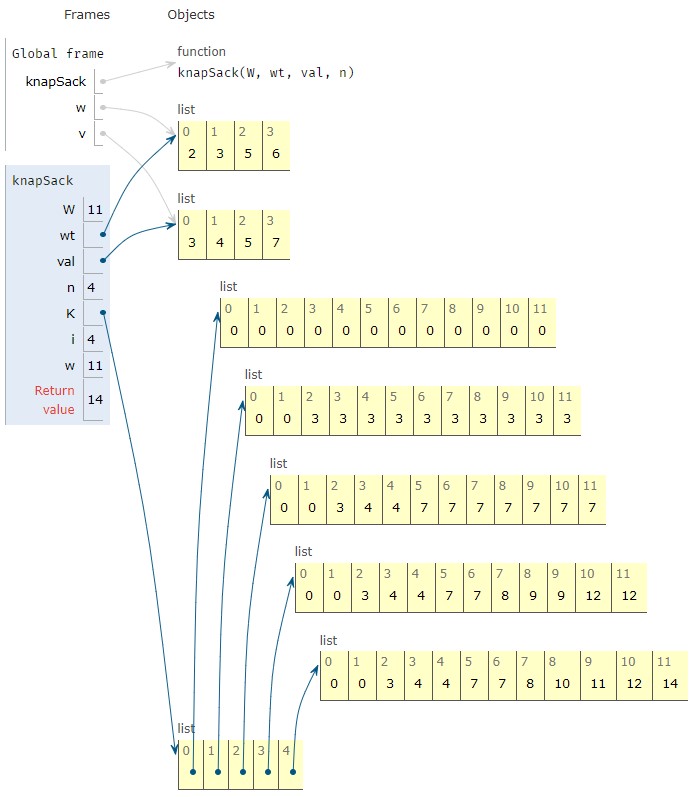
第二种动态规划算法(自顶向下)的执行过程如下图:
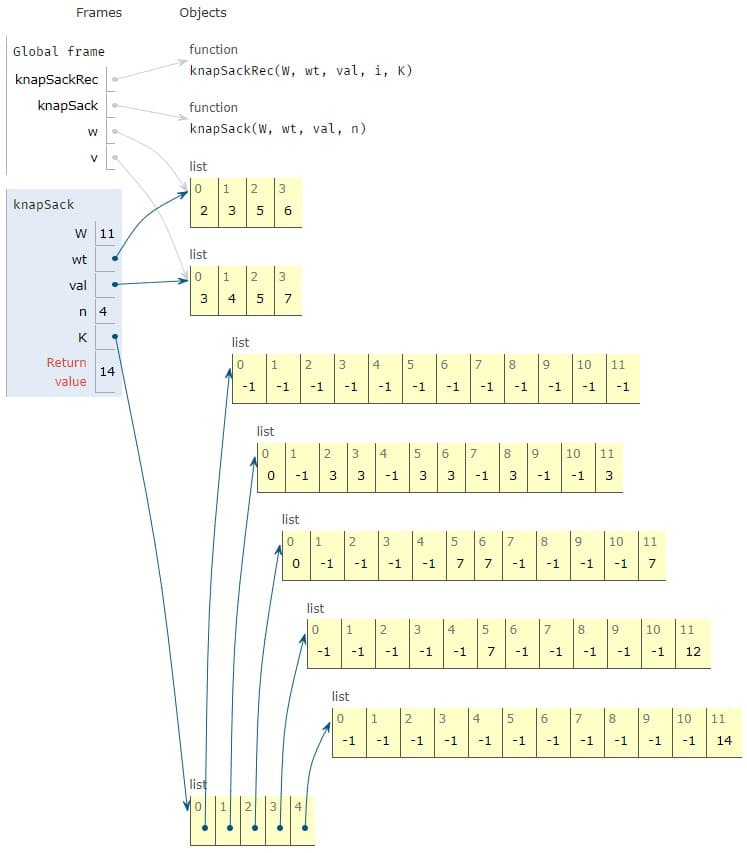
可以看出,第二种方法得到的矩阵大部分是 -1,说明这些情况是无需计算的。因此第二种方法的时间复杂度更小。但是,这种方法的复杂度比较难计算,考试如果要计算复杂度,请尽量选第一种方法。