- 分支限界法与回溯法的联系与区别
- 分支限界法的基本要素
- 求解问题的特点/回溯法问题的解空间/解空间树
- 分支限界的解空间树搜索策略/剪枝函数等 两类重要的数据结构
- FIFO队列,优先队列(最大/最小堆)
- 具体算法
- 0-1背包问题、旅行售货员问题、批处理作业调度
- 掌握上述具体算法相应的解空间、解空间树、所用算法框架、伪代码描述基本结构、剪枝策略等
- 给定输入,能大致描述算法的求解过程
分支与界限简介
分支与界限(branch and bound) 用于解决组合优化问题。这类问题的复杂度可能成指数增长,最坏情况下可能需要遍历所有组合。而分支与界限则可以很好地解决这些问题。
下面考虑之前提过的背包问题,之前的解法为:
- 贪心算法:只能解决分数背包问题
- 动态规划——能解决 0-1背包问题,但要求物体重量为整数
- 回溯算法——能解决0-1背包问题,但会搜索出所有的可行解
回溯算法是通过 DFS(深度优先搜索)来对搜索树进行剪枝,然后再比较得到最优解。我们可以在这个基础上进一步剪枝。采用 BFS(广度优先搜索),当每搜索到一个结点,我们对这个结点之后的结果进行估计,得到一个最优上界。如果这个最优上界比当前已经搜索得到的最优解还差,那么就可以舍去这个结点及其子树。
那么最优上界要如何估计?首先,结点的父母节点是已经搜索过的,所以只能根据实际加上。而后面的结点还没搜索,为了在得到最优上界的同时不超出背包容量限制,我们采用“贪心算法”,先尽可能放单位价值大的物品,若最后还有空位,则放分数个物品来填满。最终可以得到每个结点的最优上界。
为了方便计算上界,我们将物品按单位价值排序,并以这个顺序来构造搜索树。
给出如下 python 代码:
#该代码参考了Utkarsh Trivedi的C++代码
from queue import Queue #使用队列进行 BFS
from operator import itemgetter
from copy import deepcopy
class Node(object):
def __init__(self,level,profit,bound,weight):
"""
level --> 在搜索树中的层次(当前考察的物品的索引)
profit --> 从根到当前结点的价值和
bound --> 最优上界
weight --> 从根到当前结点的重量和
"""
self.level=level
self.profit=profit
self.bound=bound
self.weight=weight
def bound(u, n, W, item):
"""
用于获取当前结点的最优上界
u --> 结点
n --> item中物品数量
W --> 总重量
item --> 物品
"""
if u.weight>=W: #已放满
return 0
profit_bound = u.profit
j = u.level+1
totweight=u.weight
# 先尽可能放单位价值高的物品
while (j<n) and (totweight+item[j][0]<=W):
totweight += item[j][0]
profit_bound += item[j][1]
j+=1
# 最后用分数个物品填满
if j<n:
profit_bound += (W-totweight)*item[j][1]/item[j][0]
return profit_bound
def knapSack(W, item):
#按单位价值排序
n=len(item)
for i in range(n):
item[i].append(item[i][1]/item[i][0])
item=sorted(item, key=itemgetter(2),reverse=True)
Q = Queue() #初始化队列
u = Node(-1,0,0,0) #根结点
v = Node(0,0,0,0) #下一层结点
Q.put(u)
maxProfit=0 #初始化最大价值
# BFS
while not Q.empty():
u=Q.get()
# 已经到了最后一层
if u.level == n-1:
continue
#对 u 的子结点搜索
#将子结点的物品放入
v.level = u.level+1
v.weight=u.weight+item[v.level][0]
v.profit=u.profit+item[v.level][1]
#更新目前的最大价值
if v.weight <=W and v.profit>maxProfit:
maxProfit = v.profit
#计算最优上界
v.bound=bound(v,n,W,item)
if v.bound >= maxProfit:
#最优上界比目前最大价值大
#子树可能包含最优解
#放入队列,等待后续搜索
Q.put(deepcopy(v)) #深拷贝
#对 u 的子结点搜索
#不将子结点的物品放入
v.weight = u.weight
v.profit = u.profit
v.bound = bound(v,n,W,item)
#最大价值不变,无需计算
#计算最优上界
if v.bound >= maxProfit:
Q.put(deepcopy(v)) #深拷贝
return maxProfit
def main():
W=10
item=[[2.0,40.0],[3.14,50.0],[1.98,100.0],[5.0,95.0],[3.0,30.0]]
print("最大价值:", knapSack(W,item))
return 0
main()
代码对应的搜索树如下图:
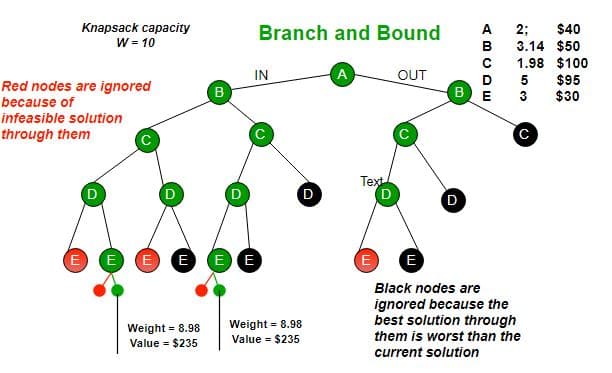
旅行商问题
前面回溯算法讲过的旅行商问题同样可以用分支与界限算法来求解。
由于我们要求的是“最短”路径,所以这里的界限是“下界”,即可能的最短路程。我们可能容易想到:最短路径 = 已有路径 + 未到结点的最短边。但考虑到在路径中,每个结点实际上与两条边相连,所以改进为:最短路径 = 已有路径 + 1/2(未到结点的最短两边)。
import heapq
class Nod:
def __init__(self, indice, traseu, mat_redusa, cost, nr):
self.indice = indice # ce valoare e rep din matrice
self.traseu = traseu # vector de perechi p(nr,cost)
self.mat_redusa = mat_redusa
self.cost = cost
self.nr = nr # nr la care s-a ajuns in arbore
def __eq__(self, other):
return (self.cost == other.cost)
def __lt__(self, other):
return (self.cost < other.cost)
def __gt__(self, other):
return (self.cost > other.cost)
# functie pentru a adauga un nod (i,j) //de la i la j
def new_nod(parent_M, traseu, nr, i, j):
# Cream mat_redusa si punem pe linia i si coloana j INF
# mat_redusa = np.copy(parent_M) # copiez frumos incet
mat_redusa = []
for l in range(n):
aux = []
for k in range(n):
aux.append(parent_M[l][k])
mat_redusa.append(aux)
for k in range(n):
if nr == 0:
break
mat_redusa[i][k] = 'INF'
mat_redusa[k][j] = 'INF'
if nr != 0:
mat_redusa[j][i] = 'INF'
cost = 0 # nu a fost calculat inca
t = []
for l in traseu:
t.append(l)
nod = Nod(j, t, mat_redusa, cost, nr)
return nod
# functii pentru a reduce matricea a.i. sa fie un 0 pe fiecare linie
def linie_reducere(M, n):
v = ['INF'] * n # in v punem valoarea minima din fiecare linie
# formam v-ul
for i in range(n):
for j in range(n):
if v[i] == 'INF':
v[i] = M[i][j]
if M[i][j] == 'INF':
continue
elif v[i] > M[i][j]:
v[i] = M[i][j]
# scadem valorile minime
for i in range(n):
for j in range(n):
if v[i] == 'INF':
continue
if M[i][j] == 'INF':
continue
M[i][j] -= v[i]
return v
# functii pentru a reduce matricea a.i. sa fie un 0 pe fiecare coloana
def coloana_reducere(M, n):
v = ['INF'] * n # in v punem valoarea minima din fiecare coloana
# formam v-ul
for i in range(n):
for j in range(n):
if v[j] == 'INF':
v[j] = M[i][j]
if M[i][j] == 'INF':
continue
elif v[j] > M[i][j]:
v[j] = M[i][j]
# scadem valorile minime
for i in range(n):
for j in range(n):
if v[j] == 'INF':
continue
if M[i][j] == 'INF':
continue
M[i][j] -= v[j]
return v
# Functie de calculat cost minim
def calc_Cost(M, n):
cost = 0
# reducem matricea
l = linie_reducere(M, n)
c = coloana_reducere(M, n)
for i in range(n):
if l[i] != 'INF':
cost += l[i]
if c[i] != 'INF':
cost += c[i]
return cost
def TSP(costM, n):
# folosim coada de prioritati ca sa retinem ce noduri sunt acum in arbore
h = []
heapq.heapify(h)
traseu = []
# cream radacina si ii calculam costul, incepem din 0
mat_redusa = []
for i in range(n):
aux = []
for j in range(n):
aux.append(costM[i][j])
mat_redusa.append(aux)
root = new_nod(mat_redusa, traseu, 0, -1, 0)
root.cost = calc_Cost(root.mat_redusa, n)
# Aduagam radacina la lista cu noduri active
heapq.heappush(h, (root.cost, root))
# Gaseste un nod activ cu cost minim
# Adauga copii lui la lista de noduri active
# Si dupa il stergem din lista
while h:
min = heapq.heappop(h)
# Dupa ce scot min, sterg tot ce era in heap si actualizez traseul
h = [] # suprasciu h-ul
heapq.heapify(h)
if min[1].indice != 0:
if len(min[1].traseu) == 0:
min[1].traseu.append((0, min[1].indice))
else:
min[1].traseu.append(
(min[1].traseu[len(traseu)-1][1], min[1].indice))
i = min[1].indice # nr pe actual
if min[1].nr == n - 1: # daca toate orasele sunt visitate
# ne intoarcem la inceput
min[1].traseu.append((i, 0))
# Afisam Traseul si costul
print("Traseul este: ")
print(min[1].traseu)
print("Costul traseului %d" % min[1].cost)
# facem pt fiecare copil al minimului
# (i,j) muchie in arbore
for j in range(n):
if min[1].mat_redusa[i][j] != 'INF':
# cream un nod si ii calculam costul
copil = new_nod(min[1].mat_redusa,
min[1].traseu, min[1].nr + 1, i, j)
copil.cost = min[1].cost + int(min[1].mat_redusa[i][j]) + \
calc_Cost(copil.mat_redusa, n)
# Adugam copiul in lista cu noduri active
heapq.heappush(h, (copil.cost, copil))
# traseu.append(min[1].indice)
# n = 4 # nr linii si coloane
# Mat = [
# ['INF', 5, 4, 3],
# [3, 'INF', 8, 2],
# [5, 3, 'INF', 9],
# [6, 4, 3, 'INF']
# ] # cost 12
# n = 5
# Mat =\
# [
# ['INF', 10, 8, 9, 7],
# [10, 'INF', 10, 5, 6],
# [8, 10, 'INF', 8, 9],
# [9, 5, 8, 'INF', 6],
# [7, 6, 9, 6, 'INF']
# ]
# # cost 34
n = 4
Mat =\
[
['INF', 2, 1, 'INF'],
[2, 'INF', 4, 3],
[1, 4, 'INF', 2],
['INF', 3, 2, 'INF']
]
# cost 8
# n = 5
# Mat =\
# [
# ['INF', 3, 1, 5, 8],
# [3, 'INF', 6, 7, 9],
# [1, 6, 'INF', 4, 2],
# [5, 7, 4, 'INF', 3],
# [8, 9, 2, 3, 'INF']
# ]
# # cost 16
TSP(Mat, n)
import math
def first_second_min(adj, i):
first, second = float('inf'), float('inf')
for j in range(len(adj)):
if i == j:
continue
if adj[i][j] <= first:
second = first
first = adj[i][j]
elif adj[i][j] < second:
second = adj[i][j]
return first, second
def solveTSP(adj, curr_bound, curr_weight, level, curr_path, visited):
global final_res
# 到达叶子结点
if level == N:
# 回到出发点
if adj[curr_path[level - 1]][curr_path[0]] != 0:
curr_res = curr_weight + adj[curr_path[level - 1]][curr_path[0]]
if curr_res < final_res:
final_path[:N+1] = curr_path[:]
final_path[N] = curr_path[0]
final_res = curr_res
return
for i in range(N):
if (adj[curr_path[level-1]][i] != 100000 and
visited[i] == False):
temp = curr_bound
curr_weight += adj[curr_path[level - 1]][i]
currFirstMin, currSecondMin = first_second_min(adj, curr_path[level - 1])
iFirstMin, iSecondMin = first_second_min(adj, i)
if level == 1:
curr_bound -= ((currFirstMin + iFirstMin) / 2)
else:
curr_bound -= ((currSecondMin +
iFirstMin) / 2)
if curr_bound + curr_weight < final_res:
curr_path[level] = i
visited[i] = True
solveTSP(adj, curr_bound, curr_weight,
level + 1, curr_path, visited)
# 恢复
curr_weight -= adj[curr_path[level - 1]][i]
curr_bound = temp
# Also reset the visited array
visited = [False] * len(visited)
for j in range(level):
if curr_path[j] != -1:
visited[curr_path[j]] = True
def TSP(adj):
N = len(adj)
curr_bound = 0
curr_path = [-1] * (N + 1)
visited = [False] * N
for i in range(N):
firstMin, secondMin = first_second_min(adj, i)
curr_bound += (firstMin + secondMin)
# 向下取整
curr_bound = math.ceil(curr_bound / 2)
# 从第 1 个城市开始
visited[0] = True
curr_path[0] = 0
solveTSP(adj, curr_bound, 0, 1, curr_path, visited)
adj = [
[10000, 30, 6, 4],
[30, 10000, 5, 10],
[6, 5, 10000, 20],
[4, 10, 20, 10000]
]
N = 4
final_path = [None] * (N + 1)
visited = [False] * N
final_res = float("inf")
TSP(adj)
print("Minimum cost :", final_res)
print("Path Taken : ", end = ' ')
for i in range(N + 1):
print(final_path[i], end = ' ')
#结果:
# Minimum cost : 25
# Path Taken : 0 2 1 3 0
最大堆与最小堆
如果一个二叉树的父结点的值总是大于等于任一子结点时,这个二叉树称为最大堆。最小堆同理。
关于如何将一个数组构造成最大堆,以及如何在最大堆中插入、删除元素,可以参考:简书:最大堆和最小堆