- 具体算法
- 二分搜索算法
- 大整数乘法
- Strassen矩阵乘法
- 归并(合并)排序
- 快速排序
- 最近点对问题
- 掌握:利用分治策略求解上述问题
- 具体问题描述
- 分治算法设计
- 伪代码描述
- 利用递归函数进行复杂度分析 算例追踪
- 算法分析题2-2, 2-3, …, 2-10;
二分查找
大整数乘积
二分
问题描述 设 X 和 Y 都是 n位 二进制整数,计算它们的乘积 XY
问题分析
我们可以使用小学所使用的方法,比如:
\[1101B\times0110B=1101B\times (10B+100B)=1001110B\]但这种方法的复杂度为 $O(n^2)$,并且不能计算超出整型范围的数。于是我们可以将 X 和 Y 分解:
\[X=A2^{n/2}+B,\quad Y=C2^{n/2}+D\] \[\begin{align} XY&=(A2^{n/2}+B)\times(C2^{n/2}+D)\\ &=AC\times2^n+(AD+BC)\times2^{n/2}+BD \end{align}\]分解后,需要做 4 次 n/2 位乘法,2 次移位 和 3 次 O(n)的加法,从而其复杂度为:
\[\begin{align} T(n)&= \begin{cases} O(1) & n=1\\ 4T(n/2)+O(n) & n>1 \end{cases}\\ &=O(n^2) \end{align}\]可以发现,复杂性并没有改进,为了减少乘法次数,我们将 XY 改写为:
\[XY=AC\times2^n+\left((A-B)(D-C)+AC+BD\right)\times2^{n/2}+BD\]只需要做 3 次 n/2 位乘法,6 次加减法和 2 次移位。最终的复杂度为:
\[\begin{align} T(n)&= \begin{cases} O(1) & n=1\\ 3T(n/2)+O(n) & n>1 \end{cases}\\ &=O(n^{\log 3})\approx O(n^{1.59}) \end{align}\]计算过程
$$ \begin{align} T(n)&=3T(n/2)+kn\\ &=3\big(3T(n/4)+kn/2\big)+kn\\ &=9\big(3T(n/8)+kn/4\big)+3kn/2+kn\\ &\cdots\\ &=3^xT(n/2^x)+\sum_{i=0}^x \left(\frac{3}{2}\right)^ikn \end{align}\\ $$ $$ 当 n=2^x 时,T(n/2^x)=O(1),故 x=\log_2 n\\ \begin{align} T(n)&=3^{\log_2 n}+\sum_{i=0}^{\log_2 n} \left(\frac{3}{2}\right)^ikn\\ &=2^{\log_2 3 \log_2 n}+2kn\cdot(\left(\frac{3}{2}\right)^{\log_2 n+1}-1)\\ &=n^{\log 3}+2kn\cdot(\frac{3n^{\log 3}}{2n}-1) &=O(n^{\log3}) \end{align} $$三分
设
\[u=u_0+u_1\cdot x_i^{n/3}+u_2\cdot x_i^{2n/3}\\ v=v_0+v_1\cdot x_i^{n/3}+v_2\cdot x_i^{2n/3}\\ w=uv=w_0\cdot x_i^{0n/3}+w_1\cdot x_i^{1n/3}+w_2\cdot x_i^{2n/3}+w_3\cdot x_i^{3n/3}+w_4\cdot x_i^{4n/3}\]则:
\[u(x_i)v(x_i)=w(x_i)\]取 $x_0=0$,$x_1=1$,$x_2=-1$,$x_3=2$,$x_4=-2$
则:
\[a=w(x_0)=(u_0+0u_1+0u_2)(v_0+0v_1+0v_2)\\ b=w(x_1)=(u_0+1u_1+1u_2)(v_0+1v_1+1v_2)\\ c=w(x_2)=(u_0-1u_1+1u_2)(v_0-1v_1+1v_2)\\ d=w(x_3)=(u_0+2u_1+4u_2)(v_0+2v_1+4v_2)\\ e=w(x_4)=(u_0-2u_1+4u_2)(v_0-2v_1+4v_2)\]$a,b,c,d,e$ 为所做的 5 个乘法,并且满足:
\[\begin{bmatrix} a\\b\\c\\d\\e \end{bmatrix}=\boldsymbol{X}_{ij} \begin{bmatrix} w_0\\w_1\\w_2\\w_3\\w_4 \end{bmatrix}\]其中,$\boldsymbol{X}_{ij}$ 为:
\[\boldsymbol{X}_{ij}= \begin{bmatrix} 1 & 0 & 0 & 0 & 0\\ 1 & 1 & 1 & 1 & 1\\ 1 & -1 & 1 & -1 & 1\\ 1 & 2 & 4 & 8 & 16\\ 1 & -2 & 4 & -8 & 16\\ \end{bmatrix}\]$\boldsymbol{X}_{ij}$ 的逆矩阵为:
\[\boldsymbol{X}_{ij}^{-1}= \begin{bmatrix} 1&0&0&0&0\\ 0 & 2/3 & -2/3 & -1/12 & 1/12\\ -5/4 & 2/3 & 2/3 & -1/24 & -1/24\\ 0 & -1/6 & 1/6 & 1/12 & -1/12\\ 1/4 & -1/6 & -1/6 & 1/24 & 1/24\\ \end{bmatrix}\]从而:
\[\begin{bmatrix} w_0\\w_1\\w_2\\w_3\\w_4 \end{bmatrix}=\boldsymbol{X}_{ij}^{-1} \begin{bmatrix} a\\b\\c\\d\\e \end{bmatrix}\]复杂度为:
\[\begin{align} T(n)&= \begin{cases} O(1) & n=1\\ 5T(n/3)+O(n) & n>1 \end{cases}\\ &=O(n^{\log5}) \end{align}\]计算过程如下:
\[\begin{align} T(n)&=5T(n/3)+kn\\ &=5\big(5T(n/9)+kn/3\big)+kn\\ &=5\big(5T(n/27)+kn/9\big)+5kn/3+kn\\ &\cdots\\ &=5^xT(n/3^x)+\sum_{i=0}^x \left(\frac{5}{3}\right)^ikn \end{align}\] \[当 n=3^x 时,T(n/3^x)=O(1),故 x=\log_3 n\\ \begin{align} T(n)&=5^{\log_3 n}+\sum_{i=0}^{\log_3 n} \left(\frac{5}{3}\right)^ikn\\ &=2^{\log_2 5 \log_2 n/\log_2 3}+\frac{3kn}{2}\cdot(\left(\frac{5}{3}\right)^{\log_3 n+1}-1)\\ &=n^{\log_3 5}+2kn\cdot(\frac{5n^{\log_3 5}}{3n}-1)\\ &=O(n^{\log_3 5})\\ \end{align}\]对比二分的大数乘法:$\log_3 5=1.465 < 1.59=\log_2 3$,可知效率有所改进。我们可以进一步分解。一般情况下,分解 $m$ 段,需要 $2m-1$ 次 $n/m$ 位乘法,$T(n)$ 满足:
\[T(n)= \begin{cases} O(1) & n=1\\ (2m-1)T(n/m)+O(n) & n>1 \end{cases}\\ T(n)=O(n^{log_m (2m-1)})\\ \lim_{m\rightarrow\infty}T(n)=O(n)(基本不太可能)\]Strassen 矩阵乘法
问题描述 设 $A$ 和 $B$ 为 $n\times n$ 矩阵,其乘积 $AB$ 中的元素 $c_{ij}$ 定义为:
问题分析
如果用定义的方法计算,则每个 $c_{ij}$ 需要做 n 次乘法,所以所有 $n\times n$ 个 $c_{ij}$ 共需要 $n^3$ 次乘法,故时间复杂度为 $O(n^3)$
我们考虑将 $AB$ 写成分块矩阵:
\[\begin{bmatrix} C_{11} & C_{12}\\ C_{21} & C_{22} \end{bmatrix}= \begin{bmatrix} A_{11} & A_{12}\\ A_{21} & A_{22} \end{bmatrix} \begin{bmatrix} B_{11} & B_{12}\\ B_{21} & B_{22} \end{bmatrix}\]类似于大数乘法,如果我们不做任何处理,按照 $C_{ij}=A_{i1}B_{1j}+A_{i2}B_{2j}$ 来计算,则需要做 8 次 $\frac{n}{2}\times\frac{n}{2}$ 的矩阵乘法,对应的复杂度为:
\[\begin{align} T(n)&= \begin{cases} O(1) & n=2\\ 8T(n/2)+O(n^2) & n>2 \end{cases}\\ &=O(n^3) \end{align}\]为了改进,Strassen 提出一种新算法,只需要做 7 次乘法:
\[\begin{align} M_1&=A_{11}(B_{12}-B_{22})\\ M_2&=(A_{11}+A_{12})B_{22}\\ M_3&=(A_{21}+A_{22})B_{11}\\ M_4&=A_{22}(B_{21}-B_{11})\\ M_5&=(A_{11}+A_{22})(B_{11}+B_{22})\\ M_6&=(A_{12}-A_{22})(B_{21}+B_{22})\\ M_7&=(A_{11}-A_{21})(B_{11}+B_{12}) \end{align}\]然后再进行加减法:
\[\begin{align} C_{11}&=M_5+M_4-M_2+M_6\\ C_{12}&=M_1+M_2\\ C_{21}&=M_3+M_4\\ C_{22}&=M_5+M_1-M_3-M_7 \end{align}\]从而时间复杂度为:
\[\begin{align} T(n)&= \begin{cases} O(1) & n=2\\ 7T(n/2)+O(n^2) & n>2 \end{cases}\\ &=O(n^{\log7})\approx O(n^{2.81}) \end{align}\]具体的计算过程可以参考大数乘法的过程。如果想要进一步提高速度,可以考虑将 $A$ 和 $B$ 分成 3×3 的分块矩阵。目前最好的算法是 Coppersmith–Winograd algorithm。

快速排序
算法描述
快速排序算法的基本思想是:
- 先从数列中取出一个数作为基准数;
- 将比这个数大的数全放到它的右边,小于或等于它的数全放到它的左边;
- 再对左右区间重复第二步,直到各区间只有一个数。
关键在于第二步。我们定义 i,j 分别指向第一个数和最后一个数。我们假设取第一个数,pivot=array[0]。
- 此时,
array[i]已保存在了pivot中,相当于在array[0]处挖了一个坑。于是我们从后往前找一个小于pivot的数array[j],填入这个坑。 - 而这时
array[j]处又有了个坑。于是我们就从前往后找一个大于pivot的数array[i],填入array[j]。 - 我们不断重复以上步骤,最终
i==j,于是我们将pivot填入array[i]
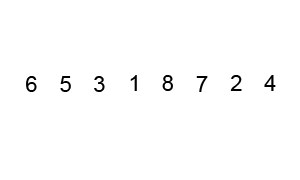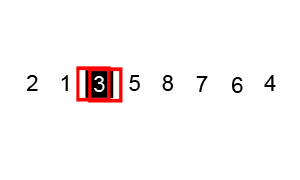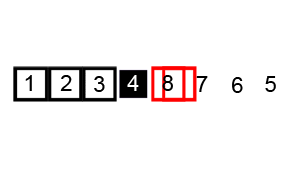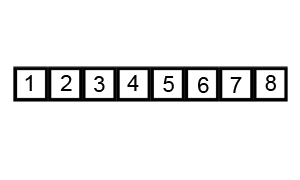
对应的 python 算法为
对应的 python 算法(点击展开)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
def partition(array, left, right):
pivot = array[left] # 基准
while left < right:
# 将右边大于基准的数换到左边
while array[right] >= pivot and left < right:
right -= 1
if left != right:
array[left] = array[right]
left += 1
# 将左边大于基准的数换到右边
while array[left] <= pivot and left < right:
left += 1
if left != right:
array[right] = array[left]
right -= 1
array[left] = pivot
return left # 返回基准位置
def quick_sort_recursion(array, left, right):
if left >= right: # 只有一个元素,直接返回
return
pivot_idx = partition(array, left, right)
if left < pivot_idx-1:
quick_sort_recursion(array, left, pivot_idx-1)
if pivot_idx+1 < right:
quick_sort_recursion(array, pivot_idx+1, right)
def quick_sort(array, left=0, right=None):
if right is None:
right = len(array) - 1
return quick_sort_recursion(array, left, right)
动态运行(加载速度很慢):
最近点对问题
问题描述 给定平面上 $n$ 个点,找到其中的一对点,使得在 $n$ 个点组成的所有点对中,该点对间距离最小。
问题分析
最简单地,我们可以计算所有点之间的距离,找出最近的点,但这样的复杂度为 $O(n^2)$。这样就会有很多多余步骤,因为假如 $A$ 与 $B$ 相隔很远,而 $C$ 与 $A$ 相隔很近,那么显然 $B$ 与 $C$ 相隔很远,那么我们就无需计算 $BC$ 距离。
我们利用分治算法解决这个问题。先根据 x 坐标的中点($x=m$)将点分为左右两个子集合 $P_L, P_R$ ,然后计算出子集合内的最小距离 $d_L, d_R$,然后取较小的那个为 $d=\min{d_L, d_R}$。

然后我们考虑两个子集之间是否有距离更小的点。我们在分割线 $x=m$ 两边取 $d$ 的宽度,然后考虑 $(m-d,m+d)$ 内是否有距离更小的点。

我们将 $(m-\delta,m+\delta)$ 内的点按纵坐标排序,然后我们寻找里面距离最短的点。这里我们无需计算所有的距离,我们只需要计算一个点与后面6个点之间的距离(这里面必然包含最短距离,因为我们考虑在)

c代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
// A divide and conquer program in C/C++ to find the smallest distance from a
// given set of points.
#include <stdio.h>
#include <float.h>
#include <stdlib.h>
#include <math.h>
// A structure to represent a Point in 2D plane
struct Point
{
int x, y;
};
/* Following two functions are needed for library function qsort().
Refer: http://www.cplusplus.com/reference/clibrary/cstdlib/qsort/ */
// Needed to sort array of points according to X coordinate
int compareX(const void* a, const void* b)
{
Point *p1 = (Point *)a, *p2 = (Point *)b;
return (p1->x - p2->x);
}
// Needed to sort array of points according to Y coordinate
int compareY(const void* a, const void* b)
{
Point *p1 = (Point *)a, *p2 = (Point *)b;
return (p1->y - p2->y);
}
// A utility function to find the distance between two points
float dist(Point p1, Point p2)
{
return sqrt( (p1.x - p2.x)*(p1.x - p2.x) +
(p1.y - p2.y)*(p1.y - p2.y)
);
}
// A Brute Force method to return the smallest distance between two points
// in P[] of size n
float bruteForce(Point P[], int n)
{
float min = FLT_MAX;
for (int i = 0; i < n; ++i)
for (int j = i+1; j < n; ++j)
if (dist(P[i], P[j]) < min)
min = dist(P[i], P[j]);
return min;
}
// A utility function to find a minimum of two float values
float min(float x, float y)
{
return (x < y)? x : y;
}
// A utility function to find the distance between the closest points of
// strip of a given size. All points in strip[] are sorted according to
// y coordinate. They all have an upper bound on minimum distance as d.
// Note that this method seems to be a O(n^2) method, but it's a O(n)
// method as the inner loop runs at most 6 times
float stripClosest(Point strip[], int size, float d)
{
float min = d; // Initialize the minimum distance as d
qsort(strip, size, sizeof(Point), compareY);
// Pick all points one by one and try the next points till the difference
// between y coordinates is smaller than d.
// This is a proven fact that this loop runs at most 6 times
for (int i = 0; i < size; ++i)
for (int j = i+1; j < size && (strip[j].y - strip[i].y) < min; ++j)
if (dist(strip[i],strip[j]) < min)
min = dist(strip[i], strip[j]);
return min;
}
// A recursive function to find the smallest distance. The array P contains
// all points sorted according to x coordinate
float closestUtil(Point P[], int n)
{
// If there are 2 or 3 points, then use brute force
if (n <= 3)
return bruteForce(P, n);
// Find the middle point
int mid = n/2;
Point midPoint = P[mid];
// Consider the vertical line passing through the middle point
// calculate the smallest distance dl on left of middle point and
// dr on right side
float dl = closestUtil(P, mid);
float dr = closestUtil(P + mid, n-mid);
// Find the smaller of two distances
float d = min(dl, dr);
// Build an array strip[] that contains points close (closer than d)
// to the line passing through the middle point
Point strip[n];
int j = 0;
for (int i = 0; i < n; i++)
if (abs(P[i].x - midPoint.x) < d)
strip[j] = P[i], j++;
// Find the closest points in strip. Return the minimum of d and closest
// distance is strip[]
return min(d, stripClosest(strip, j, d) );
}
// The main function that finds the smallest distance
// This method mainly uses closestUtil()
float closest(Point P[], int n)
{
qsort(P, n, sizeof(Point), compareX);
// Use recursive function closestUtil() to find the smallest distance
return closestUtil(P, n);
}
// Driver program to test above functions
int main()
{
Point P[] = { {2, 3}, {12, 30}, {40, 50}, {5, 1}, {12, 10}, {3, 4} };
int n = sizeof(P) / sizeof(P[0]);
printf("The smallest distance is %f ", closest(P, n));
return 0;
}