PN junction 就是 P-type 和 N-type 靠在一起,其主要特性是 rectifying current–voltage(见 fig 4-2),所以也叫 rectifier or diode,

4.1 Building Blocks of the PN Junction Theory
为了简化分析,假设 P-N 之间的浓度时突变的,这种 PN junction 称为 step junction or abrupt junction
4.1.1 Energy Band Diagram and Depletion Layer of a PN Junction
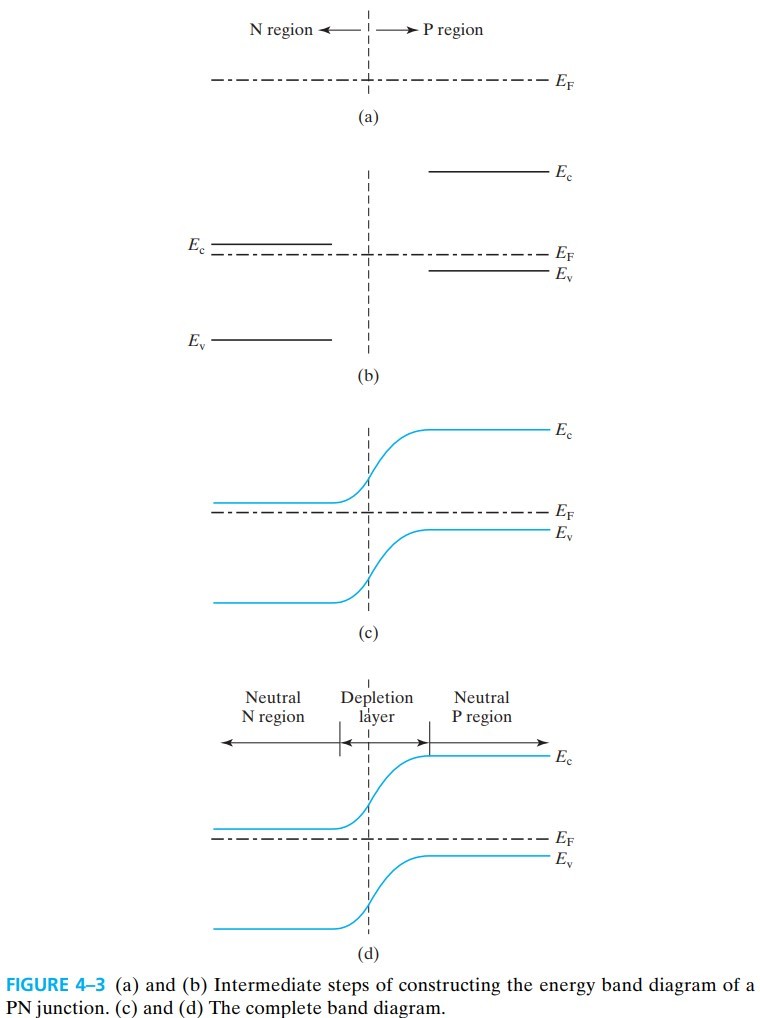
简单来说就是在一定温度下,费米能级不变,那么导带和价带就要弯曲(见 fig 4-3),这样就会形成三个区域:
- 左边:the neutral N layer
- 右边:the neutral P layer
- 中间:depletion layer 费米能级在中间,表示 $n\approx p \approx 0$
4.1.2 Built-In Potential
我们用 built-in potential $\phi_\text{bi}$ 表示能带的弯曲程度,即 $E_c$ 最高点减最低点的差值。
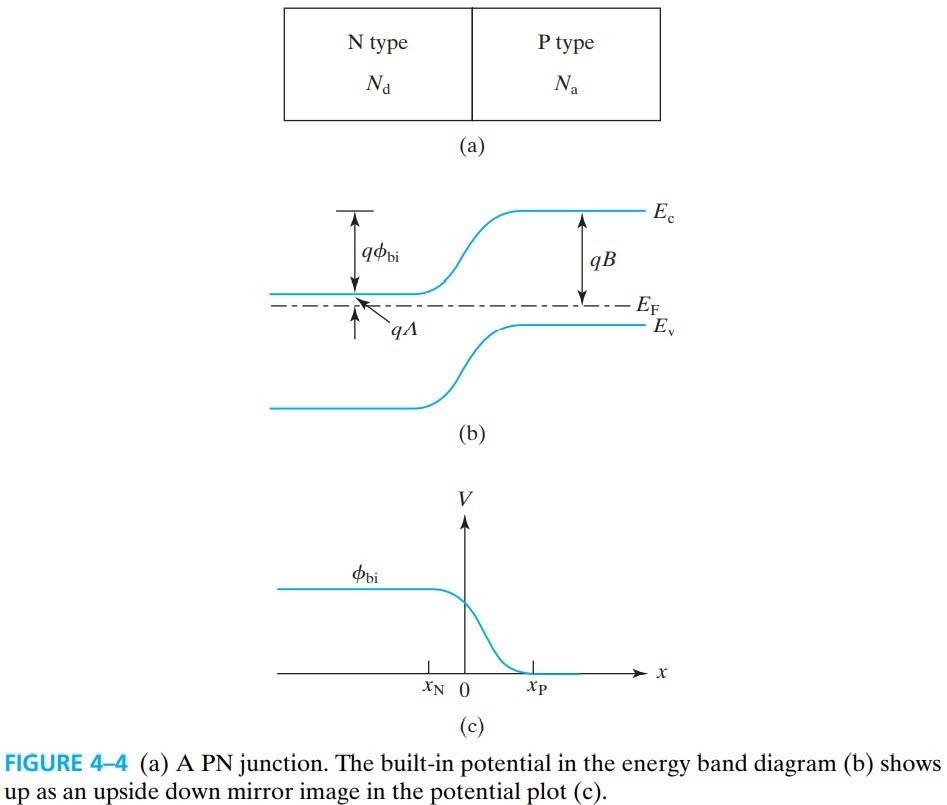
利用图 fig 4-4,可以计算出 $\phi_\text{bi}$:
\[\text{N-region} \quad n=N_d=N_c e^{-qA/kT} \Rightarrow A = \frac{kT}{q} \ln \frac{N_c}{N_d}\\ \text{P-region} \quad n=\frac{n_i^2}{N_a}=N_c e^{-qA/kT} \Rightarrow B=\frac{kT}{q}\ln \frac{N_cN_a}{n_i^2}\] \[\phi_\text{bi} = B-A = \frac{kT}{q} \ln \frac{N_dN_a}{n_i^2}\\ 其中,n_i=\sqrt{N_c N_v} e^{-E_g/2kT}\\ 所以,\phi_\text{bi} = \frac{kT}{q} \ln \frac{N_dN_a}{N_c N_v}+\frac{E_g}{q}\]从式中可以看出,如果浓度 $N_a,N_d$ 增大,则 $\phi_\text{bi}$ 也会增大。
另外,对电子来说,$E_c$ 越小,电压越高,所以内建电场的方向是从 N 指向 P。同时电压越高,电势越大,如果选取 P 区为 0 电位,那么最大的电势就是 $\phi_\text{bi}$
4.1.3 Poisson’s Equation
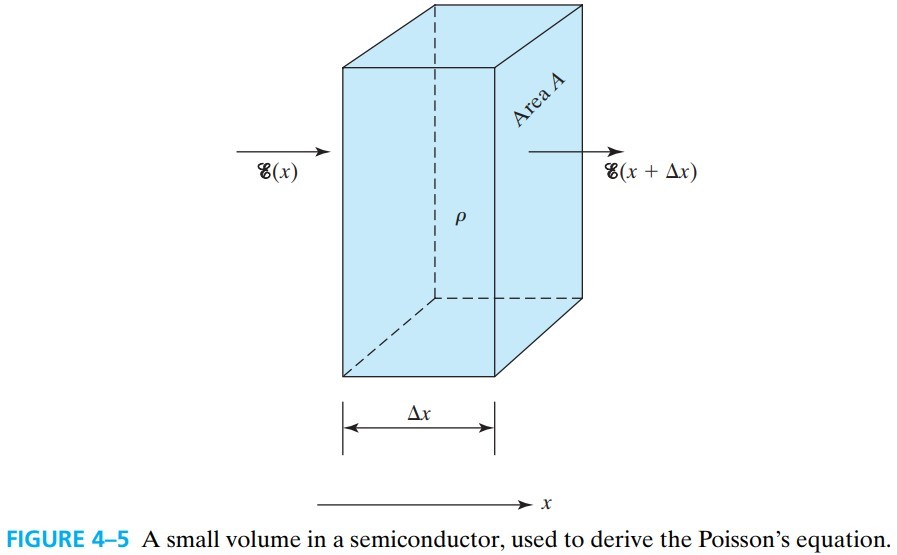
根据Gauss’s Law:$\int_V \nabla\cdot\vec{E}\dif V =\frac{1}{\varepsilon_s}\int_V\rho\dif V$,我们可以构造上图的高斯面,得到 Poisson’s equation:
\[\begin{aligned} \mathscr{E}(x+\Delta x) \cdot A- \mathscr{E}(x) \cdot A &= \frac{\rho \Delta x A}{\varepsilon_s}\\ \frac{\mathscr{E}(x+\Delta x)- \mathscr{E}(x)}{\Delta x} &= \frac{\rho}{\varepsilon_s}\\ \frac{\dif \mathscr{E}}{\dif x} &= \frac{\rho}{\varepsilon_s}\\ \frac{\dif^2 V}{\dif x^2} = - \frac{\dif \mathscr{E}}{\dif x} &= -\frac{\rho}{\varepsilon_s} \end{aligned}\]硅的绝对介电常数为 $\varepsilon_s=12\varepsilon_0$,$\varepsilon_0=8.854 × 10^{-12} \text{F/m}$
利用 Poisson’s equation,我们可以分析 depletion layer 的情况。
4.2 Depletion-Layer Model
4.2.1 Field and Potential in the Depletion Layer
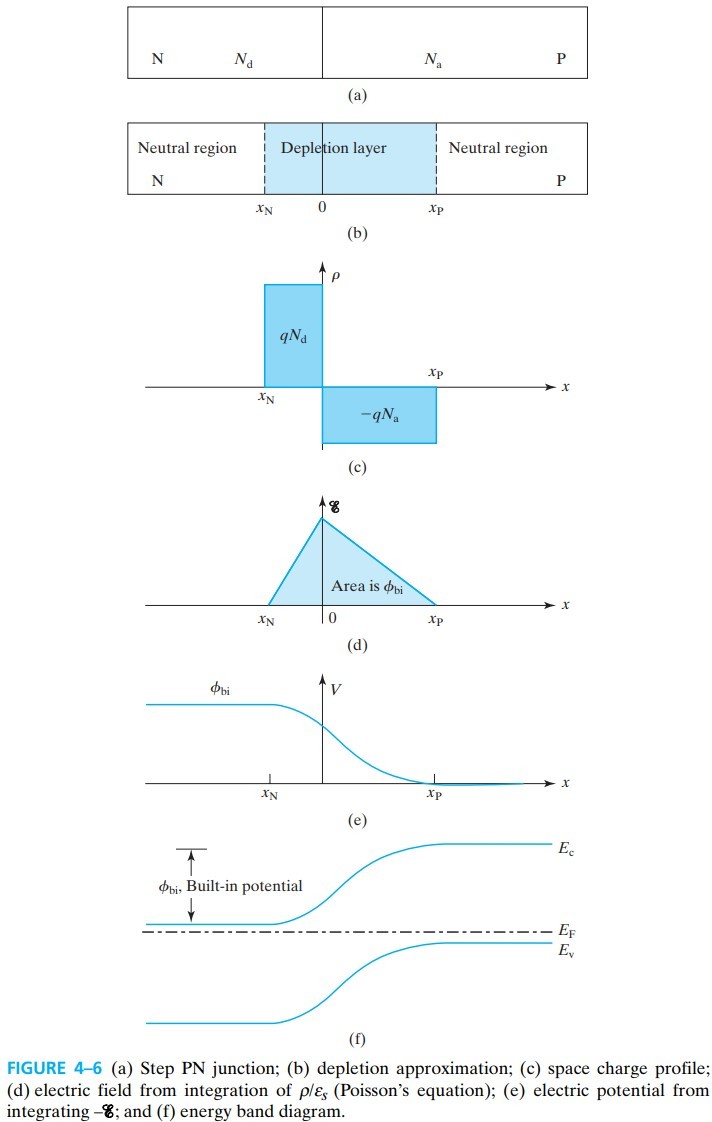
本节的任务就是对上图进行一个解释。上图描述的是 depletion layer 的情况。我们将 PN 分界面处定为 $x=0$。
在反型层中($x=0$ 附近),$n,p$ 几乎相互抵消,只剩下带正电的 donor 离子,和带负电的 accepter 离子。利用泊松方程,可以得到:
\[\frac{\dif \mathscr{E}}{\dif x} = \frac{\rho}{\varepsilon_s} = \begin{cases} \dfrac{-q N_a}{\varepsilon_s}\\ \dfrac{q N_d}{\varepsilon_s} \end{cases}\\ \Rightarrow \mathscr{E}(x) = \begin{cases} -\frac{q N_a}{\varepsilon_s} x +C_1 & x>0\\ \frac{q N_d}{\varepsilon_s} x +C_2 & x<0 \end{cases}\]积分引入了两个常量 $C_1,C_2$,故我们加入边界条件:电场在 $x_P,x_N$ 处为 $0$(可以看作是反型层的宽度),则:
\[\mathscr{E}(x) = \begin{cases} \frac{q N_a}{\varepsilon_s} (x_P-x) & x>0\\ \frac{q N_d}{\varepsilon_s} (x-x_N) & x<0 \end{cases}\]因为电场是连续的,所以在 $x=0$ 处,有:
\[N_a |x_P| = N_d |x_N| \tag{4.2.5}\]综上,我们可以画出 fig 4-6 的图 (c) 和 (d)。注意图 (c) 中,两个阴影面积是相等的。
另外,由于电势是电场在路径上的积分,所以对 (d) 积分得到 (e). (设 P 区为 0 电势点)
\[V(x)= \begin{cases} \frac{qN_a}{2\varepsilon_s}(x_P-x)^2 & 0\leq x \leq x_P\\ \phi_\text{bi} - \frac{qN_d}{2 \varepsilon_2}(x-x_N)^2 & x_N\leq x\leq 0 \end{cases} \tag{4.2.6}\]而对于电子来说,能带向电势高的地方弯曲,所以 (e) 上下反转得到 (f)
下面我们来考虑两种极端情况:$N_a \gg N_d$ 或 $N_d \gg N_a$,因为一边的浓度远大于另一边,所以称为 one-sided junction,前者称为 ${\rm P^+ N}$ junction,后者称为 ${\rm N^+ P}$ junction
根据公式$(4.2.5)$,容易看出浓度与宽度成反比,也就是说,反型层几乎集中在浓度低的那一边,浓度高的那边的反型层可以忽略。这种情况与后面要学的 metal-semicondutor junction 很类似,因此我们可以将高掺杂的一端看作金属。
4.2.2 Depletion-Layer Width
上面我们好像凭空引入了 $x_P,x_N$,但实际上 $x_P,x_N$ 受到两个条件的限制:
\[\begin{cases} N_a |x_P| = N_d |x_N| &电场连续\\ V(x_N)-V(x_P)=\phi_\text{bi} &电势差一定 \end{cases}\]我们先使用电势差恒定这个条件,考虑 $V(x)$ 在 $x=0$ 处的值,有:
\[\frac{qN_a}{2\varepsilon_s}x_P^2 = \phi_\text{bi} - \frac{qN_d}{2 \varepsilon_2} x_N^2\]将电场连续的条件代入上式,可以解出:
\[|x_N|=\sqrt{\phi_\text{bi}\bigg/\frac{q}{2\varepsilon_s}\frac{N_d}{N_a}\left( N_a + N_d \right)}\\ |x_P|=\sqrt{\phi_\text{bi}\bigg/\frac{q}{2\varepsilon_s}\frac{N_a}{N_d}\left( N_a + N_d \right)}\] \[\begin{aligned} |x_P| + |x_N| &= \sqrt{\frac{2 \varepsilon_s \phi_\text{bi}}{q(N_a+N_d)}} \cdot \left( \sqrt{\frac{N_d}{N_a}}+ \sqrt{\frac{N_a}{N_d}}\right) \\ &= \sqrt{\frac{2 \varepsilon_s \phi_\text{bi}}{q(N_a+N_d)}} \cdot \left( \frac{N_d}{\sqrt{N_a N_d}}+ \frac{N_a}{\sqrt{N_a N_d}}\right) \\ &= \sqrt{\frac{2 \varepsilon_s \phi_\text{bi}}{q}\left( \frac{1}{N_a}+\frac{1}{N_d} \right)} \end{aligned}\tag{4.2.8}\]我们将 $\vert x_P\vert + \vert x_N\vert$ 记为 Depletion-Layer Width $W_\text{dep}$
- If $N_a \gg N_d$, as in a ${\rm P^+N}$ junction, \(W_\text{dep} \approx \sqrt{\frac{2 \varepsilon_s \phi_\text{bi}}{qN_d}} \approx |x_N| \tag{4.2.9}\)
- If $N_d \gg N_a$, as in an $\rm{ N^+P}$ junction, \(W_\text{dep} \approx \sqrt{\frac{2 \varepsilon_s \phi_\text{bi}}{qN_a}} \approx |x_P| \tag{4.2.10}\)
再次说明了杂质浓度与宽度成反比。我们设 $N_a,B_d$ 中较小的浓度为 $N$,则上两式可统一为:
\[W_\text{dep} = \sqrt{\frac{2 \varepsilon_s \phi_\text{bi}}{qN}}\]4.3 Reverse-Biased PN Junction
前两节都在讲平衡时的情况,如果在 P 区加负电压,N 区加正电压,这种情况称为 reverse-biased。反向偏压会使得电势差加大,即:
\[\phi_\text{bi} \rightarrow \phi_\text{bi} +V_r\]代入 $W_\text{dep}$ 中可以得到:
\[W_\text{dep} = \sqrt{\frac{2 \varepsilon_s (\phi_\text{bi} +V_r)}{qN}}\]反偏电压使得 N 中的空穴流向 P,P中电子流向 N,但由于这两个都是少子,所以电流很小。从而 N、P 区的电压降 $IR$ 可以忽略,电压降全部加在 depletion layer 上。
请自己画一下此时的电荷分布、电场、电势、能带图。(tips:掺杂浓度小的一端宽度增大的幅度更大,另外,电势的斜率只取决于掺杂浓度)
4.4 Capacitance-Voltage Charateristics
我们将反偏时的 PN junction 看作一个平行板电容器:
\[C_\text{dep} = A\frac{\varepsilon_s}{W_\text{dep}} \tag{4.4.1}\]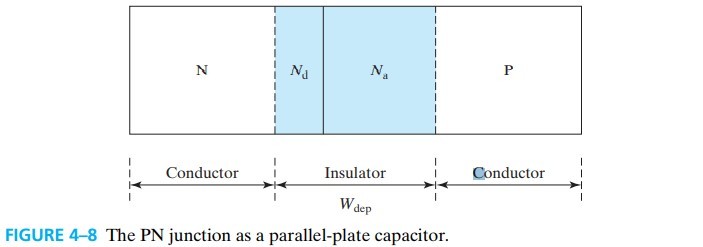
将 $W_\text{dep}$ 代入得:
\[\frac{1}{C_\text{dep}^2} = \frac{W_\text{dep}^2}{A^2 \varepsilon_s^2}=\frac{2(\phi_\text{bi}+V_r)}{q N \varepsilon_s A^2}\]从而我们可以通过测量不同反偏电压 $V_r$ 下得电容值来得到 $\phi_\text{bi}$ ($\text{intercept} = -\phi_\text{bi}$)
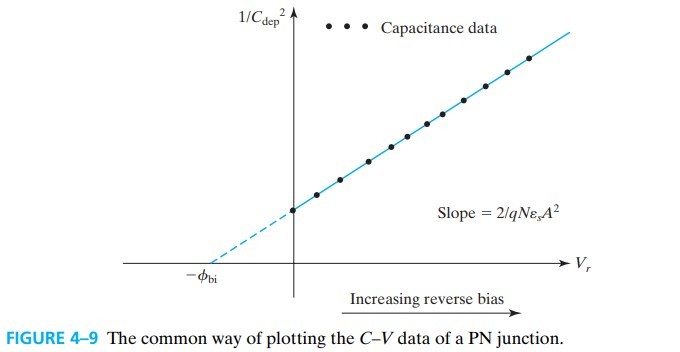
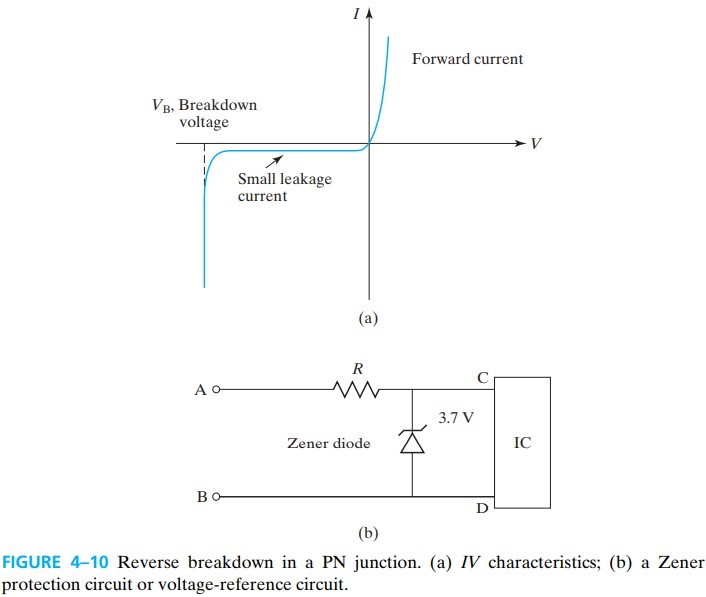
4.5 Junction Breakdown
Junction Breakdown 指的是当反偏电压大于某个值时,电流急剧增大的情况。
4.5.1 Peak Electric Field
回想 4.2.1 中得 Fig 4-6,$\mathscr{E}$ 在 $x=0$ 时取最大值,称为 peak electric field $\mathscr{E}_p$。为了简化运算,我们考虑 one-sided junction,比如 ${\rm N^+P}$ 下的 $\mathscr{E}(0)$ :
\[\mathscr{E}_p = \mathscr{E}(0)=\frac{q N_a}{\varepsilon_s} x_P = \sqrt{\frac{2 qN}{\varepsilon_s}(\phi_\text{bi}+V_r)}\]当 $\mathscr{E}(0)$ 大于某个特定值 $\mathscr{E}_\text{crit}$ 时就会发生击穿。可求出击穿电压为:
\[V_B = \frac{\varepsilon_s \mathscr{E}_\text{crit}^2}{2qN}-\phi_\text{bi}\]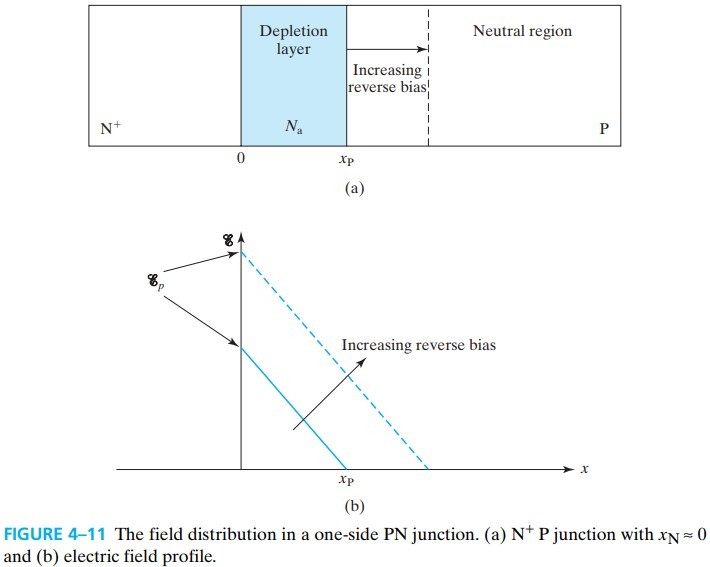
4.5.2 Tunneling Breakdown
当两端都重掺杂时,随着反偏电压加大,P区价带已经高于 N 区导带,而且他俩中间的距离很短,就会有大量电子跳过去(因为电子是波函数)
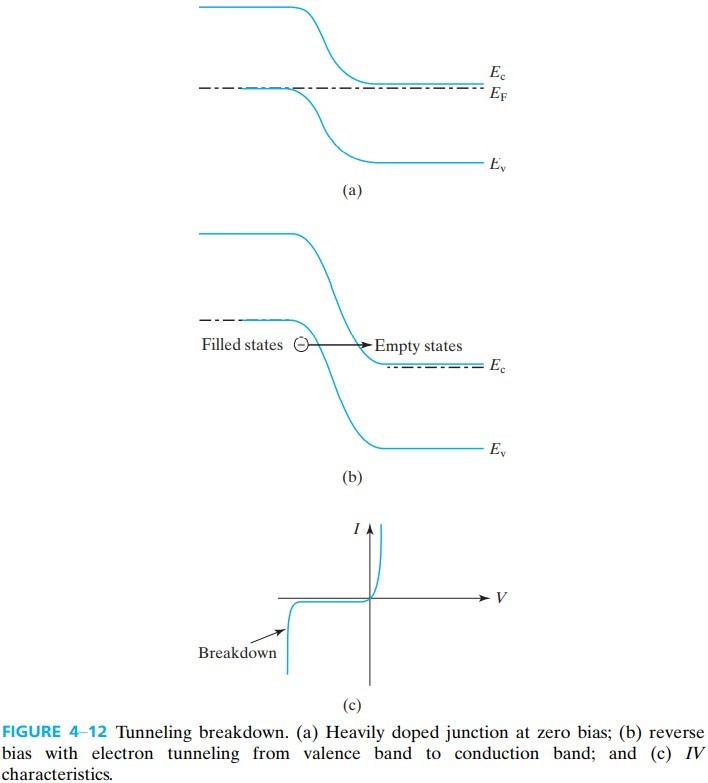
tunneling current density:$J = G e^{-H/\mathscr{E}_p}$
隧道击穿一般发生在重掺杂,击穿电压较小。
4.5.3 Avalanche Breakdown
当反偏电压很大很大时,depletion layer 中的导带电子有很大的 kinetic energy,甚至可以轰击价带电子,使其电离,这种现象称为 impact ionization
电离产生的电子-空穴对同样能加速,撞击其他电子,这个过程不断重复,像雪崩一样,所以称为 avalanche breakdown
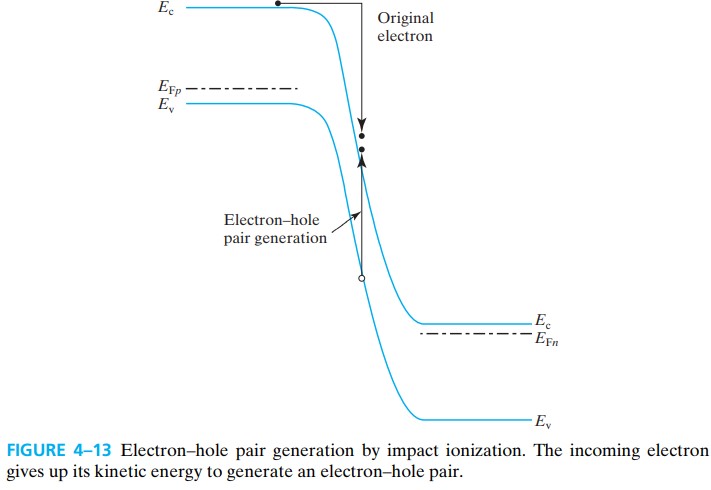
电压差 $\phi_\text{bi}+V_r$ 大到一定程度才会发生雪崩击穿。所以要增大雪崩击穿的电压,就要减小 $\phi_\text{bi}$,即减小掺杂浓度。此外,$E_g$ 越大就越难电离,所以 $E_g$ 增大也能增大雪崩击穿的电压。
4.6 Carrier Injection Under Forward Bias
正偏时,内建电场减小,电子能从 N 区扩散到 P 区,此时 P 区的少子增加,称为 minoritycarrier injection。空穴同理。
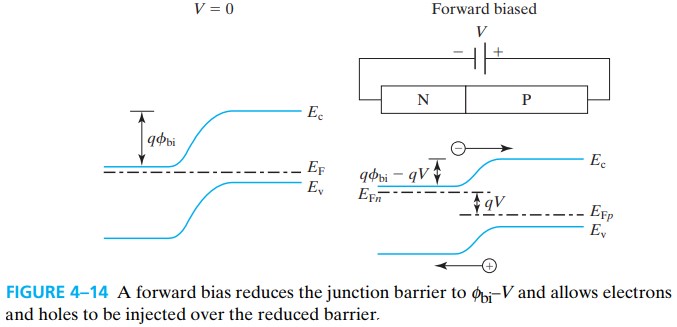
我们将无偏压下(平衡态)的少子浓度记为 $n_{P0}$(P区) 和 $p_{N0}$ (N区),那么,正偏下,在 P 区边缘:
\[\begin{aligned} n(x_P)&=N_c e^{-(E_c-E_{Fn})/kT}\\ &= N_c e^{-(E_c-E_{Fp})/kT} \cdot e^{(E_{Fn}-E_{Fp})/kT}\\ &=n_{P0} e^{(E_{Fn}-E_{Fp})/kT}\\ &= n_{P0} e^{qV/kT} \end{aligned}\]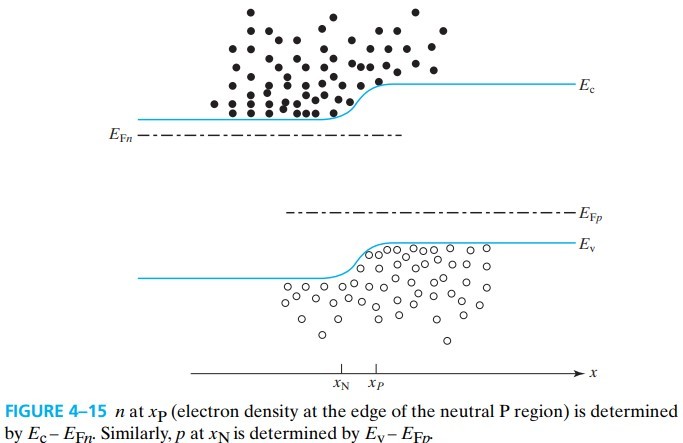
从而有 quasi-equilibrium boundary condition or the Shockley boundary condition:
\[\begin{aligned} n(x_P)&= n_{P0} e^{qV/kT}=\frac{n_i^2}{N_a} e^{qV/kT} \\ n(x_N)&= n_{N0} e^{qV/kT}=\frac{n_i^2}{N_d} e^{qV/kT} \end{aligned} \tag{4.6.2}\]或者写成 excess minority carrier concentrations:
\[\begin{aligned} n'(x_P)&= n(x_P) - n_{P0}=n_{P0} (e^{qV/kT}-1) \\ n'(x_N)&= n(x_N) - n_{N0}=n_{N0} (e^{qV/kT}-1) \end{aligned} \tag{4.6.3}\]上面的公式请牢记。我们下面会多次用到。
4.7 Current Continuity Equation
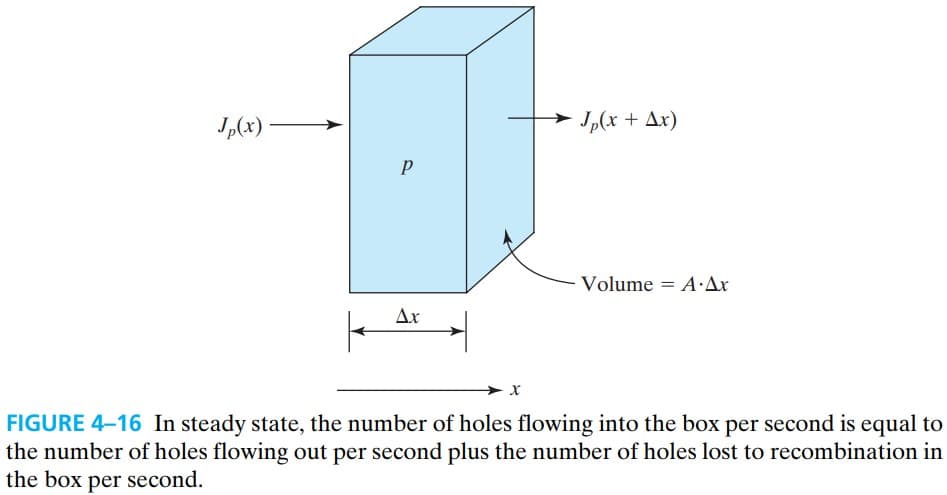
为了研究正偏时,少子在 N 和 P区的情况,我们构建上图中的模型。以在 N 区为例,在 $\Delta x$ 的长度内,有 $A\cdot \Delta x \cdot p$ 这么多的空穴,并且有 $A\cdot J_p/q$ 的空穴电流从 P 区注入,电流进去时是 $J_p(x)$,出去时是 $J_p(x+\Delta x)$,中间有一部分复合掉了,所以有:
\[A \cdot \frac{J_p(x)}{q} = A \cdot \frac{J_p(x+\Delta x)}{q} + A \cdot \Delta x \cdot \frac{p'}{\tau}\\ -\frac{J_p(x+\Delta x)-J_p(x)}{q} = q\frac{p'}{\tau}\\ -\frac{\dif J_p}{\dif x} = q\frac{p'}{\tau}\]而电流主要是以 diffusion current 为主,所以进行替换后有:
\[q D_p \frac{\dif^2 p}{\dif x^2} = q\frac{p'}{\tau_p}\]$D_p$ 是空穴的扩散系数 diffusion constant. 由于 $p=p_0+p’$,$p_0$ 取决于 $N_a$,是不变的,所以微分部分可以减去常数 $p_0$,并进行变形:
\[\frac{\dif^2 p'}{\dif x^2} = \frac{p'}{D_p\tau_p}=\frac{p'}{L_p^2} \tag{4.7.5}\\ 其中,L_p \equiv \sqrt{D_p \tau_p}\]同理,对于电子有:
\[\frac{\dif^2 n'}{\dif x^2} = \frac{n'}{L_n^2} \tag{4.7.7}\\ 其中,L_n \equiv \sqrt{D_n \tau_n}\]$L_n$ 和 $L_p$ 称为电子和空穴的 diffusion lengths
4.8 Excess Carriers in Forward-Biased PN Juntion
我们将 P 区放在左边,这样的话电流方向为正。同时,我们假设 $x_P,x_N$ 靠近于 $x=0$,因为 $x_P,x_N$ 的数量级小于我们后面要研究的量。
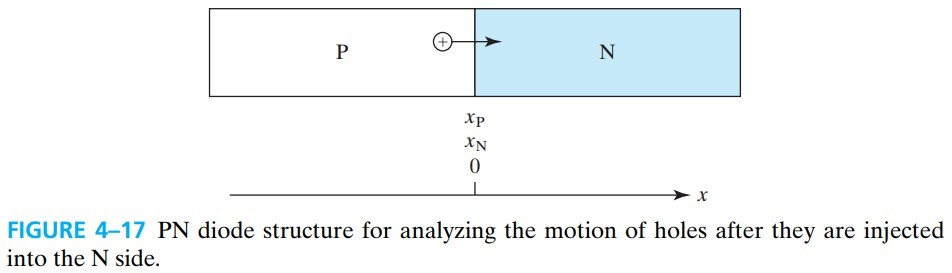
对于 N 区,要解出 $\dfrac{\dif^2 p’}{\dif x^2}=\dfrac{p’}{L_p^2}$,需要用到两个边界条件:
\[\begin{cases} p'(\infty)=0\\ p'(x_N)=p_{N0} (e^{qV/kT}-1) \end{cases}\]将上面两个条件代入通解中,可以解出:
\[p'(x)=p_{N0} (e^{qV/kT}-1)e^{-(x-x_N)/L_p}, x>x_N \tag{4.8.2}\]同理,在 P 区,可以解出:
\[n'(x)=n_{P0} (e^{qV/kT}-1)e^{(x-x_P)/L_n}, x<x_P \tag{4.8.3}\]$x_N,x_P$ 和 $L_n,L_p$ 带来的影响比较小(一般都是同一数量级),主要看 $p_{N0}$ 和 $n_{P0}$,由于掺杂越少,少子就越多,因此可以得出:轻掺杂一侧的少子注入更多。
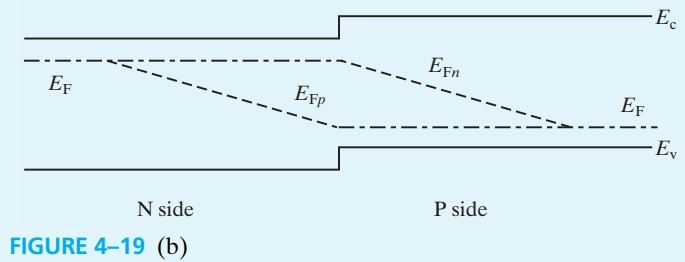
最后补充一下能带图(fig 4-19(b)),其中,斜的虚线是由于少子注入而产生的。
4.9 PN Diode I-V Characteristics
将 $(4.8.2)$ 和 $(4.8.3)$ 代入扩散电流方程,有:
\[J_{pN}= - q D_p \frac{\dif^2 p'(x)}{\dif x^2}=q \frac{D_p}{L_p} p_{N0} (e^{qV/kT}-1)e^{-(x-x_N)/L_p} \tag{4.9.1}\] \[J_{nP}= - q D_n \frac{\dif^2 n'(x)}{\dif x^2}=q \frac{D_n}{L_n} n_{P0} (e^{qV/kT}-1)e^{-(x-x_P)/L_n} \tag{4.9.2}\]根据电流连续性方程,电流处处相等,所以总电流为:
\[\begin{aligned} J &= J_{pN}+J_{nP}\\ &= \left( q \frac{D_p}{L_p} p_{N0}+q \frac{D_n}{L_n} n_{P0} \right) (e^{qV/kT}-1)\\ \end{aligned} \tag{4.9.3}\] \[I=I_0 (e^{qV/kT}-1) \tag{4.9.4}\] \[I_0=A \cdot q n_i^2 \left( \frac{D_p}{L_p N_d}+\frac{D_n}{L_n N_a} \right) \tag{4.9.5}\]做一些解释:上面我们是通过算 $x=0$ 处的电流和来求总电流。因为 $x_N,x_P$ 的数量级远小于 $L_p,L_n$,所以最后的指数项就当作 1 去掉了。最后一条式中,$A$ 是diode area,$I_0$ 是 reverse saturation current 反向饱和电流。
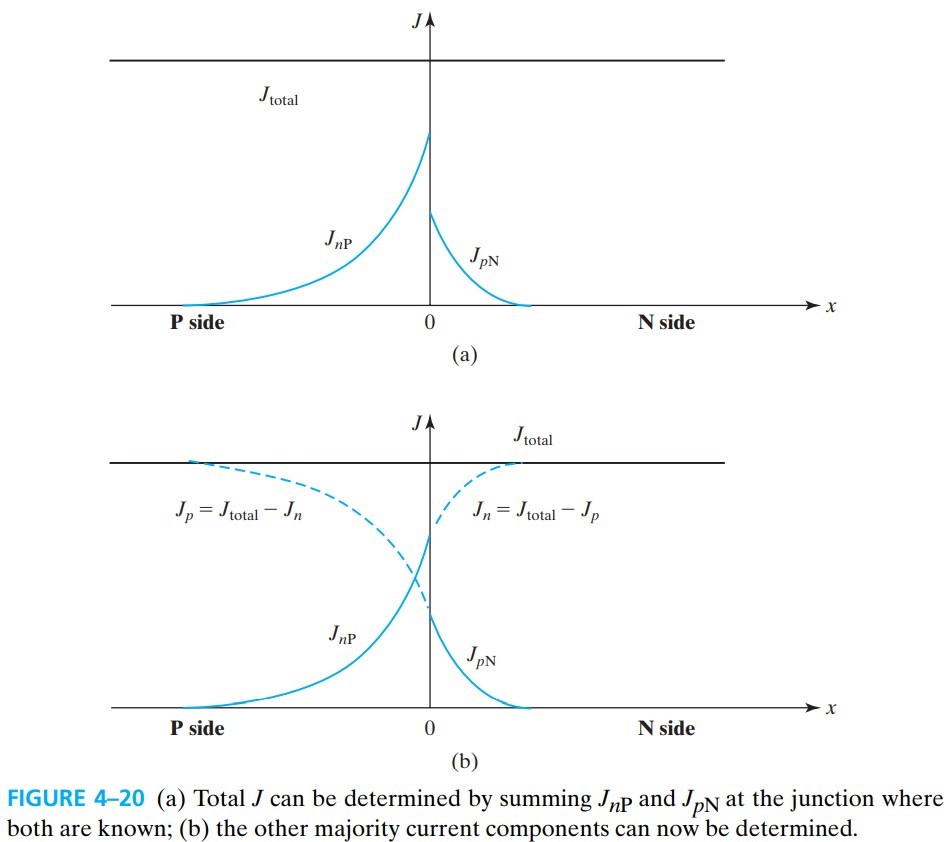
下图是电流密度分布,还是那句话:轻掺杂一侧的少子注入更多,电流越大
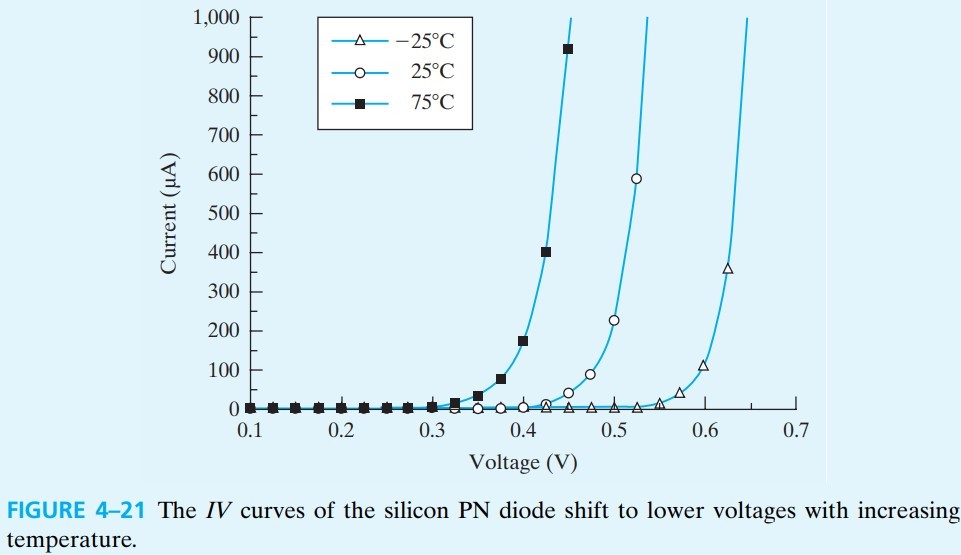
二极管的I-V特性如下图,室温下的 turnon voltage 大概是 0.6V,并且随温度升高向左移动(温度越高,$n_i$ 越大,$I_0$ 越大)
4.9.1 Contributions from the Depletion Region
上面我们忽略了 depletion layer 的影响,但实际上,载流子在耗尽层存在复合。我们将耗尽层对电流的影响称为:SCR current 或 space-charge region current(空间电荷区电流)
在空间电荷区,我们有:
\[\begin{aligned} pn &= N_c N_v e^{-(E_c-E_v)/kT} e^{-(E_{F_p}-E_{F_n})/kT}\\ &=n_i^2 e^{qV/kT} \end{aligned}\]因为没办法求出耗尽层中的 $n,p$ 分布,我们只知道当 $n \approx p \approx n_i e^{qv/2kT}$ 时复合率最大,所以复合率大概是:
\[\text{Net recombination rate per unit volume} = \frac{n_i}{\tau_\text{dep}}\left( e^{qV/2kT}-1 \right)\]$\tau_\text{dep}$ is the generation/recombination lifetime in the depletion layer.(不太清楚这是啥,总之题目会给吧),后面减 1 是为了在没有偏压时,净复合率为 0.
由于在耗尽层中产生的电子-空穴对受内建电场的影响,产生的电流方向与外电流的方向相反,所以复合「反而」对总电流有正的贡献😮,从而修正后的电流为:
\[I=I_0 (e^{qV/kT}-1) + A \frac{ q n_i W_\text{dep}}{\tau_\text{dep}}\left( e^{qV/2kT}-1 \right) \tag{4.9.4}\]第二项是 SCR current。因为存在这一项,所以注意看下图的 data,在 $I<10^{-7} \text{A}$ 时,斜率是 120mV/decade,而非 60mV/decade
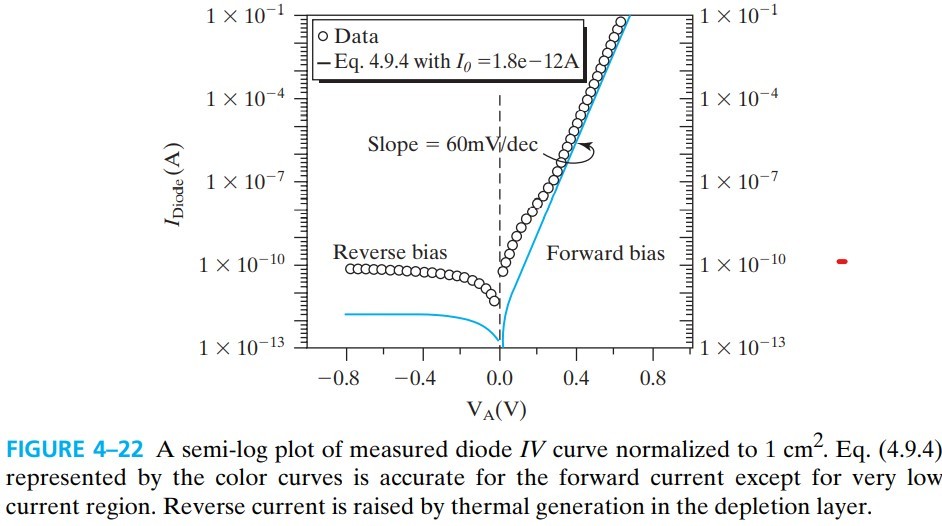
同时,reverse leakage current 反向饱和电流为:
\[I_\text{leakage} = I_0+A \frac{q n_i W_\text{dep}}{\tau_\text{dep}} \tag{4.9.10}\]4.10 Charge Storage
因为 PN diode 在正偏时存在少子注入,也就是说它有过剩载流子,相当于可以存储电荷,这称为 charge storage。显然注入的越多,存得越多,所以 $Q \propto I$,在稳态下,注入率=复合率,即:
\[I=Q/\tau_s \tag{4.10.1}\\ Q=I\tau_s\]$\tau_s$ is called the charge-storage time. In a one-sided junction, $\tau_s$ is the recombination lifetime on the lighter-doping side, where charge injection and recombination take place.
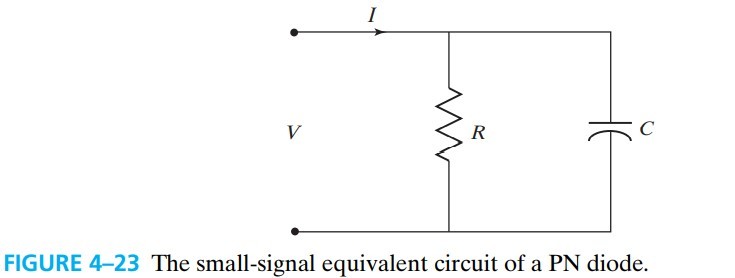
4.11 Small-Signal Model of the Diode
diode 在高频小信号电路中等效为 RC 并联:
\[G \equiv \frac{1}{R} = \frac{\dif I}{\dif V} = \frac{q}{kT} I_0 e^{qV/kT} = I_\text{DC} / \frac{kT}{q} \tag{4.11.1}\] \[C = \frac{\dif Q}{\dif V}=\tau_s \frac{\dif I}{\dif V} = \tau_s I_\text{DC} / \frac{kT}{q} \tag{4.11.2}\]室温下,$G=I_\text{DC}/26\text{mV}$. 从上两式可以看出,RC 延迟就是 charge storage time $\tau_s$,所以这个电容也称为 diffusion capacitance 或 charge-storage capacitance. 书上还说可以加上 $C_\text{dep}=A\varepsilon_s/W_\text{dep}$
4.12~4.15 略
主要讲的是一些应用。
4.16 Schottky Barriers
two kinds of metal–semiconductor junction:
- Schottky diodes: metal and lightly doped semiconductors
- ohmic contacts:metal and heavily doped semiconductors
金属的一大特性就是“电子海洋”,即在 $E_F$ 下,电子全满;在 $E_F$ 上,电子全空。根据这个特点,我们可以像 PN junction 那样画出能带图(fig4-34):
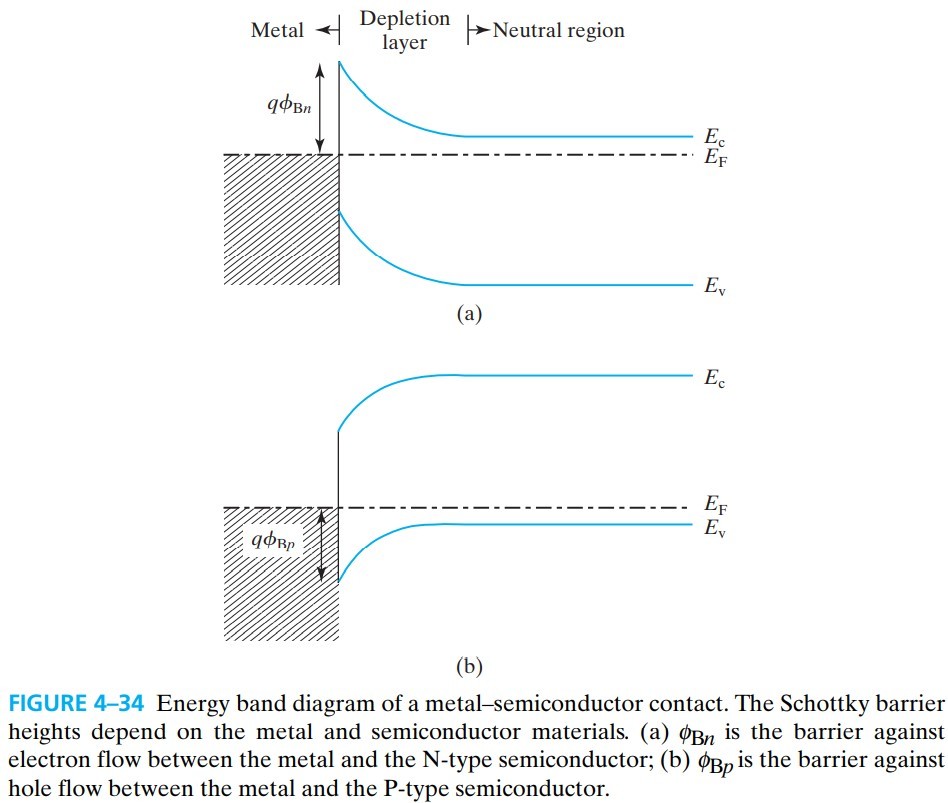
$\phi_B$ 称为 Schottky barrier height,常见金属的肖特基势垒如下表:
| Metal | Mg | Ti | Cr | W | Mo | Pd | Au | Pt |
|---|---|---|---|---|---|---|---|---|
| $\phi_{Bn}$(V) | 0.4 | 0.5 | 0.61 | 0.67 | 0.68 | 0.77 | 0.8 | 0.9 |
| $\phi_{Bp}$(V) | 0.61 | 0.50 | 0.42 | 0.3 | ||||
| $\psi_M$(V) | 3.7 | 4.3 | 4.5 | 4.6 | 4.6 | 5.1 | 5.1 | 5.7 |
肖特基势垒与 metal work function、electron affinity 的关系如下:
\[\phi_{Bn}=\phi_M -\chi_\text{Si}\]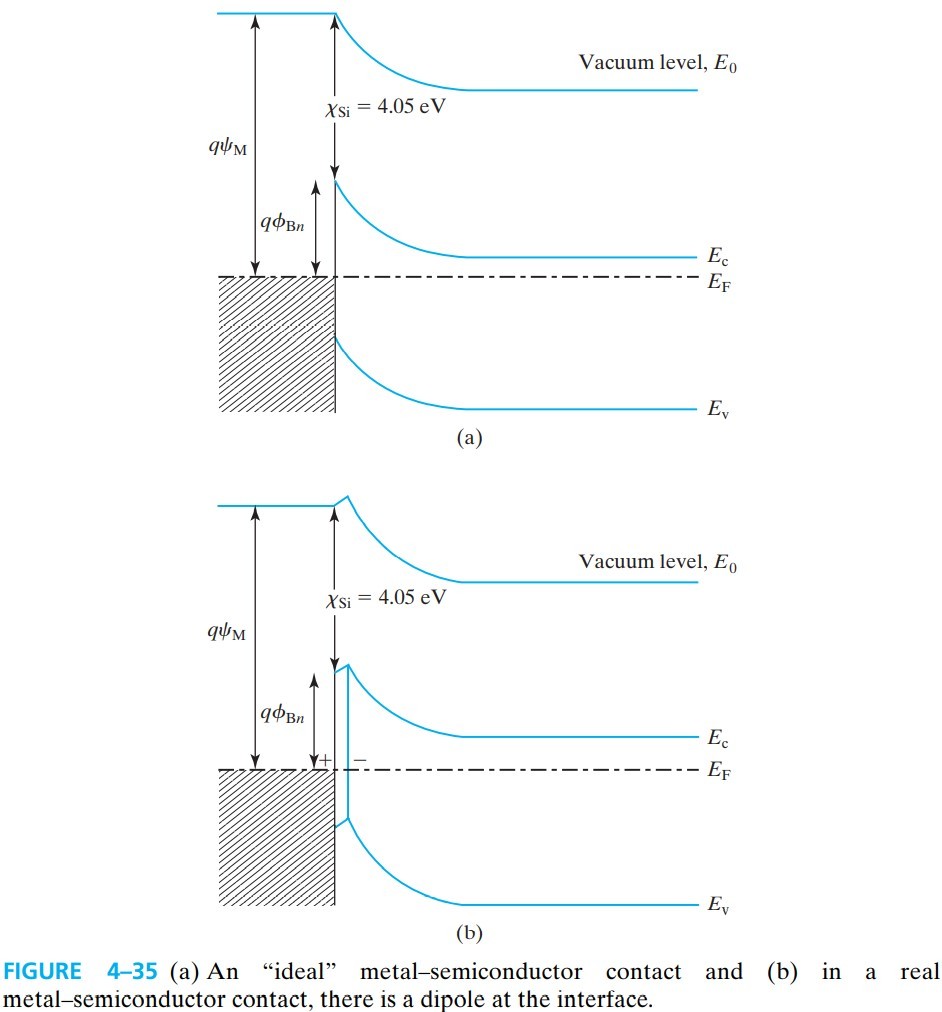
可惜实际并非如此理想,在表面处存在 dipole(极子?),它使得 $\phi_{Bn}$ 不能远离 0.7V,故修正为:
\[\phi_{Bn}=0.7 \text{V} + 0.2 (\phi_M - 4.75)\]下面来推导 $\phi_B$ 的相关公式,从图 fig 4-36a 可得到:
\[q \phi_\text{bi}=q\phi_{Bn} - (E_c-E_F)=q \phi_{Bn} - kT \ln \frac{N_c}{N_d}\]前面 4.4 已经说过可以用 C-V 求出 $\phi_\text{bi}$
\[\frac{1}{C^2}=\frac{2(\phi_\text{bi}+V)}{q N_d \varepsilon_s A^2}\]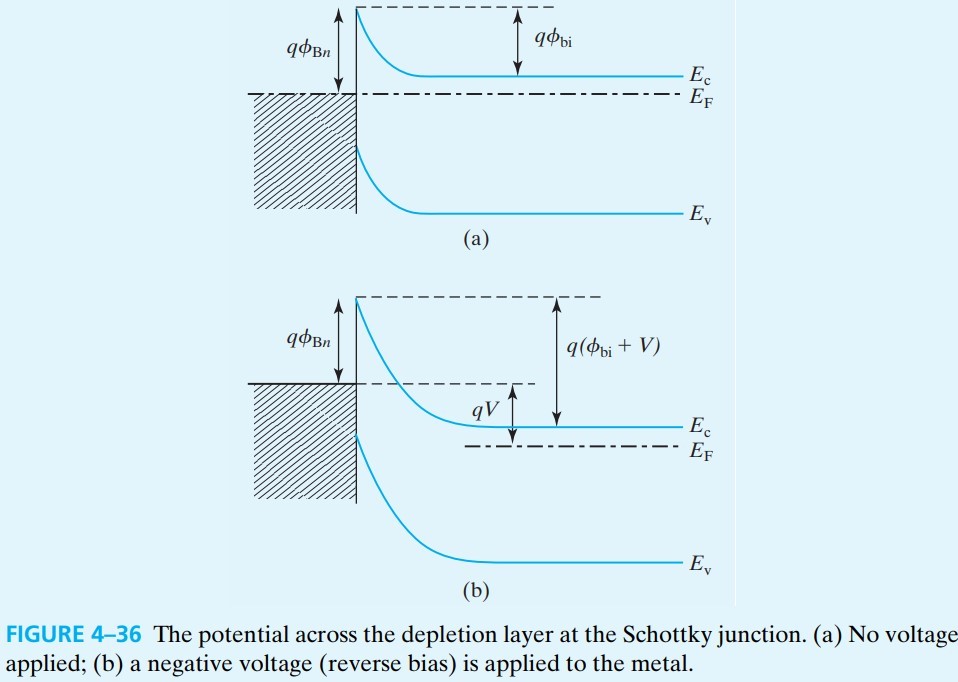
4.17 Thermionic Emission Theory
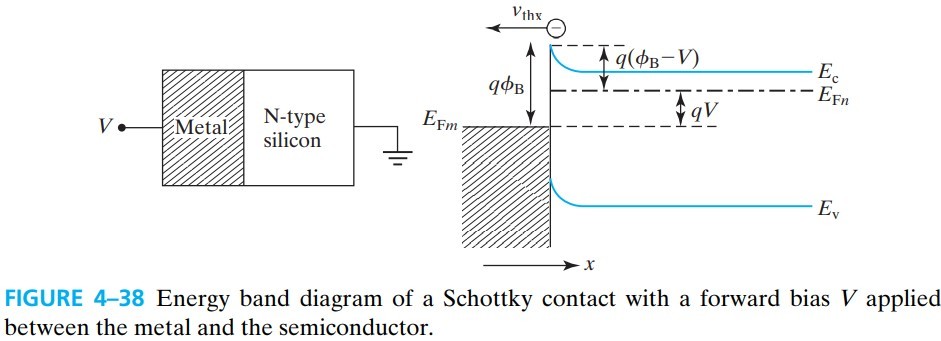
下面我们用 thermionic emission theory 热电子发射理论来分析外加电压下的电流情况。我们用 $J_{\rm S\rightarrow M}$ 表示从半导体流向金属的电流。当我们在金属上加一个正压,这种情况类似于 PN 正偏,会减小半导体一侧的势垒,从而表面处的电子浓度为:
\[n = N_c e^{-q(\phi_B-V)/kT}= 2 \left[ \frac{2 \pi m_n kT}{h^2} \right]^{3/2} e^{-q(\phi_B - V)/kT} \tag{4.17.1}\]电子做无规则热运动,其中,在 x 负方向的速度分量平均为:
\[v_\text{thx} = -\sqrt{2kT/\pi m_n}\]下标的 th 表示热,x 表示方向。从而我们可以写出电流密度:
\[J_{\rm S\rightarrow M}=-\frac{1}{2} qnv_\text{thx} = \frac{4\pi q m_n k^2}{h^3} T^2 e^{-q \phi_B /kT} e^{qV/kT}\\ \equiv J_0 e^{qV/kT} \tag{4.17.3}\]为了简化书写,我们记:
\[I_0 = AKT^2 e^{-q \phi_B /kT}\\ K=\frac{4\pi q m_n k^2}{h^3}\]$K\approx 100 {\rm A/(cm^2/K)}$ 称为 Richardson constant,
4.18 Schottky Diodes
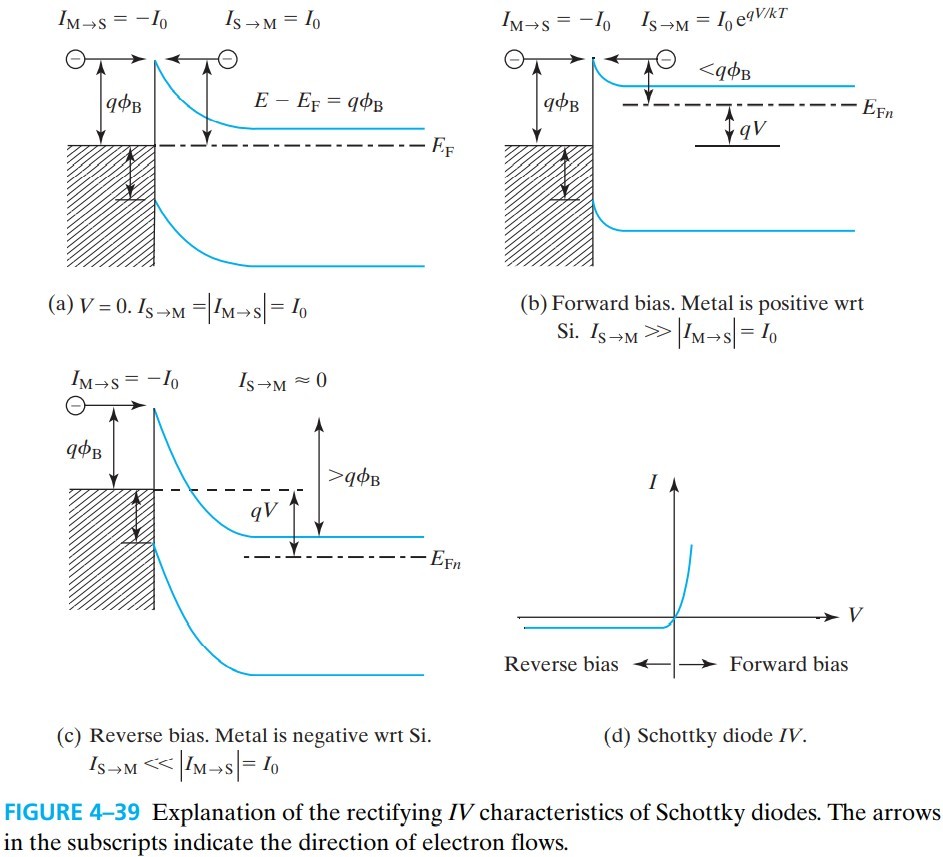
在零偏压下,金属到半导体、半导体到空穴的电流大小都等于 $I_0$,净电流为 0(fig 4-39a).
在正偏压(M正N-S负)下,半导体到空穴的电流增加 $e^{qV/kT}$ 倍,所以净电流为(fig 4-39b):
\[I = J_{\rm S\rightarrow M} + J_{\rm M\rightarrow S} = I_0 e^{qV/kT} - I_0=I_0 (e^{qV/kT}-1) \tag{4.18.4}\]上式同样可以用于求解反偏的情况。反偏电压较大的情况下,我们可以认为 $J_{\rm S\rightarrow M} \approx 0$,所以反偏电流为 $-I_0$(fig 4-39c)
4.19 Applications of Schottky Diodes
尽管肖特基和PN都有相同的 IV 表达式:
\[I=I_0 (e^{qV/kT}-1) \tag{4.19.1}\]但是,肖特基的 $I_0$ 一般比 PN 大 $10^3-10^8$ 倍,因为金属的 $\phi_B$ 比较小。因此,肖特基的电流比较大,常用于大电流整流。
另外,肖特基整流过程中的少子电流基本可以忽略,即 negligible storage of excess minority carriers,所以它的电容效应小,速度更快。
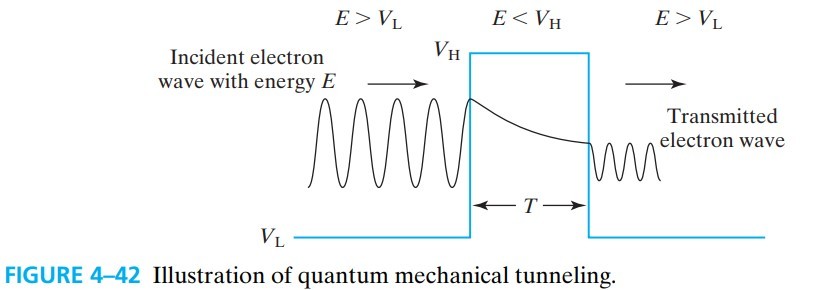
4.20 Quantum Mechanical Tunneling
大概说的是,电子波有一定概率能穿过势垒,称为 quantum mechanical tunneling。这个概率 tunneling probability 大概是:
\[P \approx \exp\left( -2 T \sqrt{\frac{8 \pi ^2 m}{h^2}}(V_H-E) \right)\]$m$ is the effective mass and $h$ is the Planck’s constant.
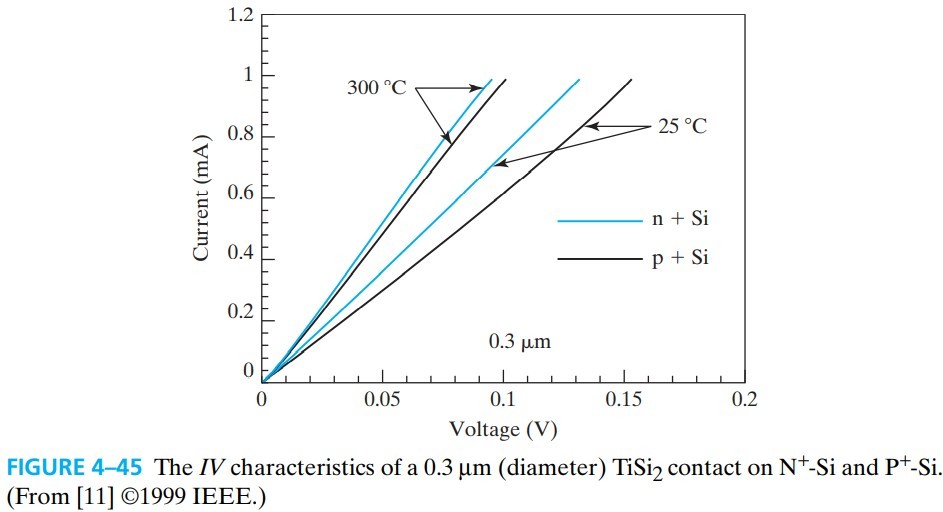
4.21 Ohmic Contacts
上一节中说过器件通过金属来连接,且接触点的电阻要够小,这样金属与半导体之间就形成了 ohmic contacts。
要达成这个目标,半导体要高掺杂,并且要足够薄(十几 $Å$,埃 $10^{-10}$),这样电子就能通过 tunneling 形成电流。
还记得上面的隧穿概率吗,在这里,势垒高度为 $\phi_{Bn}$,势垒宽度为 $W_\text{dep}/2$,所以我们可以计算出概率:
\[T \approx W_\text{dep}/2=\sqrt{\varepsilon_s \phi_{Bn}/(2qN_d)}\\ P\approx e^{-H\phi_{Bn}/\sqrt{N_d}}\\ 其中,H\equiv \frac{4\pi}{h} \sqrt{(\varepsilon_s m_n)/q}\]则电流为:
\[J_{\rm S\rightarrow M}=-J_{\rm M\rightarrow S}\approx \frac{1}{2} q N_d v_\text{thx} P\\ v_\text{thx} = -\sqrt{2kT/\pi m_n} \quad和 4.17 中的一样\]之所以要加 $\frac{1}{2}$ 是因为只有一半的电子在朝那个方向跑,另一半傻逼在往另一个方向跑。
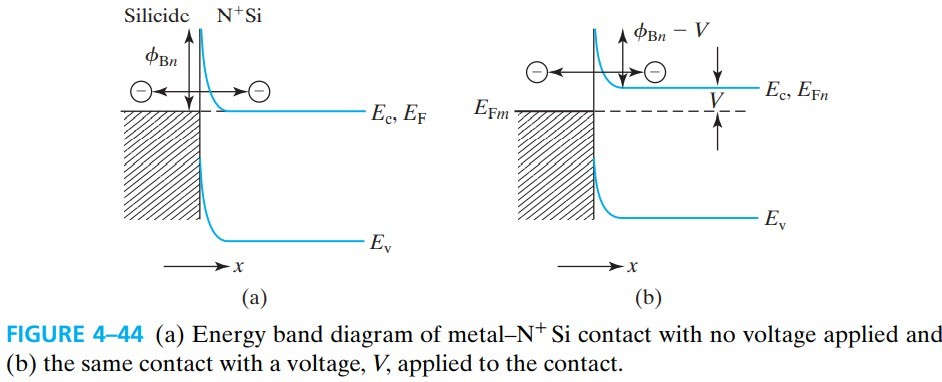
当外加偏压时(如图 4-44b),$\phi_{Bn}$ 变为 $(\phi_{Bn} - V)$,电流为:
\[J_{\rm S\rightarrow M}=\frac{1}{2} q N_d v_\text{thx} e^{-H(\phi_{Bn} - V)/\sqrt{N_d}}\]考虑在 $V=0$ 附近的小电压下,可以求出:
\[\begin{aligned} J &= \left. \frac{\dif J_{\rm S\rightarrow M}}{\dif V} \right|_{V=0}\cdot V\\ &=V \cdot \frac{1}{2} q v_\text{thx} H \sqrt{N_d} e^{-H \phi_{Bn}/\sqrt{N_d}} \end{aligned}\tag{4.21.6}\]电阻为:
\[R_c \equiv \frac{V}{J} = \frac{2 \cdot e^{H \phi_{Bn}/\sqrt{N_d}}}{q v_\text{thx} H \sqrt{N_d}}\\ \propto e^{H \phi_{Bn}/\sqrt{N_d}} \tag{4.21.7}\]这个是 $1 {\rm cm^2}$ 的电阻,称为 specific contact resistance(单位:${\rm \Omega/cm^2}$)。经过相应的替换($\phi_{Bp},m_p,N_a$)可以得到 ${\rm P^+}$ 的情况。
温度升高,会使得 $v_\text{thx}$ 增大,从而电阻减小。