MOS 代表的是 metal-oxide-semionductor,一个典型的 MOS 由三部分组成:
- semiconductor substrate
- insulator film
- metal electrode - called gate
不过也可以用 heavily doped polycrystalline silicon 来代替 metal electrode. MOS 的两种用途如下:
| MOS Capacitor | MOS Transistor |
|---|---|
 |
 </center> </center> |
我们不会直接用 MOS Capacitor,而是用 MOS Transistor。但了解 MOS Capacitor 对我们后续的学习有帮助😀。
5.1 Flat-Band Condtion and Flat-Band Voltage
照例,我们先来看看能带图:
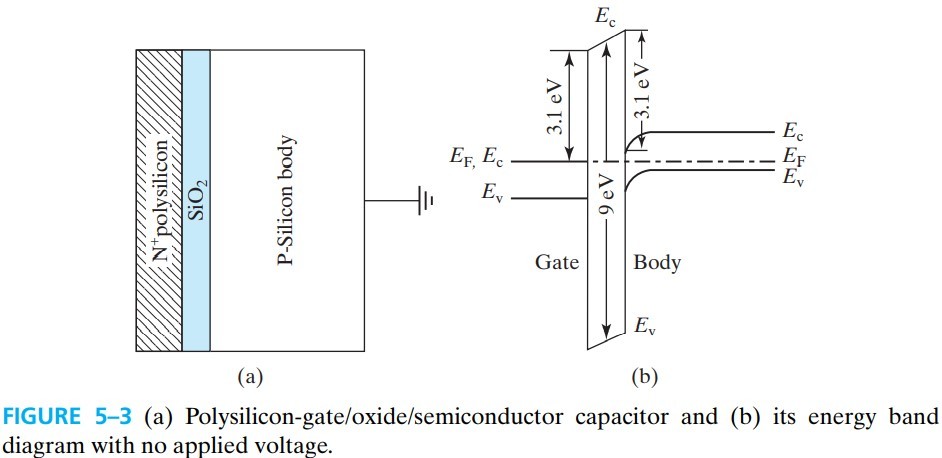
好吧,这个能带图看起来怪复杂的……我们先不看这个,先来看一种叫 flat-band condition 的情况:
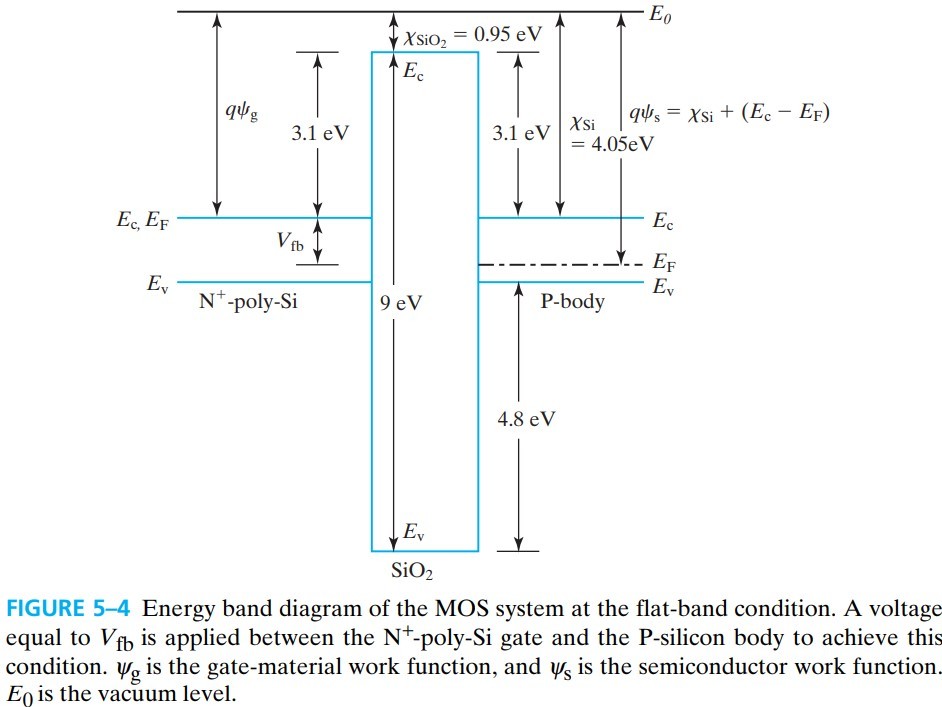
好吧,这个还是很复杂,我们一点一点分析:
- flat-band condition 是通过在 gate 上加负电压得到的。因为只有加负压才能提高电势。
- 因为能带是平的,所以
- substrate 的 the surface electric field 为 0
- ${\rm SiO_2}$ 中的 $E_c,E_v$ 也为 0,且 $E_g=9 \text{eV}$
- $E_0$ 是 vacuum level,the energy state of electrons outside the material
- 图中几个差值:
- $E_0-E_c=\chi$ 称为 电子亲合能 electron affinity,是一个材料的固定参数
- ${\rm Si}$ 的 $E_c$ 与 ${\rm SiO_2}$ 的 $E_c$ 之差称为 electron energy barrier
- ${\rm Si}$ 的 $E_v$ 与 ${\rm SiO_2}$ 的 $E_v$ 之差称为 hole energy barrier
- 为了简化分析,${\rm N^+ \; poly \; Si}$ 的 $E_F$ 与 $E_c$ 重合
- 因为 ${\rm SiO_2}$ 的禁带很宽,所以 $E_F$ 放中间哪个位置都差不多,我们干脆就不管它了
平带时所加的电压称为 flat-band voltage $V_\text{fb}$。没加电压前两边的费米能级相等,加了后存在差值,所以平带电压为:
\[V_\text{fb} = \psi_g - \psi_s \tag{5.1.1}\\ 考试请使用 (5.7.1) 的修正公式\]$\psi_g,\psi_s$ 是 gate and semi’ 的真空能级与费米能级之间的差值,称为 work function
5.2 Surface Accumulation
如果进一步减小 $V_g$,那么 gate 的能带就进一步提高,substrat 的能带就下凹(fig 5-5)
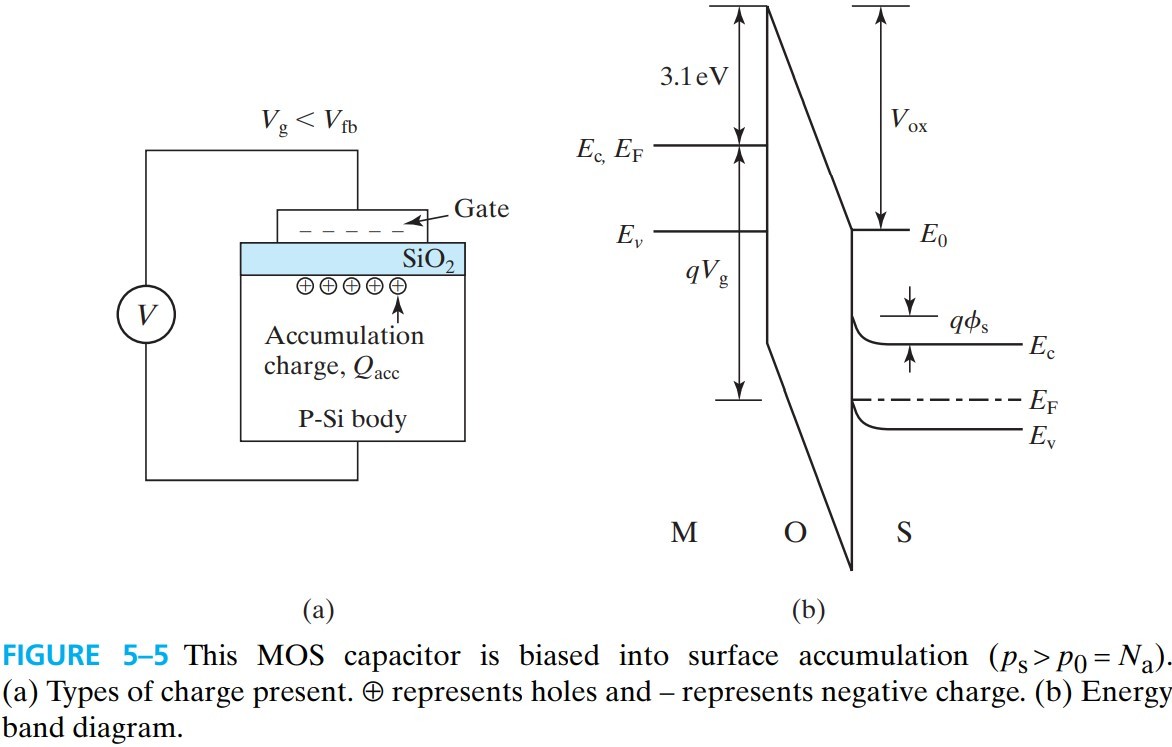
从图中注意到几件事:
- gate 的能带没弯,说明它上面几乎没电压降(毕竟金属内部没电场)
- ${\rm SiO_2}$ 上的电压 oxide voltage 为 $V_\text{ox}$,定义为 gate 减去 substrate,所以是 up toward the gate is negative(图中)
- substrate 的电压降为 $\phi_s$,并且主要集中在表面。$\phi_s$ 是 surface voltage,因为衬底是 0 电势,所以 bends upward is negative(图中),bends downword is positive.
因为衬底表面处的 $E_F$ 更靠近 $E_v$,所以表面空穴浓度为:
\[p_s = N_a e^{-q \phi_s / kT} \tag{5.2.1}\]这个浓度比内部大($\phi_s$ 为负),所以空穴在表面形成 accumulation layer,这些空穴称为 accumulation-layer holes,对应的电荷为 accumulation charge, $Q_\text{acc}$。这种情况称为 surface accumulation
这时候加在上面的总电压是多少呢?二氧化硅有分压 $V_\text{ox}$,衬底表面有分压 $\phi_s$,再加上平带电压 $V_\text{fb}$,则:
\[V_g = V_\text{fb}+\phi_s+V_\text{ox} \tag{5.2.2}\]但我们仍不清楚 $\phi_s$ 和 $V_\text{ox}$ 的值。这时候我们不妨用作一个高斯面(长度为绝缘层厚度 $T_\text{ox}$,两边面积为 $1 {\rm cm^2}$)包围绝缘层,由 Gauss’s Law 可以求出电场:
\[\mathscr{E}_\text{ox} = -\frac{Q_\text{acc}}{\varepsilon_\text{ox}}\]为什么要加负号呢?简单来讲就是电场指向负x方向。(还要考虑正负啥的烦死了啊😣)
从而可以求出绝缘层上的分压:
\[V_\text{ox} = \mathscr{E}_\text{ox} T_\text{ox} = -\frac{Q_\text{acc}}{C_\text{ox}} \tag{5.2.4}\]其中,$C_\text{ox}=\dfrac{\varepsilon_\text{ox}}{T_\text{ox}}$ 是单位面积的 oxide capacitance(是个常量),$Q_\text{acc}$ 是单位面积的 accumulation charge。
从而结合 $(5.2.1)$,有:
\[Q_\text{acc}=-C_\text{ox}(V_g-V_\text{fb}-\phi_s) \tag{5.2.5a}\]上式中的三个电压都是负的。把 $Q_\text{acc} = qp_s=q e^{-q\phi_s/kT}$ 代入,这样一来就可以解出 $\phi_s$. 但这个解实在太复杂了,而且解出来的 $\phi_s$ 很小,所以我们干脆忽略 $\phi_s$:
\[Q_\text{acc}=-C_\text{ox}(V_g-V_\text{fb}) \tag{5.2.5b}\]也就是说,MOC capacitor 就是个电容器,只不过有一个 $V_\text{fb}$ 的 shift。既然这样,那积累的电荷不能只算衬底表面电荷,而是衬底所有的电荷 $Q_\text{sub}$,从而:
\[V_\text{ox}=-Q_\text{sub}/C_\text{ox}\]5.3 Surface Depletion
反过来,如果 $V_g$ 大于 $V_\text{fb}$ 会怎么样呢?从能带图中看,在衬底表面形成了 depletion region(像 PN 结那样),所以这种情况叫 surface depletion
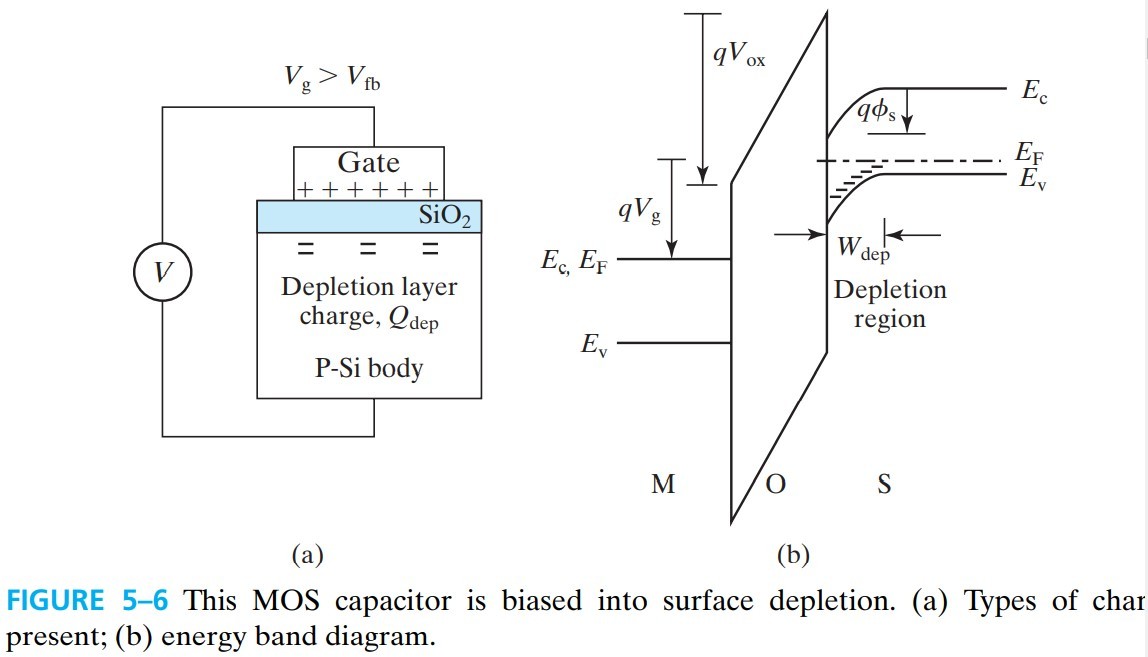
耗尽层中没有空穴,只有带负电的施主离子,不能导电,根据上面的电容公式,有:
\[V_\text{ox}=-\frac{Q_\text{sub}}{C_\text{ox}}=-\frac{Q_\text{dep}}{C_\text{ox}}=\frac{q N_a W_\text{dep}}{C_\text{ox}}\]其中,根据上一章 4.2 节的公式,有 $W_\text{dep} = \sqrt{\dfrac{2 \varepsilon_s \phi_\text{bi}}{qN}}$(但某些变量不同),所以:
\[V_\text{ox}= \frac{\sqrt{q N_a 2 \varepsilon_s \phi_s}}{C_\text{ox}} \tag{5.3.1}\] \[以及 \; \phi_s = \frac{q N_a W_\text{dep}^2}{2 \varepsilon_s} \tag{5.3.2}\]把这俩玩意代入回咱的电压关系式:
\[V_g = V_\text{fb}+\phi_s+V_\text{ox}=V_\text{fb}+\frac{q N_a W_\text{dep}^2}{2 \varepsilon_s}+\frac{q N_a W_\text{dep}}{C_\text{ox}} \tag{5.3.3}\]可以看出,$W_\text{dep}$ 与 $V_g$ 存在一定关系。通过上式可以求出 $W_\text{dep}$,进而求出 $\phi_s$,进而求出 $V_\text{ox}$
5.4 Threshold Condition and Threshold Voltage
如果进一步加大 $V_g$ 电压呢?这样能带就会弯得更厉害,使得 $V_F$ 更靠近 $E_c$,这种情况下就不是耗尽了,而是 inversion,表面处不再是 P 型,而是 N 型(电子多于空穴)。
当表面的电子 $n_s=N_a$ 时,有 $(E_c-E_F)_\text{surface}=(E_F-E_v)_\text{bulk}$,也就是下图中,$A=B$,$C=D$,这种情况称为 threshold of inversion
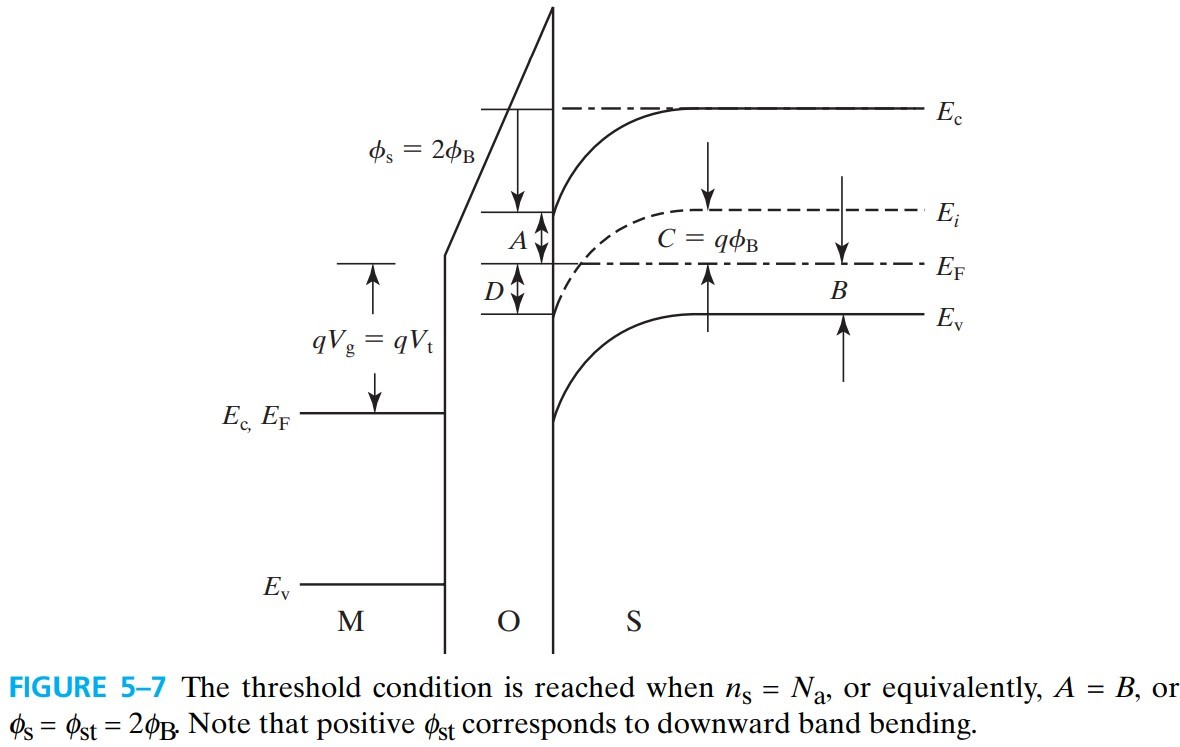
此时,表面能带的弯曲程度记为 $\phi_{st}$,从图中可以看出 $\phi_{st}=(C+D)/q=2C/q=2\phi_B$。其中,$\phi_B$ 为:
\[\begin{aligned} q\phi_B &\equiv \left. \frac{E_g}{2}-(E_F-E_v) \right\vert_\text{bulk}\\ &=k T \ln \frac{N_v}{n_i}-kT \ln \frac{N_v}{N_a}\\ &=kT\ln \frac{N_a}{n_i} \end{aligned} \tag{5.4.1}\]所以:
\[\phi_{st} = 2 \phi_B = 2 \frac{kT}{q} \ln \frac{N_a}{n_i} \tag{5.4.2}\]此时 gate 上的电压 $V_g$ 称为 threshold voltage $V_t$,可以用之前的电压关系式求出:
\[\begin{aligned} V_t &= V_\text{fb}+\phi_s+V_\text{ox}\\ &= V_\text{fb}+2 \phi_B+\frac{\sqrt{q N_a 2 \varepsilon_s 2\phi_B}}{C_\text{ox}} \end{aligned} \tag{5.4.3}\]
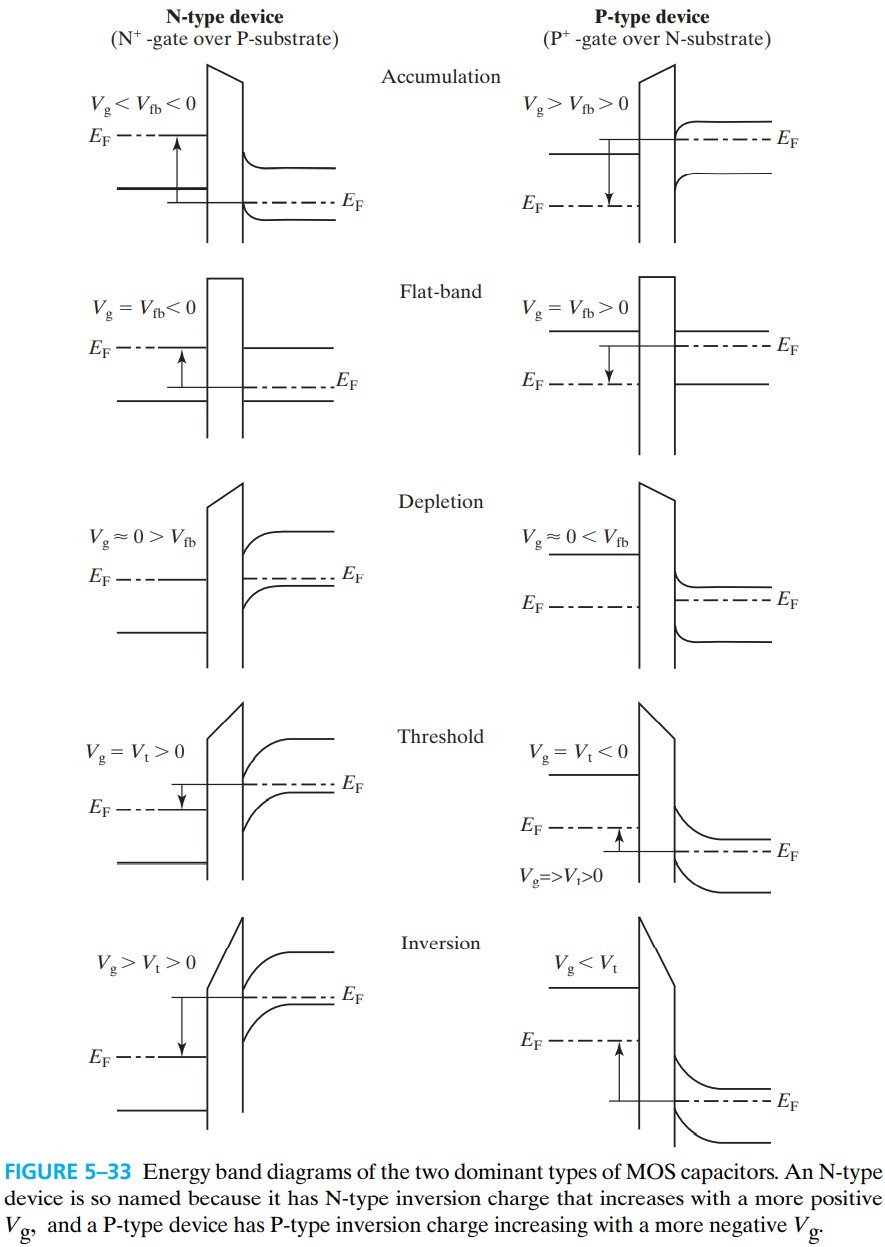
对于 N 型衬底,上述公式变为:
$$
V_t = V_\text{fb}+\phi_{st}-\frac{\sqrt{2 q N_d \varepsilon_s |\phi_{st}|}}{C_\text{ox}}
$$
$$
\phi_{st}=-2\phi_B
$$
$$
\phi_B=\frac{kT}{q}\ln \frac{N_d}{n_i}
$$
看上去式子中符号很奇怪,但实际上符号与 P 型是相反的。
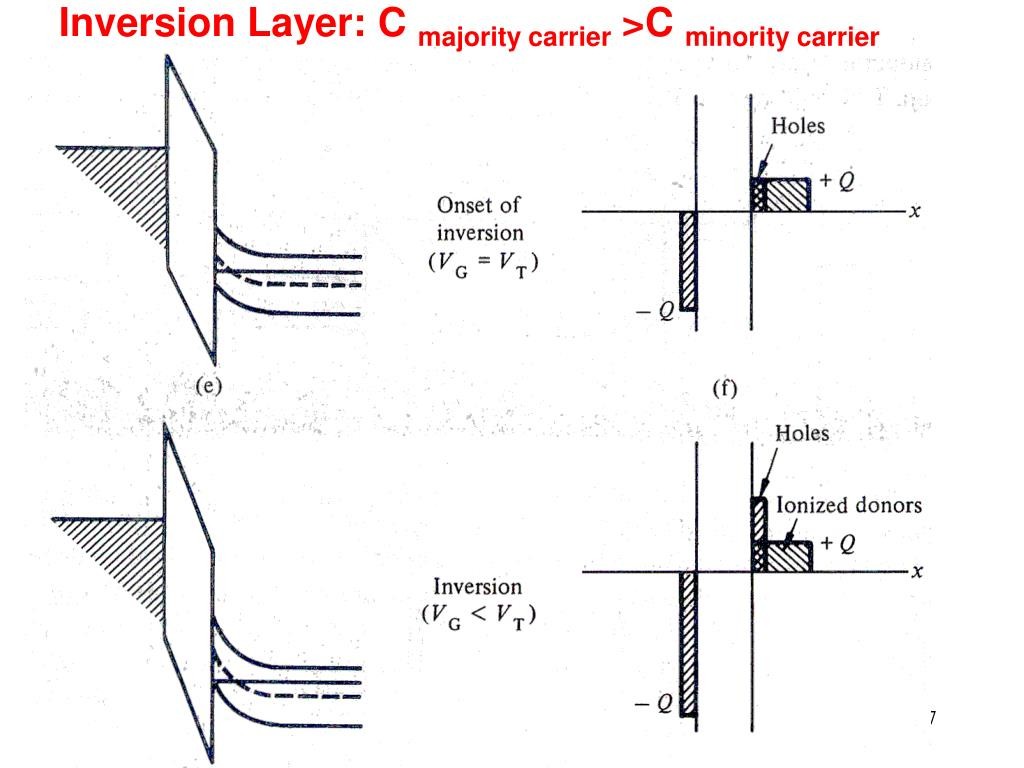
5.5 Strong Inversion Beyond Threshold
再再再次加大 $V_g$ 电压,衬底表面就会有反型层电子 inversion electrons,电荷密度 inversion charge density 为 $Q_\text{inv}$ (${\rm C/cm^2}$)。
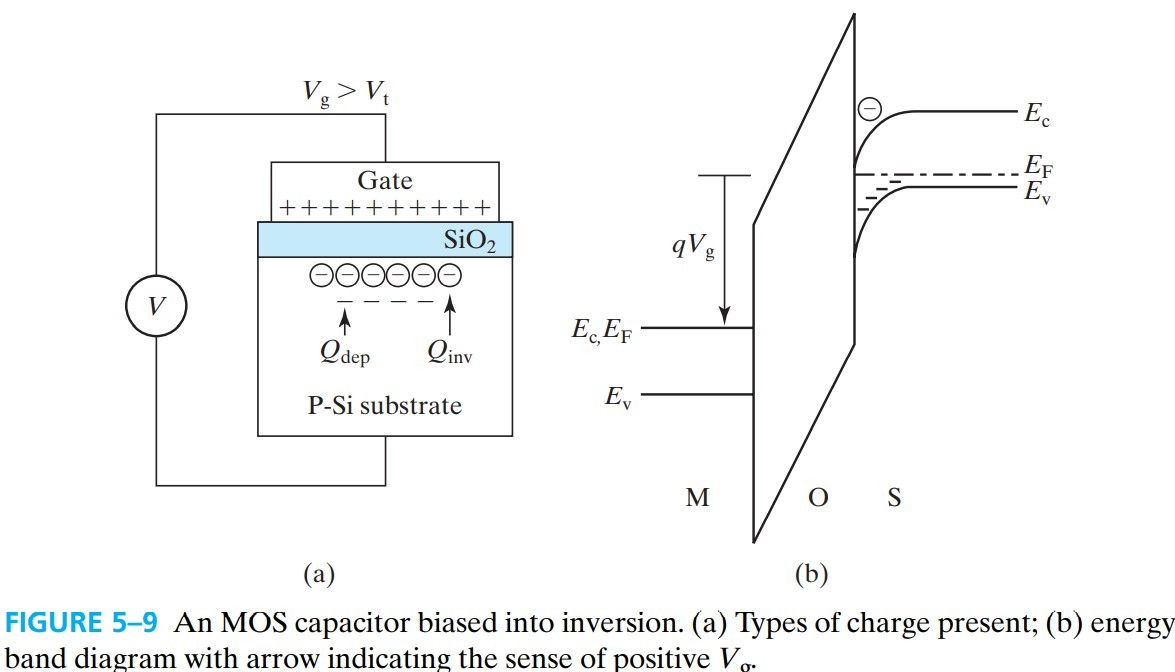
但与我们预想的不同,此时能带不会进一步弯曲,$\phi_s$ 维持在最大值 $2\phi_B$($\phi_B$ 是 $E_F$ 与 $E_i$ 的距离,见 fig 5-7),耗尽层也达到最大值:
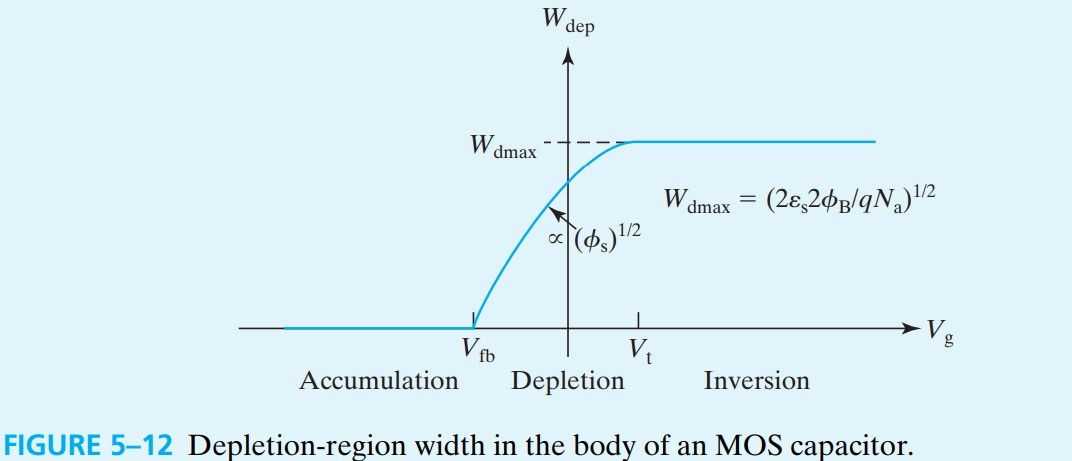
\[W_\text{dep} = \sqrt{\dfrac{2 \varepsilon_s \phi_s}{qN_a}}\\ \Rightarrow W_\text{dmax} = \sqrt{\dfrac{2 \varepsilon_s 2 \phi_B}{qN_a}} \tag{5.5.1}\]那能带不进一步弯曲,电子又是从哪来的呢?答案是,电子来自于 MOS transistor 两端的 ${\rm N^+}$(见fig 5-10a)(或者可以通过 thermal generation)。有了这些电子,我们可以把表面看作是 N-type layer
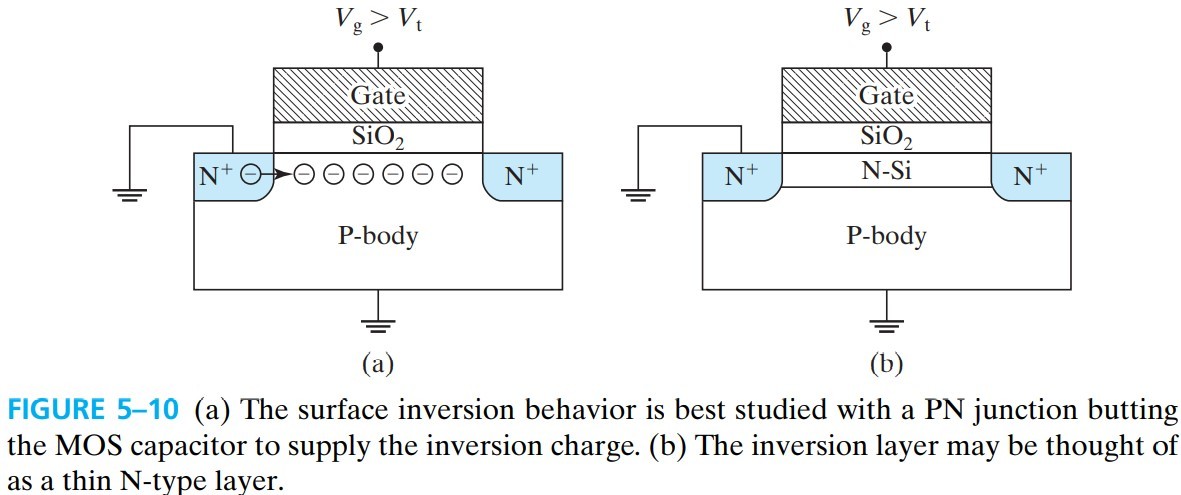
既然衬底能带不进一步弯曲,那多出来的电压就只能降在中间,所以($Q_\text{inv}<0$):
\[\begin{aligned} V_g &= V_\text{fb}+2\phi_B-\frac{Q_\text{dep}}{C_\text{ox}}\\ &=V_\text{fb}+2\phi_B+\frac{\sqrt{q N_a 2 \varepsilon+s 2 \phi_B}}{C_\text{ox}}-\frac{Q_\text{inv}}{C_\text{ox}}\\ &=V_t-\frac{Q_\text{inv}}{C_\text{ox}} \end{aligned} \tag{5.5.2}\]综上,我们有:
\[Q_\text{inv} = - C_\text{ox}(V_g-V_t) \tag{5.5.3}\]说明在 strong inversion 时,MOS behaves like a capacitor except for a voltage offset of $V_t$
5.5.1 Choice of Vt and Gate Doping Type
MOS 一般都是工作在 $V_t$ 附近,所以我们希望这个电压最好小点,因此,p衬底要用 ${\rm P^+}$ gate,n衬底要用 ${\rm N^+}$ gate.(书上并没有进一步解释)
另外,有个概念要记一下:A transistor that does not conduct current at $V_g = 0$ is called an enhancement-type device.
小结
上面我们考虑了 $V_g$ 从负到正的情况,依次称为:
- surface accumulation $V_g<V_\text{fb}$
- flat-Band condtion $V_g=V_\text{fb}$
- surface depletion $V_\text{fb}<V_g<V_t$
- threshold of inversion $V_g=V_t$
- strong inversion $V_g>V_t$
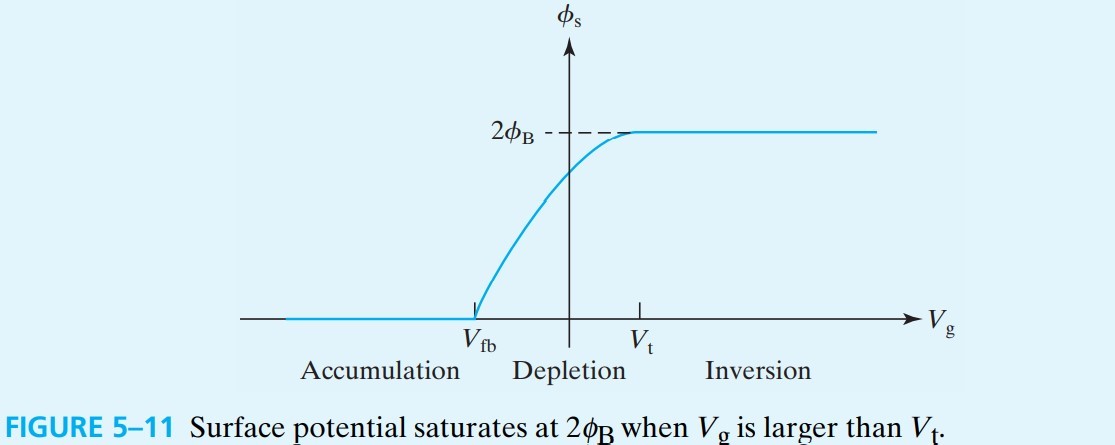
$\phi_s$ 的变化情况见上图,$W_\text{dep}$,$Q_\text{acc},Q_\text{dep},Q_\text{inv}$ 的变化情况见下图:
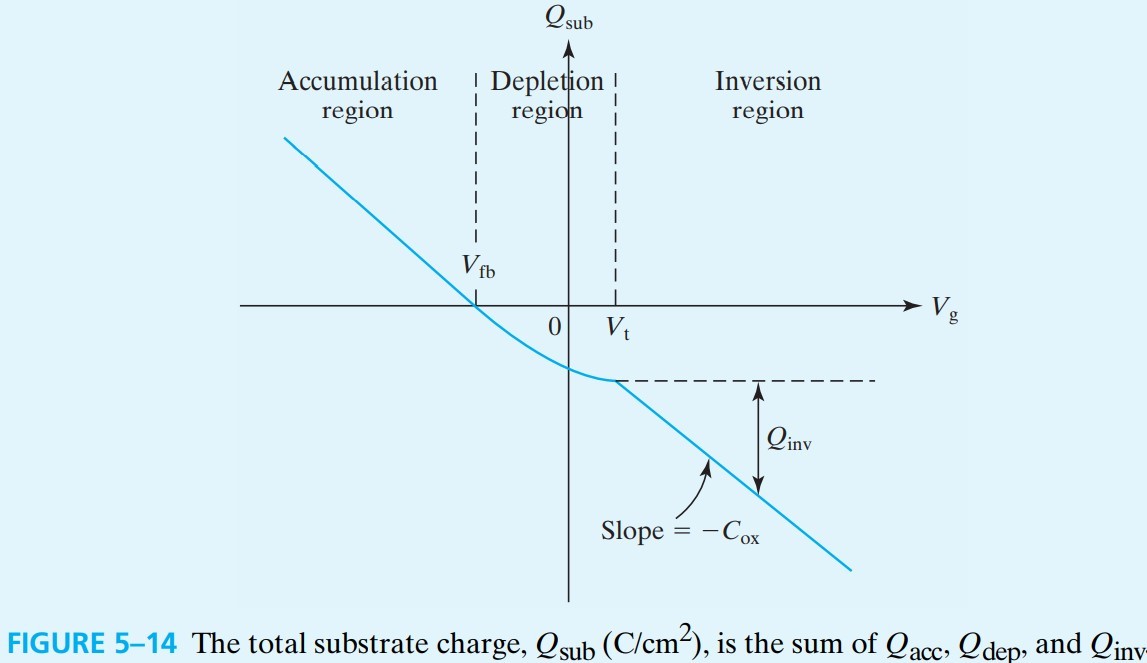
注意到在 Accumulation 和 Inversion region 均可以把 mos 看作电容。
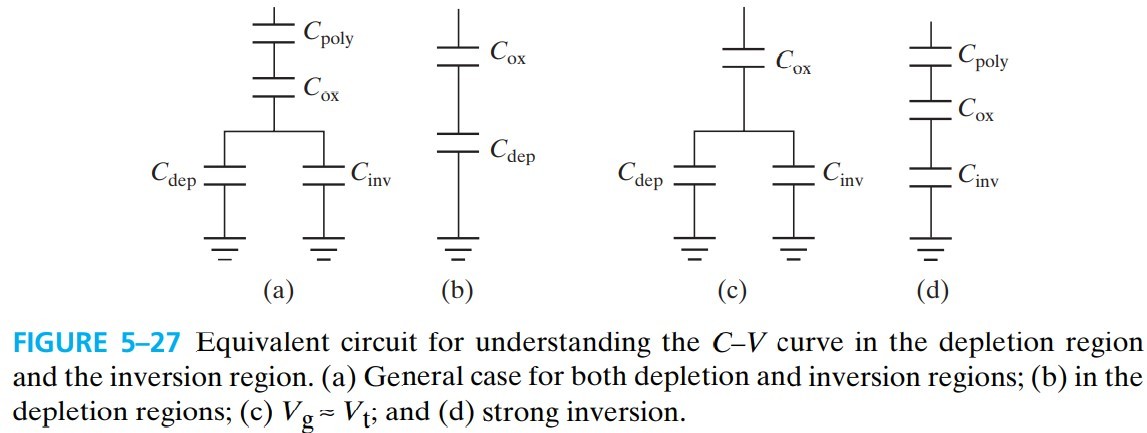
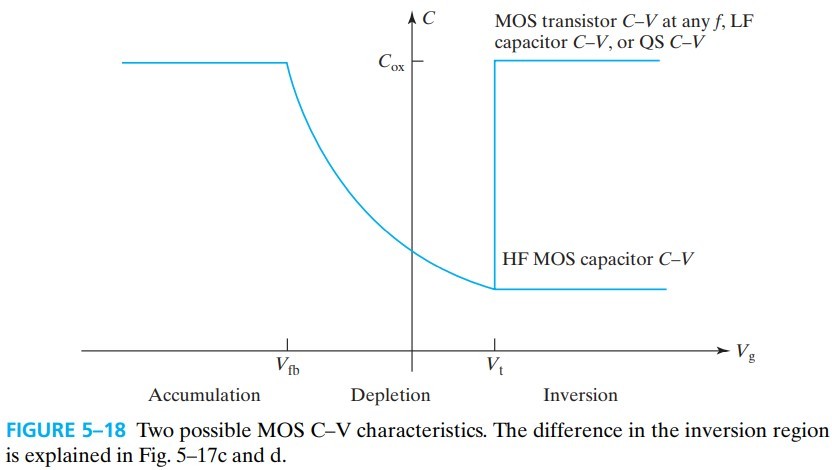
5.6 MOS C-V Characteristics
通过测量 capacitance–voltage 可得到 gate oxide thickness, substrate doping concentration, threshold voltage, and flat-band voltage. 测量方法是在一定 DC 直流偏压下,加以一个交流小信号 $V_g$(1 kHz–10 MHz),然后测量交流电流,从而 $i_\text{ac}/v_\text{ac}=\omega C$
上面的 MOS theory 中的电容指的是 small-signal capacitance
\[C \equiv \frac{\dif Q_g}{\dif V_g} = -\frac{\dif Q_\text{sub}}{\dif V_g} \tag{5.6.1}\]之所有有个负号,是因为 $V_g$ 和 $Q_\text{sub}$ 不是在同一片的极板上,所以要加负号。通过对 fig 5-14 求导,可以得到 fig 5-16 中的 quasi-static C–V 曲线:
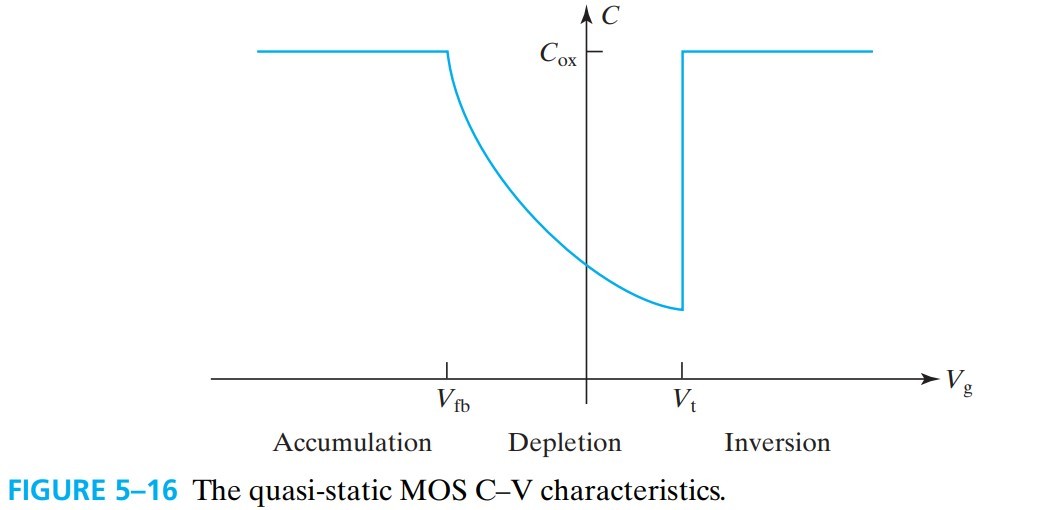
左边第一段是 $C_\text{ox}$(对应下图 a);中间是 $C_\text{ox}$ 与 $C_\text{dep}$ 串联,由于 $W_\text{dep}$ 的厚度会变化,所以电容也会变化(对应下图 b);最后 $W_\text{dep}$ 达到最大值,在 ${\rm Si-SiO_2}$ 有反型层电荷(由 ${\rm N^+}$ 提供),只有 $C_\text{ox}$(对应下图 c)
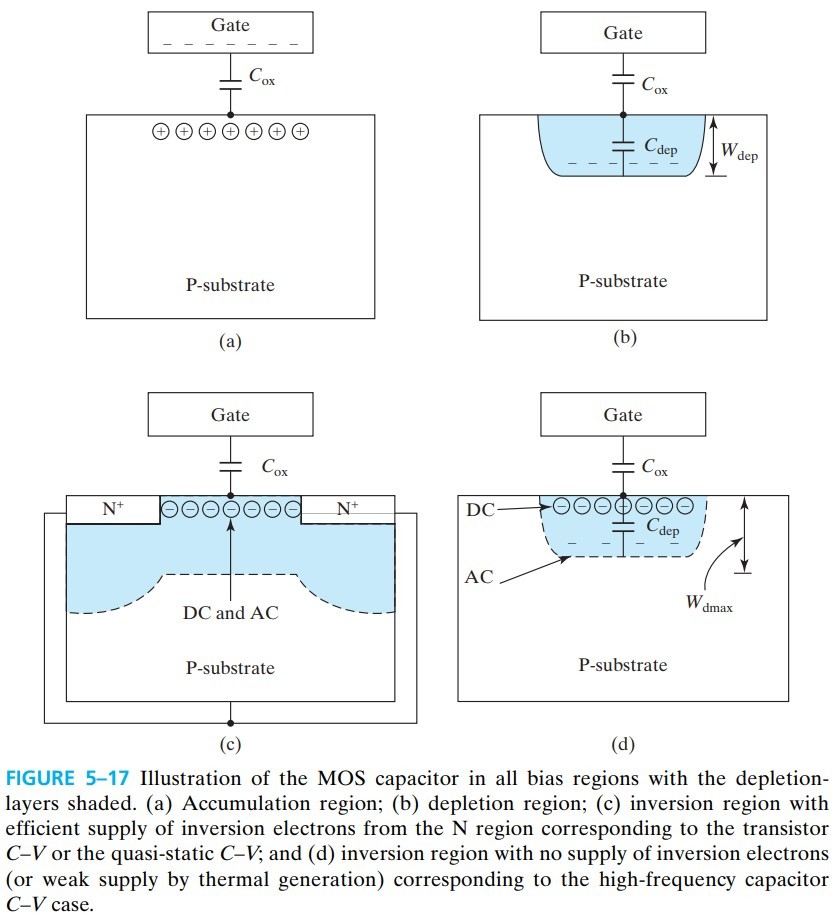
电容的准确公式如下:
\[C_\text{dep}=\frac{\varepsilon_s}{W_\text{dep}} \tag{5.6.2}\] \[\frac{1}{C}=\frac{1}{C_\text{ox}}+\frac{1}{C_\text{dep}} \tag{5.6.3}\]根据公式 $(5.3.3)$:
\[\begin{aligned} V_g &= V_\text{fb}+ \frac{q N_a W_\text{dep}^2}{2 \varepsilon_s}+\frac{q N_a W_\text{dep}}{C_\text{ox}}\\ &\Rightarrow \frac{2(V_g-V_\text{fb})}{q N_a \varepsilon_s}=\frac{1}{C_\text{dep}^2}+\frac{2}{C_\text{ox} C_\text{dep}} \\ &\Rightarrow \frac{2(V_g-V_\text{fb})}{q N_a \varepsilon_s}+\frac{1}{C_\text{ox}^2}=(\frac{1}{C_\text{dep}}+\frac{1}{C_\text{ox}})^2\\ &\Rightarrow \frac{1}{C}=\sqrt{\frac{2(V_g-V_\text{fb})}{q N_a \varepsilon_s}+\frac{1}{C_\text{ox}^2}} \end{aligned}\]从上式中可以看出,当 $V_g>V_\text{fb}$ 时,$W_\text{dep}$ expands,$C$ 减小。
我们上面讨论的是 quasi-static C–V,之所以叫 quasi-static,是因为我们认为 $Q_\text{inv}$ 可以迅速响应 AC(也就是AC的变化速度要慢于 $Q_\text{inc}$ 从 ${\rm N^+}$ 进入反型层的速度)。
如果 AC 变化的速度很快,导致 $Q_\text{inv}$ 来不及从 ${\rm N^+}$ 进来,那么就相当于 fig 5-17d 中的情况(没有了 ${\rm N^+}$)。$Q_\text{inv}$ 不变,同时 $\phi_s=2\phi_B$ 不变,$W_\text{dep}=W_\text{dmax}$ 也不变,所以 $C$ 只能维持在最低点。这样就得到 high-frequency MOS capacitor C–V
5.7 Oxide Charge - A Modification
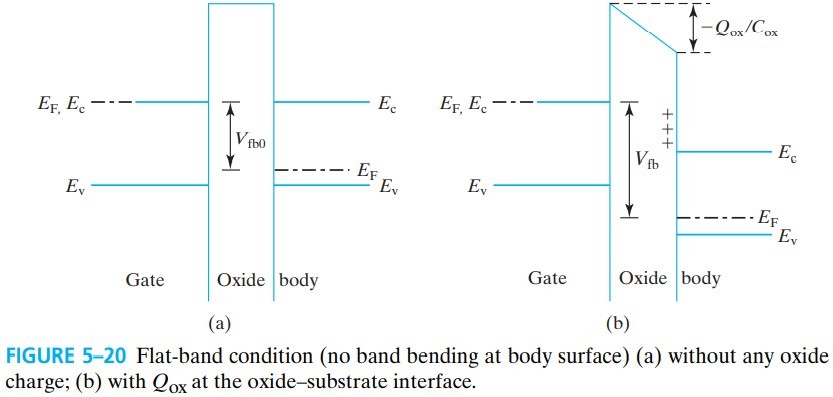
下面对 $V_\text{fv}$ 和 $V_t$ 的值进行一个修正。我们考虑 ${\rm SiO_2-Si}$ 表面电荷造成的电场对氧化层能带的影响,所以公式 $(5.1.1)$ 要修改为:
\[\begin{aligned} V_\text{fb}&=\psi_g-\psi_s-Q_\text{ox}/C_\text{ox}\\ &=\psi_g-\psi_s-Q_\text{ox}T_\text{ox}/\varepsilon_\text{ox} \end{aligned}\]根据式 $(5.4.3)$,$V_\text{fb}$ 会影响 $V_t$.
表面电荷并不是由电场导致的,而是本身就存在的。由很多种 oxide charge,比如:mobile oxide charge,sodium contamination, interface traps(interface states)
5.8 Poly-Si Gate Depletion
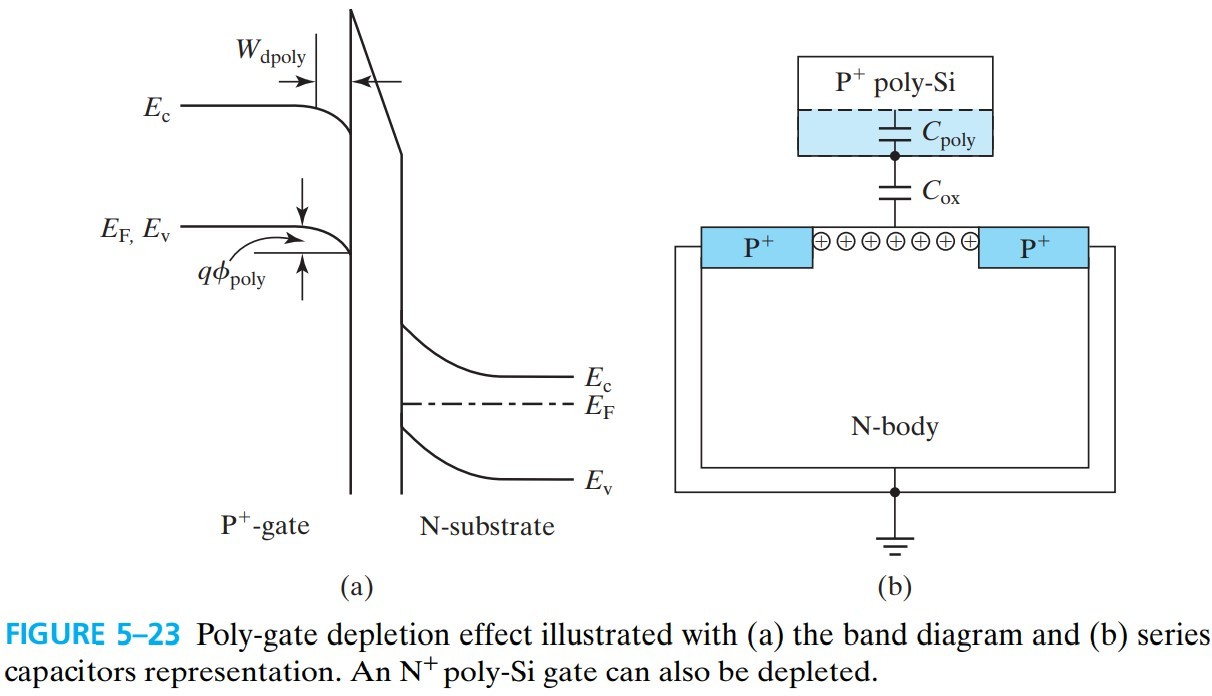
gate 的能带存在弯曲,如图 fig 5-23,产生的 poly-Si gate depletion 的厚度为:
\[W_\text{dpoly}=\varepsilon_\text{ox} \mathscr{E}_\text{ox}/qN_\text{poly}\]我们一般把 $C_\text{ox}$ 和 $C_\text{poly}$ 合在一起考虑:
\[\begin{aligned} C &= \left( \frac{1}{C_\text{ox}}+\frac{1}{C_\text{poly}} \right)^{-1}\\ &= \left( \frac{T_\text{ox}}{\varepsilon_\text{ox}}+\frac{W_\text{dpoly}}{\varepsilon_s} \right)^{-1}\\ &= \frac{\varepsilon_\text{ox}}{T_\text{ox}+W_\text{dpoly}\varepsilon_\text{ox}/\varepsilon_s}\\ &= \frac{\varepsilon_\text{ox}}{T_\text{ox}+W_\text{dpoly}/3} \end{aligned} \tag{5.8.2}\]从上式来看,相当于 $T_\text{ox}$ 增加到 $T_\text{ox}+W_\text{dpoly}/3$,这种效应称为 poly-depletion effect
这种效应会导致 $C$ 减小,导致 $Q_\text{inv}$ 减小,减小 transistor current. 我们可以用下面这公式来衡量 poly-gate depletion 对 $Q_\text{inv}$ 的影响:
\[Q_\text{inv} = -C_\text{ox} (V_g-\phi_\text{poly}-V_t)\\ W_\text{dpoly}=\sqrt{\frac{2\varepsilon_s \phi_\text{poly}}{q N_\text{poly}}}\]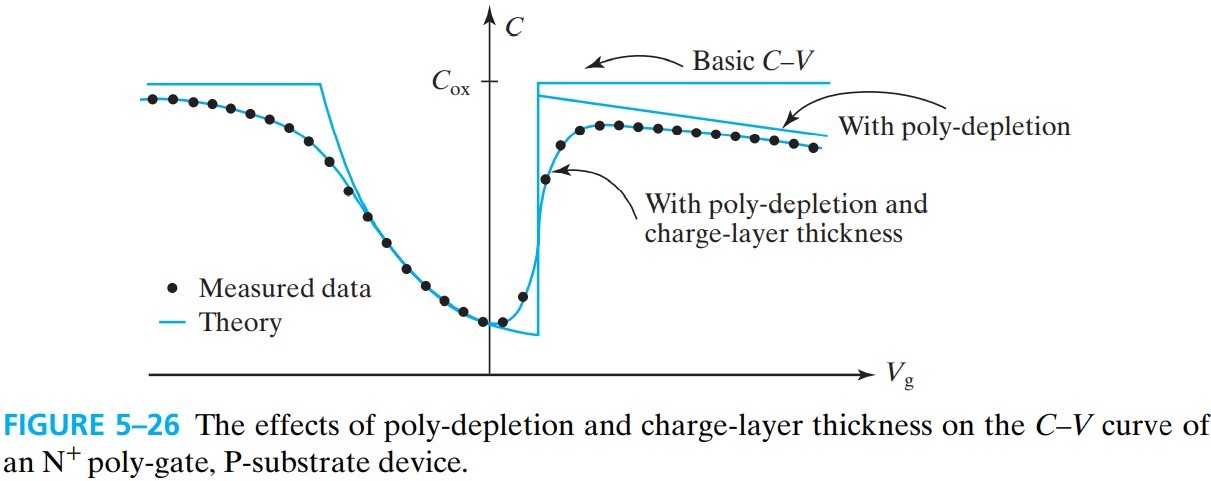
要减小这种效应,有几种方式:
- dope the poly-Si heavily
- 坏处:导致杂质渗入 oxide
- substitute the poly-gate with a metal gate(MOSFET)
5.9 Charge-Layer Thicknesses and Quantum Mechanical Effect
前面我们把反型层电荷看作集中在 ${\rm Si-SiO_2}$ 表面,但实际上这部分电荷是有一定厚度的,我们可以通过 Schrödinger equation and Poisson’s equation 解出来,所以我们将这个称为 quantum mechanical effect
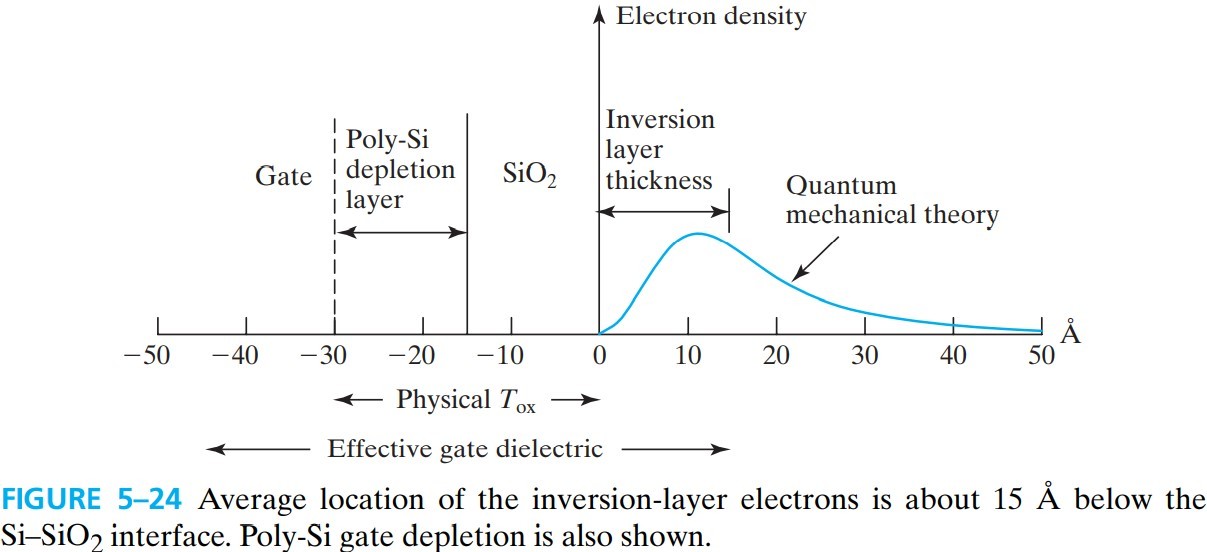
电荷分布的平均厚度为 inversion-layer thickness,$T_\text{inv}$,它和 gate depletion layer 一样对 $C$ 有影响,我们可以用 $(5.8.2)$ 类似的方法得到:
\[T_\text{oxe}=T_\text{ox}+W_\text{dpoly}/3+T_\text{inv}/3 \tag{5.9.2}\]$T_\text{oxe}$ 称为 electrical oxide thickness,可认为是 total effective oxide thickness,对应的电容称为 effective gate capacitance $C_\text{oxe}$,关系式如下:
\[\begin{aligned} Q_\text{inv}&=-C_\text{oxe}(V_g-V_t)\\ &=\frac{\varepsilon_\text{ox}}{T_\text{oxe}}(V_g-V_t) \end{aligned} \tag{5.9.3}\]对上面各个电容的总结见下图: