本节需要的函数
点击展开
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
import numpy as np
def identity_function(x):
return x
def step_function(x):
return np.array(x > 0, dtype=np.int)
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def sigmoid_grad(x):
return (1.0 - sigmoid(x)) * sigmoid(x)
def relu(x):
return np.maximum(0, x)
def relu_grad(x):
grad = np.zeros(x)
grad[x>=0] = 1
return grad
def softmax(x):
if x.ndim == 2:
x = x.T
x = x - np.max(x, axis=0)
y = np.exp(x) / np.sum(np.exp(x), axis=0)
return y.T
x = x - np.max(x) # 溢出对策
return np.exp(x) / np.sum(np.exp(x))
def mean_squared_error(y, t):
return 0.5 * np.sum((y-t)**2)
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
# 监督数据是one-hot-vector的情况下,转换为正确解标签的索引
if t.size == y.size:
t = t.argmax(axis=1)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size
def softmax_loss(X, t):
y = softmax(X)
return cross_entropy_error(y, t)
def numerical_gradient(f, x):
h = 1e-4 # 0.0001
grad = np.zeros_like(x)
it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
while not it.finished:
idx = it.multi_index
tmp_val = x[idx]
x[idx] = float(tmp_val) + h
fxh1 = f(x) # f(x+h)
x[idx] = tmp_val - h
fxh2 = f(x) # f(x-h)
grad[idx] = (fxh1 - fxh2) / (2*h)
x[idx] = tmp_val # 还原值
it.iternext()
return grad
神经网络的学习
上一节也看到了,随机生成的参数要是能有高准确率那就有鬼了。当然,几千个参数靠人来设置也不现实。所以需要靠计算机来自动调整:
- 对于一般的机器学习,机器会根据样本的“特征”来调整参数,而特征是由人来设置的。
- 对于神经网络,我们直接将整个样本输入到网络,无需设置任何特征。
因此神经网络的应用范围更广。
训练数据与测试数据
训练数据用于训练神经网络,寻找最优参数。
测试数据用来测试神经网络。
为什么要这样划分?因为如果只用训练数据来测试,那么很有可能神经网络只能识别训练数据,而无法识别其他数据。就好像做题,如果只做一类题,那就有可能在考试时做不出新的类型的题目了。这种做考试题的能力,在深度学习中叫 泛化;而只会做一类题叫 过拟合。
损失函数
我们用 损失函数 loss function 来衡量神经网络的误差。
均方误差
最简单的损失函数就是均方误差:
\[E = \frac{1}{2} \sum_k (y_k - t_k)^2\]import numpy as np
def mean_squared_error(y, t):
return 0.5 * np.sum((y-t)**2)
y1 = np.array([0.1,0.7,0.2])
y2 = np.array([0.1,0.5,0.4])
t = np.array([0,1,0])
[mean_squared_error(t,t),
mean_squared_error(y1,t),
mean_squared_error(y2,t)]
OUTPUT
[0.0, 0.07000000000000002, 0.21000000000000002]
交叉熵误差
\[E=-\sum_k t_k \log y_k\]输出的值只取决于正确标签对应的输出。如果输出是 $y=1$,则 $E=0$;如果输出 $y<1$,则 $E>0$。
batch 学习的交叉熵误差:
\[E=-\frac{1}{N} \sum_n \sum_k t_{n,k} \log y_{n,k}\]相当是所有训练数据的误差平均值。
import numpy as np
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
# 监督数据是one-hot-vector的情况下,转换为正确解标签的索引
if t.size == y.size:
t = t.argmax(axis=1)
batch_size = y.shape[0]
#加上微小值防止出现负无穷
return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size
y1 = np.array([0.1,0.7,0.2])
y2 = np.array([0.1,0.5,0.4])
t = np.array([0,1,0])
[cross_entropy_error(t,t),
cross_entropy_error(y1,t),
cross_entropy_error(y2,t)]
OUTPUT
[-9.999999505838704e-08, 0.3566748010815999, 0.6931469805599654]
能不能用准确率来作为损失函数
显然是不能的。准确率指的是有多少个是正确的,比如100个数据中有32个正确,那精度就是32%。显然,准确率是不连续的,或者说是突变的,这样我们如果微调参数,那么准确率是不会变化的,这样就无法确定应该向哪个方向调整参数。这和阶跃函数无法作为激活函数的理由是一样的。
梯度
假如神经网络可以写成一个函数 $y=f(w, x)$ ,误差函数为 $L(f(w, x))$ ,为了使函数更准确,也就是误差函数最小。那么根据梯度的定义,我们可以向梯度方向减小参数:
\[w_0' = w_0 - \eta\frac{\partial L(f(x,w))}{\partial w_0}\]$\eta$ 称为学习率
下面我们来看看如何求网络的梯度:
def numerical_gradient(f, x): #笨方法求梯度
h = 1e-4 # 0.0001
grad = np.zeros_like(x)
it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
while not it.finished:
idx = it.multi_index
tmp_val = x[idx]
x[idx] = float(tmp_val) + h
fxh1 = f(x) # f(x+h)
x[idx] = tmp_val - h
fxh2 = f(x) # f(x-h)
grad[idx] = (fxh1 - fxh2) / (2*h) #取相近两点求斜率
x[idx] = tmp_val # 还原值
it.iternext()
return grad
import numpy as np
class simpleNet:
def __init__(self):
self.W = np.random.randn(2,3) #随机生成参数
def predict(self, x): #预测
return np.dot(x, self.W)
def loss(self, x, t): #计算误差
z = self.predict(x)
y = softmax(z)
loss = cross_entropy_error(y, t)
return loss
x = np.array([0.6, 0.9])
t = np.array([0, 0, 1])
net = simpleNet()
f = lambda w: net.loss(x, t)
dW = numerical_gradient(f, net.W)
print(net.loss(x,t))
print(dW)
OUTPUT
0.2698596081175344
[[ 0.11629091 0.02561713 -0.14190804]
[ 0.17443636 0.03842569 -0.21286206]]
求完梯度后更新梯度:
eta = 1
print(net.W)
print(net.loss(x,t))
for i in range(10): #利用梯度下降法更新十次参数
net.W = net.W - eta*numerical_gradient(f, net.W)
print(net.W)
print(net.loss(x,t))
OUTPUT
[[-0.52760346 -0.60826468 0.14784348]
[-0.53011149 -2.15726367 0.54289599]]
0.2698596081175344
[[-0.98917483 -0.74641069 0.74756086]
[-1.22246854 -2.36448269 1.44247207]]
0.044317052837686284
可以看出,训练 10 次后,误差已经减小了 2 个数量级。这就是我们希望达到的目标
回到MNIST数据集
我们尝试用一个两层的网络来识别 MNIST 数据集,我们将定义一个 TwoLayerNet,并实现相关的函数(预测、损失函数、精度、梯度……)
TwoLayerNet
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
class TwoLayerNet: #一个简单的两层网路
def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
# 初始化权重
self.params = {}
self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size) #权重
self.params['b1'] = np.zeros(hidden_size) #偏置
self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
self.params['b2'] = np.zeros(output_size)
def predict(self, x):
W1, W2 = self.params['W1'], self.params['W2']
b1, b2 = self.params['b1'], self.params['b2']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
y = softmax(a2)
return y
# x:输入数据, t:监督数据
def loss(self, x, t):
y = self.predict(x)
return cross_entropy_error(y, t)
def accuracy(self, x, t):
y = self.predict(x)
y = np.argmax(y, axis=1)
t = np.argmax(t, axis=1)
accuracy = np.sum(y == t) / float(x.shape[0])
return accuracy
# x:输入数据, t:监督数据
def numerical_gradient(self, x, t):
loss_W = lambda W: self.loss(x, t)
grads = {}
grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
return grads
def gradient(self, x, t):
W1, W2 = self.params['W1'], self.params['W2']
b1, b2 = self.params['b1'], self.params['b2']
grads = {}
batch_num = x.shape[0]
# forward
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
y = softmax(a2)
# backward
dy = (y - t) / batch_num
grads['W2'] = np.dot(z1.T, dy)
grads['b2'] = np.sum(dy, axis=0)
da1 = np.dot(dy, W2.T)
dz1 = sigmoid_grad(a1) * da1
grads['W1'] = np.dot(x.T, dz1)
grads['b1'] = np.sum(dz1, axis=0)
return grads
Load MNIST
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
try:
import urllib.request
except ImportError:
raise ImportError('You should use Python 3.x')
import os.path
from IPython.terminal.embed import InteractiveShellEmbed
import gzip
import pickle
import os
import numpy as np
url_base = 'http://yann.lecun.com/exdb/mnist/'
key_file = {
'train_img':'train-images-idx3-ubyte.gz',
'train_label':'train-labels-idx1-ubyte.gz',
'test_img':'t10k-images-idx3-ubyte.gz',
'test_label':'t10k-labels-idx1-ubyte.gz'
}
## if you run in terminal, run this
# dataset_dir = os.path.dirname(os.path.abspath(__file__))
## if you run in IPython, run this
ip_shell = InteractiveShellEmbed()
dataset_dir = ip_shell.magic("%pwd")
save_file = dataset_dir + "/mnist.pkl"
train_num = 60000
test_num = 10000
img_dim = (1, 28, 28)
img_size = 784
def _download(file_name):
file_path = dataset_dir + "/" + file_name
if os.path.exists(file_path):
return
print("Downloading " + file_name + " ... ")
urllib.request.urlretrieve(url_base + file_name, file_path)
print("Done")
def download_mnist():
for v in key_file.values():
_download(v)
def _load_label(file_name):
file_path = dataset_dir + "/" + file_name
print("Converting " + file_name + " to NumPy Array ...")
with gzip.open(file_path, 'rb') as f:
labels = np.frombuffer(f.read(), np.uint8, offset=8)
print("Done")
return labels
def _load_img(file_name):
file_path = dataset_dir + "/" + file_name
print("Converting " + file_name + " to NumPy Array ...")
with gzip.open(file_path, 'rb') as f:
data = np.frombuffer(f.read(), np.uint8, offset=16)
data = data.reshape(-1, img_size)
print("Done")
return data
def _convert_numpy():
dataset = {}
dataset['train_img'] = _load_img(key_file['train_img'])
dataset['train_label'] = _load_label(key_file['train_label'])
dataset['test_img'] = _load_img(key_file['test_img'])
dataset['test_label'] = _load_label(key_file['test_label'])
return dataset
def init_mnist():
download_mnist()
dataset = _convert_numpy()
print("Creating pickle file ...")
with open(save_file, 'wb') as f:
pickle.dump(dataset, f, -1)
print("Done!")
def _change_one_hot_label(X):
T = np.zeros((X.size, 10))
for idx, row in enumerate(T):
row[X[idx]] = 1
return T
def load_mnist(normalize=True, flatten=True, one_hot_label=False):
"""读入MNIST数据集
Parameters
----------
normalize : 将图像的像素值正规化为0.0~1.0
one_hot_label :
one_hot_label为True的情况下,标签作为one-hot数组返回
one-hot数组是指[0,0,1,0,0,0,0,0,0,0]这样的数组
flatten : 是否将图像展开为一维数组
Returns
-------
(训练图像, 训练标签), (测试图像, 测试标签)
"""
if not os.path.exists(save_file):
init_mnist()
with open(save_file, 'rb') as f:
dataset = pickle.load(f)
if normalize:
for key in ('train_img', 'test_img'):
dataset[key] = dataset[key].astype(np.float32)
dataset[key] /= 255.0
if one_hot_label:
dataset['train_label'] = _change_one_hot_label(dataset['train_label'])
dataset['test_label'] = _change_one_hot_label(dataset['test_label'])
if not flatten:
for key in ('train_img', 'test_img'):
dataset[key] = dataset[key].reshape(-1, 1, 28, 28)
return (dataset['train_img'], dataset['train_label']), (dataset['test_img'], dataset['test_label'])
if __name__ == '__main__':
init_mnist()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
OUTPUT:
Downloading train-images-idx3-ubyte.gz ...
Done
Downloading train-labels-idx1-ubyte.gz ...
Done
Downloading t10k-images-idx3-ubyte.gz ...
Done
Downloading t10k-labels-idx1-ubyte.gz ...
Done
Converting train-images-idx3-ubyte.gz to NumPy Array ...
Done
Converting train-labels-idx1-ubyte.gz to NumPy Array ...
Done
Converting t10k-images-idx3-ubyte.gz to NumPy Array ...
Done
Converting t10k-labels-idx1-ubyte.gz to NumPy Array ...
Done
Creating pickle file ...
Done!
Training
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
import numpy as np
import matplotlib.pyplot as plt
# 读入数据
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)
iters_num = 10000 # 适当设定循环的次数
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1
train_loss_list = []
train_acc_list = []
test_acc_list = []
iter_per_epoch = max(train_size / batch_size, 1)
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
# 计算梯度
#grad = network.numerical_gradient(x_batch, t_batch)
grad = network.gradient(x_batch, t_batch)
# 更新参数
for key in ('W1', 'b1', 'W2', 'b2'):
network.params[key] -= learning_rate * grad[key]
loss = network.loss(x_batch, t_batch)
train_loss_list.append(loss)
if i % iter_per_epoch == 0:
train_acc = network.accuracy(x_train, t_train)
test_acc = network.accuracy(x_test, t_test)
train_acc_list.append(train_acc)
test_acc_list.append(test_acc)
print("train acc, test acc | " + str(train_acc) + ", " + str(test_acc))
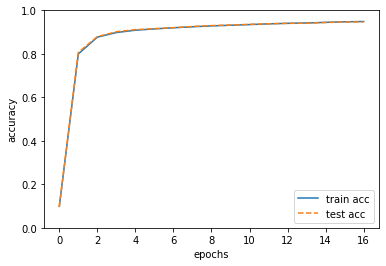
# 绘制图形
markers = {'train': 'o', 'test': 's'}
x = np.arange(len(train_acc_list))
plt.plot(x, train_acc_list, label='train acc')
plt.plot(x, test_acc_list, label='test acc', linestyle='--')
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
plt.show()
OUTPUT
train acc, test acc | 0.09863333333333334, 0.0958
train acc, test acc | 0.7995166666666667, 0.8065
train acc, test acc | 0.8767, 0.8792
train acc, test acc | 0.898, 0.9016
train acc, test acc | 0.9086333333333333, 0.9114
train acc, test acc | 0.9147666666666666, 0.9157
train acc, test acc | 0.91985, 0.9204
train acc, test acc | 0.9245, 0.9257
train acc, test acc | 0.9285666666666667, 0.93
train acc, test acc | 0.9315, 0.9325
train acc, test acc | 0.93455, 0.9357
train acc, test acc | 0.9379166666666666, 0.9383
train acc, test acc | 0.94035, 0.9403
train acc, test acc | 0.9420166666666666, 0.9408
train acc, test acc | 0.9448666666666666, 0.9442
train acc, test acc | 0.9472833333333334, 0.9468
train acc, test acc | 0.9488166666666666, 0.947