本节需要的函数
基本函数(阶跃、gimomid等)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
import numpy as np
def identity_function(x):
return x
def step_function(x):
return np.array(x > 0, dtype=np.int)
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def sigmoid_grad(x):
return (1.0 - sigmoid(x)) * sigmoid(x)
def relu(x):
return np.maximum(0, x)
def relu_grad(x):
grad = np.zeros(x)
grad[x>=0] = 1
return grad
def softmax(x):
if x.ndim == 2:
x = x.T
x = x - np.max(x, axis=0)
y = np.exp(x) / np.sum(np.exp(x), axis=0)
return y.T
x = x - np.max(x) # 溢出对策
return np.exp(x) / np.sum(np.exp(x))
def mean_squared_error(y, t):
return 0.5 * np.sum((y-t)**2)
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
# 监督数据是one-hot-vector的情况下,转换为正确解标签的索引
if t.size == y.size:
t = t.argmax(axis=1)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size
def softmax_loss(X, t):
y = softmax(X)
return cross_entropy_error(y, t)
def numerical_gradient(f, x):
h = 1e-4 # 0.0001
grad = np.zeros_like(x)
it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
while not it.finished:
idx = it.multi_index
tmp_val = x[idx]
x[idx] = float(tmp_val) + h
fxh1 = f(x) # f(x+h)
x[idx] = tmp_val - h
fxh2 = f(x) # f(x-h)
grad[idx] = (fxh1 - fxh2) / (2*h)
x[idx] = tmp_val # 还原值
it.iternext()
return grad
计算图的基本函数(Relu、Sigmoid等)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
class Relu:
def __init__(self):
self.mask = None
def forward(self, x):
self.mask = (x <= 0)
out = x.copy()
out[self.mask] = 0
return out
def backward(self, dout):
dout[self.mask] = 0
dx = dout
return dx
class Sigmoid:
def __init__(self):
self.out = None
def forward(self, x):
out = sigmoid(x)
self.out = out
return out
def backward(self, dout):
dx = dout * (1.0 - self.out) * self.out
return dx
class Affine:
def __init__(self, W, b):
self.W =W
self.b = b
self.x = None
self.original_x_shape = None
# 权重和偏置参数的导数
self.dW = None
self.db = None
def forward(self, x):
# 对应张量
self.original_x_shape = x.shape
x = x.reshape(x.shape[0], -1)
self.x = x
out = np.dot(self.x, self.W) + self.b
return out
def backward(self, dout):
dx = np.dot(dout, self.W.T)
self.dW = np.dot(self.x.T, dout)
self.db = np.sum(dout, axis=0)
dx = dx.reshape(*self.original_x_shape) # 还原输入数据的形状(对应张量)
return dx
class SoftmaxWithLoss:
def __init__(self):
self.loss = None
self.y = None # softmax的输出
self.t = None # 监督数据
def forward(self, x, t):
self.t = t
self.y = softmax(x)
self.loss = cross_entropy_error(self.y, self.t)
return self.loss
def backward(self, dout=1):
batch_size = self.t.shape[0]
if self.t.size == self.y.size: # 监督数据是one-hot-vector的情况
dx = (self.y - self.t) / batch_size
else:
dx = self.y.copy()
dx[np.arange(batch_size), self.t] -= 1
dx = dx / batch_size
return dx
数值微分求梯度
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
def _numerical_gradient_1d(f, x):
h = 1e-4 # 0.0001
grad = np.zeros_like(x)
for idx in range(x.size):
tmp_val = x[idx]
x[idx] = float(tmp_val) + h
fxh1 = f(x) # f(x+h)
x[idx] = tmp_val - h
fxh2 = f(x) # f(x-h)
grad[idx] = (fxh1 - fxh2) / (2*h)
x[idx] = tmp_val # 还原值
return grad
def numerical_gradient_2d(f, X):
if X.ndim == 1:
return _numerical_gradient_1d(f, X)
else:
grad = np.zeros_like(X)
for idx, x in enumerate(X):
grad[idx] = _numerical_gradient_1d(f, x)
return grad
def numerical_gradient(f, x):
h = 1e-4 # 0.0001
grad = np.zeros_like(x)
it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
while not it.finished:
idx = it.multi_index
tmp_val = x[idx]
x[idx] = float(tmp_val) + h
fxh1 = f(x) # f(x+h)
x[idx] = tmp_val - h
fxh2 = f(x) # f(x-h)
grad[idx] = (fxh1 - fxh2) / (2*h)
x[idx] = tmp_val # 还原值
it.iternext()
return grad
加载MNIST数据集
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
try:
import urllib.request
except ImportError:
raise ImportError('You should use Python 3.x')
import os.path
from IPython.terminal.embed import InteractiveShellEmbed
import gzip
import pickle
import os
import numpy as np
url_base = 'http://yann.lecun.com/exdb/mnist/'
key_file = {
'train_img':'train-images-idx3-ubyte.gz',
'train_label':'train-labels-idx1-ubyte.gz',
'test_img':'t10k-images-idx3-ubyte.gz',
'test_label':'t10k-labels-idx1-ubyte.gz'
}
## if you run in terminal, run this
# dataset_dir = os.path.dirname(os.path.abspath(__file__))
## if you run in IPython, run this
ip_shell = InteractiveShellEmbed()
dataset_dir = ip_shell.magic("%pwd")
save_file = dataset_dir + "/mnist.pkl"
train_num = 60000
test_num = 10000
img_dim = (1, 28, 28)
img_size = 784
def _download(file_name):
file_path = dataset_dir + "/" + file_name
if os.path.exists(file_path):
return
print("Downloading " + file_name + " ... ")
urllib.request.urlretrieve(url_base + file_name, file_path)
print("Done")
def download_mnist():
for v in key_file.values():
_download(v)
def _load_label(file_name):
file_path = dataset_dir + "/" + file_name
print("Converting " + file_name + " to NumPy Array ...")
with gzip.open(file_path, 'rb') as f:
labels = np.frombuffer(f.read(), np.uint8, offset=8)
print("Done")
return labels
def _load_img(file_name):
file_path = dataset_dir + "/" + file_name
print("Converting " + file_name + " to NumPy Array ...")
with gzip.open(file_path, 'rb') as f:
data = np.frombuffer(f.read(), np.uint8, offset=16)
data = data.reshape(-1, img_size)
print("Done")
return data
def _convert_numpy():
dataset = {}
dataset['train_img'] = _load_img(key_file['train_img'])
dataset['train_label'] = _load_label(key_file['train_label'])
dataset['test_img'] = _load_img(key_file['test_img'])
dataset['test_label'] = _load_label(key_file['test_label'])
return dataset
def init_mnist():
download_mnist()
dataset = _convert_numpy()
print("Creating pickle file ...")
with open(save_file, 'wb') as f:
pickle.dump(dataset, f, -1)
print("Done!")
def _change_one_hot_label(X):
T = np.zeros((X.size, 10))
for idx, row in enumerate(T):
row[X[idx]] = 1
return T
def load_mnist(normalize=True, flatten=True, one_hot_label=False):
"""读入MNIST数据集
Parameters
----------
normalize : 将图像的像素值正规化为0.0~1.0
one_hot_label :
one_hot_label为True的情况下,标签作为one-hot数组返回
one-hot数组是指[0,0,1,0,0,0,0,0,0,0]这样的数组
flatten : 是否将图像展开为一维数组
Returns
-------
(训练图像, 训练标签), (测试图像, 测试标签)
"""
if not os.path.exists(save_file):
init_mnist()
with open(save_file, 'rb') as f:
dataset = pickle.load(f)
if normalize:
for key in ('train_img', 'test_img'):
dataset[key] = dataset[key].astype(np.float32)
dataset[key] /= 255.0
if one_hot_label:
dataset['train_label'] = _change_one_hot_label(dataset['train_label'])
dataset['test_label'] = _change_one_hot_label(dataset['test_label'])
if not flatten:
for key in ('train_img', 'test_img'):
dataset[key] = dataset[key].reshape(-1, 1, 28, 28)
return (dataset['train_img'], dataset['train_label']), (dataset['test_img'], dataset['test_label'])
if __name__ == '__main__':
init_mnist()
使图形变圆滑
1
2
3
4
5
6
7
8
9
10
11
12
import numpy as np
def smooth_curve(x):
"""用于使损失函数的图形变圆滑
参考:http://glowingpython.blogspot.jp/2012/02/convolution-with-numpy.html
"""
window_len = 11
s = np.r_[x[window_len-1:0:-1], x, x[-1:-window_len:-1]]
w = np.kaiser(window_len, 2)
y = np.convolve(w/w.sum(), s, mode='valid')
return y[5:len(y)-5]
参数的更新
随机梯度下降 SGD
\[\newcommand{\bd}{\boldsymbol}\]深度学习的目的就是找到令损失函数最小的参数,找最优参数的过程称为 最优化(optimization)。前面的最优化使用的是梯度下降的方法,由于我们一开始的参数初始值是随机的,所以又称 随机梯度下降法(SGD,Stochastic Gradient Descent)。SGD用数学表示为:
\[\bd{W} \leftarrow \bd{W} - \eta \frac{\partial L}{\partial \bd{W}}\\ \bd{W}:权重 \quad \eta:学习率 \quad L:损失函数\]import numpy as np
class SGD:
"""随机梯度下降法(Stochastic Gradient Descent)"""
def __init__(self, lr=0.01):
self.lr = lr
def update(self, params, grads):
for key in params.keys():
params[key] -= self.lr * grads[key]
但SGD有个缺点。比如我们考虑求函数 $f(x,y)=\frac{1}{20} x^2 + y^2$ 的最小值,如下图所示:
import numpy as np
import matplotlib.pyplot as plt
def f(x, y):
return x**2 / 20.0 + y**2
x = np.linspace(-10,10,30)
y = np.linspace(-10,10,30)
X, Y = np.meshgrid(x, y)
Z = f(X,Y)
fig = plt.figure()
ax = plt.axes(projection='3d')
ax.contour3D(X, Y, Z, 50, cmap='binary')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
#调整观察角度和方位角。这里将俯仰角设为60度,把方位角调整为35度
ax.view_init(60, 35)
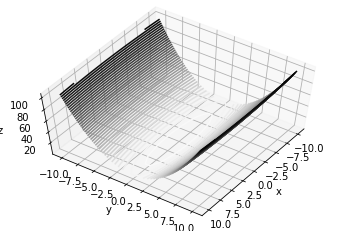
从图中可以看出,这个函数的梯度并不是均匀的,而是在y轴方向大,在x轴方向小。如果我们从边上的某个点出发,利用SGD去寻找最小值,那么我们就会发现寻找的过程是这样的:
SGD搜索最小值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
import numpy as np
import matplotlib.pyplot as plt
from collections import OrderedDict
def f(x, y):
return x**2 / 20.0 + y**2
def df(x, y):
return x / 10.0, 2.0*y
init_pos = (-7.0, 2.0)
params = {}
params['x'], params['y'] = init_pos[0], init_pos[1]
grads = {}
grads['x'], grads['y'] = 0, 0
optimizers = OrderedDict()
optimizers["SGD"] = SGD(lr=0.95)
#optimizers["Momentum"] = Momentum(lr=0.1)
#optimizers["AdaGrad"] = AdaGrad(lr=1.5)
#optimizers["Adam"] = Adam(lr=0.3)
idx = 1
for key in optimizers:
optimizer = optimizers[key]
x_history = []
y_history = []
params['x'], params['y'] = init_pos[0], init_pos[1]
for i in range(30):
x_history.append(params['x'])
y_history.append(params['y'])
grads['x'], grads['y'] = df(params['x'], params['y'])
optimizer.update(params, grads)
x = np.arange(-10, 10, 0.01)
y = np.arange(-5, 5, 0.01)
X, Y = np.meshgrid(x, y)
Z = f(X, Y)
# for simple contour line
mask = Z > 7
Z[mask] = 0
# plot
#plt.subplot(2, 2, idx)
#idx += 1
plt.figure(figsize=(5,5))
plt.plot(x_history, y_history, 'o-', color="red")
plt.contour(X, Y, Z)
plt.ylim(-10, 10)
plt.xlim(-10, 10)
plt.plot(0, 0, '+')
#colorbar()
#spring()
plt.title(key)
plt.xlabel("x")
plt.ylabel("y")
plt.show()
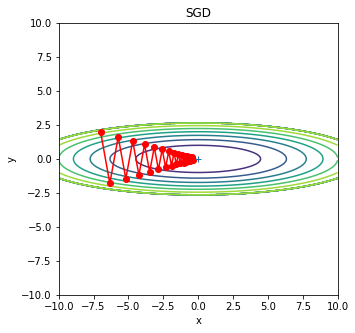
图中,SGD的路径呈“之”字形,非常低效。因此,如果函数的形状非均向(anisotropic),那么梯度的方向就不是指向最小值,搜索效率会很低。
Momentum SGD
Momentum 表示动量,其原理就和物理世界一样,想象有个小球从最高点滑到最低点,小球在下降的过程中,会带有一定动量,从而其轨迹并不是沿梯度下降的方向,而是在动量惯性的作用下接近最低点。
用数学方法表示如下:
\[\bd{v} \leftarrow \alpha \bd{v} -\eta \frac{\partial L}{\partial \bd{W}}\\ \bd{W} \leftarrow \bd{W} + \bd{v}\]这里引入的速度 $\bd{v}$,参数会向速度方向更新,同时,之前的动量也会影响速度,所以有 $\alpha \bd{v}$ 项,由于动量会因为摩擦力等因素而减小,所以 $\alpha<1$。
class Momentum:
"""Momentum SGD"""
def __init__(self, lr=0.01, momentum=0.9):
self.lr = lr
self.momentum = momentum
self.v = None
def update(self, params, grads):
if self.v is None:
self.v = {}
for key, val in params.items():
self.v[key] = np.zeros_like(val)
for key in params.keys():
self.v[key] = self.momentum*self.v[key] - self.lr*grads[key]
params[key] += self.v[key]
Momentum搜索最小值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
import numpy as np
import matplotlib.pyplot as plt
from collections import OrderedDict
def f(x, y):
return x**2 / 20.0 + y**2
def df(x, y):
return x / 10.0, 2.0*y
init_pos = (-7.0, 2.0)
params = {}
params['x'], params['y'] = init_pos[0], init_pos[1]
grads = {}
grads['x'], grads['y'] = 0, 0
optimizers = OrderedDict()
#optimizers["SGD"] = SGD(lr=0.95)
optimizers["Momentum lr=0.2 α=1"] = Momentum(lr=0.2, momentum=1)
optimizers["Momentum lr=0.2 α=0.8"] = Momentum(lr=0.2, momentum=0.8)
optimizers["Momentum lr=0.95 α=0.1"] = Momentum(lr=0.95, momentum=0.1)
optimizers["SGD lr=0.95"] = SGD(lr=0.95)
#optimizers["AdaGrad"] = AdaGrad(lr=1.5)
#optimizers["Adam"] = Adam(lr=0.3)
idx = 1
plt.figure(figsize=(10,10))
for key in optimizers:
optimizer = optimizers[key]
x_history = []
y_history = []
params['x'], params['y'] = init_pos[0], init_pos[1]
for i in range(30):
x_history.append(params['x'])
y_history.append(params['y'])
grads['x'], grads['y'] = df(params['x'], params['y'])
optimizer.update(params, grads)
x = np.arange(-10, 10, 0.01)
y = np.arange(-5, 5, 0.01)
X, Y = np.meshgrid(x, y)
Z = f(X, Y)
# for simple contour line
mask = Z > 7
Z[mask] = 0
# plot
plt.subplot(2, 2, idx)
idx += 1
#plt.figure(figsize=(10,10))
plt.plot(x_history, y_history, 'o-', color="red")
plt.contour(X, Y, Z)
plt.ylim(-10, 10)
plt.xlim(-10, 10)
plt.plot(0, 0, '+')
#colorbar()
#spring()
plt.title(key)
plt.xlabel("x")
plt.ylabel("y")
plt.show()
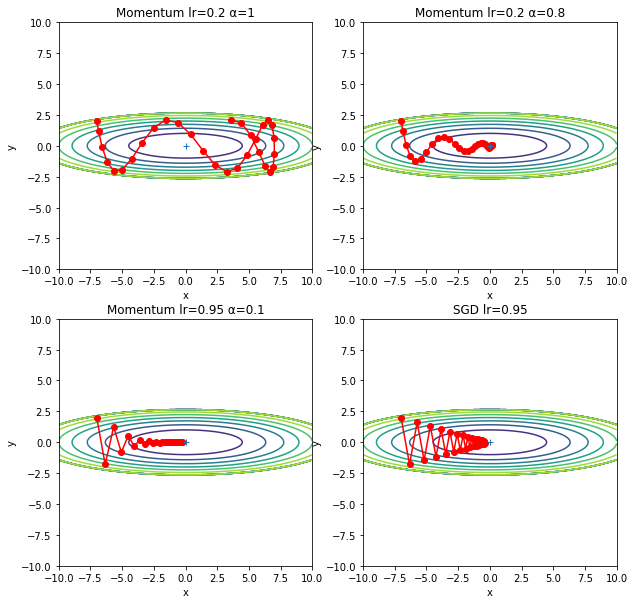
上图展示了在摩擦力 $\alpha$ 取不同值的情况下的搜索路径,以及与 SGD 的比较。可以很明显的看出, $\alpha$ 过大的话,惯性太强,会导致错过最低点,而如果 $\alpha$ 过小,就会导致摩擦力过小,从而退化成 SGD。
当 $\alpha$ 取值适中时,路径就像小球滑动一样,由于在y轴方向上速度相互抵消,x轴方向上速度则累积,所以路径有向 x 方向靠近的趋势。
这里要说明一下,图中几种方法的学习率并不完全一样。学习率一样的图如下:
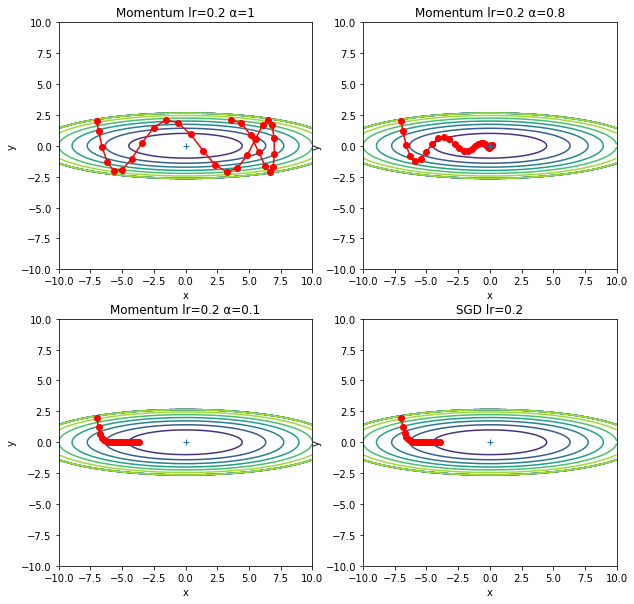
AdaGrad
AdaGrad 全称是 Adaptive Gradient,这种方法就是适当的调整学习率,使得学习率随着学习不断减小。用数学表示为:
\[\bd{h} \leftarrow \bd{h} + \frac{\partial L}{\partial \bd{W}} \odot \frac{\partial L}{\partial \bd{W}}\\ \bd{W} \leftarrow \bd{W} - \eta \frac{1}{\sqrt{\bd{h}}} \frac{\partial L}{\partial \bd{W}}\]$\odot$ 表示矩阵的对应元素相乘。$\bd{h}$ 会记录过去所有梯度的平方和,显然学习的次数越多,$\bd{h}$ 越大,则 $\eta \frac{1}{\sqrt{\bd{h}}}$ 越小。
class AdaGrad:
"""AdaGrad"""
def __init__(self, lr=0.01):
self.lr = lr
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] += grads[key] * grads[key]
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7) #1e-7 是为了避免出现除以0的情况
AdaGrad搜索最小值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
import numpy as np
import matplotlib.pyplot as plt
from collections import OrderedDict
def f(x, y):
return x**2 / 20.0 + y**2
def df(x, y):
return x / 10.0, 2.0*y
init_pos = (-7.0, 2.0)
params = {}
params['x'], params['y'] = init_pos[0], init_pos[1]
grads = {}
grads['x'], grads['y'] = 0, 0
optimizers = OrderedDict()
#optimizers["SGD"] = SGD(lr=0.95)
#optimizers["Momentum lr=0.2 α=1"] = Momentum(lr=0.2, momentum=1)
#optimizers["Momentum lr=0.2 α=0.8"] = Momentum(lr=0.2, momentum=0.8)
#optimizers["Momentum lr=0.2 α=0.1"] = Momentum(lr=0.2, momentum=0.1)
#optimizers["SGD lr=0.2"] = SGD(lr=0.2)
optimizers["AdaGrad"] = AdaGrad(lr=1.5)
#optimizers["Adam"] = Adam(lr=0.3)
idx = 1
for key in optimizers:
optimizer = optimizers[key]
x_history = []
y_history = []
params['x'], params['y'] = init_pos[0], init_pos[1]
for i in range(30):
x_history.append(params['x'])
y_history.append(params['y'])
grads['x'], grads['y'] = df(params['x'], params['y'])
optimizer.update(params, grads)
x = np.arange(-10, 10, 0.01)
y = np.arange(-5, 5, 0.01)
X, Y = np.meshgrid(x, y)
Z = f(X, Y)
# for simple contour line
mask = Z > 7
Z[mask] = 0
# plot
#plt.subplot(2, 2, idx)
#idx += 1
plt.figure(figsize=(5,5))
plt.plot(x_history, y_history, 'o-', color="red")
plt.contour(X, Y, Z)
plt.ylim(-10, 10)
plt.xlim(-10, 10)
plt.plot(0, 0, '+')
#colorbar()
#spring()
plt.title(key)
plt.xlabel("x")
plt.ylabel("y")
plt.show()
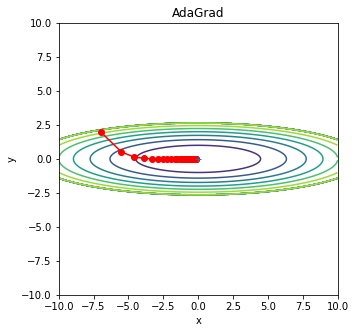
其他方法
Adma 将 Momentum 和 AdaGrad 结合在一起,同时加入超参数的“偏置校正”。但其代码有段复杂,在此不做解释。
class Adam:
"""Adam (http://arxiv.org/abs/1412.6980v8)"""
def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
self.lr = lr
self.beta1 = beta1
self.beta2 = beta2
self.iter = 0
self.m = None
self.v = None
def update(self, params, grads):
if self.m is None:
self.m, self.v = {}, {}
for key, val in params.items():
self.m[key] = np.zeros_like(val)
self.v[key] = np.zeros_like(val)
self.iter += 1
lr_t = self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter)
for key in params.keys():
#self.m[key] = self.beta1*self.m[key] + (1-self.beta1)*grads[key]
#self.v[key] = self.beta2*self.v[key] + (1-self.beta2)*(grads[key]**2)
self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
self.v[key] += (1 - self.beta2) * (grads[key]**2 - self.v[key])
params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)
#unbias_m += (1 - self.beta1) * (grads[key] - self.m[key]) # correct bias
#unbisa_b += (1 - self.beta2) * (grads[key]*grads[key] - self.v[key]) # correct bias
#params[key] += self.lr * unbias_m / (np.sqrt(unbisa_b) + 1e-7)
Adam搜索最小值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
import numpy as np
import matplotlib.pyplot as plt
from collections import OrderedDict
def f(x, y):
return x**2 / 20.0 + y**2
def df(x, y):
return x / 10.0, 2.0*y
init_pos = (-7.0, 2.0)
params = {}
params['x'], params['y'] = init_pos[0], init_pos[1]
grads = {}
grads['x'], grads['y'] = 0, 0
optimizers = OrderedDict()
#optimizers["SGD"] = SGD(lr=0.95)
#optimizers["Momentum lr=0.2 α=0.8"] = Momentum(lr=0.2, momentum=0.8)
#optimizers["SGD lr=0.2"] = SGD(lr=0.2)
#optimizers["AdaGrad"] = AdaGrad(lr=1.5)
optimizers["Adam"] = Adam(lr=0.3)
idx = 1
for key in optimizers:
optimizer = optimizers[key]
x_history = []
y_history = []
params['x'], params['y'] = init_pos[0], init_pos[1]
for i in range(30):
x_history.append(params['x'])
y_history.append(params['y'])
grads['x'], grads['y'] = df(params['x'], params['y'])
optimizer.update(params, grads)
x = np.arange(-10, 10, 0.01)
y = np.arange(-5, 5, 0.01)
X, Y = np.meshgrid(x, y)
Z = f(X, Y)
# for simple contour line
mask = Z > 7
Z[mask] = 0
# plot
#plt.subplot(2, 2, idx)
#idx += 1
plt.figure(figsize=(5,5))
plt.plot(x_history, y_history, 'o-', color="red")
plt.contour(X, Y, Z)
plt.ylim(-10, 10)
plt.xlim(-10, 10)
plt.plot(0, 0, '+')
#colorbar()
#spring()
plt.title(key)
plt.xlabel("x")
plt.ylabel("y")
plt.show()
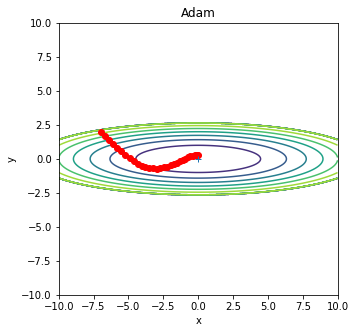
四种方法比较
这四种方法各有各的好处,目前大部分还是在用 SGD,很多研究人员也喜欢用 Adam。
4种方法比较
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
import numpy as np
import matplotlib.pyplot as plt
from collections import OrderedDict
def f(x, y):
return x**2 / 20.0 + y**2
def df(x, y):
return x / 10.0, 2.0*y
init_pos = (-7.0, 2.0)
params = {}
params['x'], params['y'] = init_pos[0], init_pos[1]
grads = {}
grads['x'], grads['y'] = 0, 0
optimizers = OrderedDict()
optimizers["SGD"] = SGD(lr=0.95)
optimizers["Momentum"] = Momentum(lr=0.1)
optimizers["AdaGrad"] = AdaGrad(lr=1.5)
optimizers["Adam"] = Adam(lr=0.3)
idx = 1
plt.figure(figsize=(10,10))
for key in optimizers:
optimizer = optimizers[key]
x_history = []
y_history = []
params['x'], params['y'] = init_pos[0], init_pos[1]
for i in range(30):
x_history.append(params['x'])
y_history.append(params['y'])
grads['x'], grads['y'] = df(params['x'], params['y'])
optimizer.update(params, grads)
x = np.arange(-10, 10, 0.01)
y = np.arange(-5, 5, 0.01)
X, Y = np.meshgrid(x, y)
Z = f(X, Y)
# for simple contour line
mask = Z > 7
Z[mask] = 0
# plot
plt.subplot(2, 2, idx)
idx += 1
plt.plot(x_history, y_history, 'o-', color="red")
plt.contour(X, Y, Z)
plt.ylim(-10, 10)
plt.xlim(-10, 10)
plt.plot(0, 0, '+')
#colorbar()
#spring()
plt.title(key)
plt.xlabel("x")
plt.ylabel("y")
plt.show()
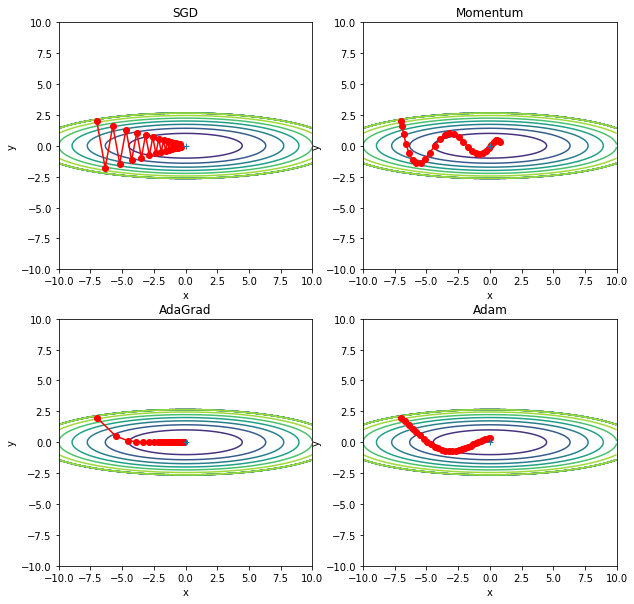
多层神经网络
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
import numpy as np
from collections import OrderedDict
class MultiLayerNet:
"""全连接的多层神经网络
Parameters
----------
input_size : 输入大小(MNIST的情况下为784)
hidden_size_list : 隐藏层的神经元数量的列表(e.g. [100, 100, 100])
output_size : 输出大小(MNIST的情况下为10)
activation : 'relu' or 'sigmoid'
weight_init_std : 指定权重的标准差(e.g. 0.01)
指定'relu'或'he'的情况下设定“He的初始值”
指定'sigmoid'或'xavier'的情况下设定“Xavier的初始值”
weight_decay_lambda : Weight Decay(L2范数)的强度
"""
def __init__(self, input_size, hidden_size_list, output_size,
activation='relu', weight_init_std='relu', weight_decay_lambda=0):
self.input_size = input_size
self.output_size = output_size
self.hidden_size_list = hidden_size_list
self.hidden_layer_num = len(hidden_size_list)
self.weight_decay_lambda = weight_decay_lambda
self.params = {}
# 初始化权重
self.__init_weight(weight_init_std)
# 生成层
activation_layer = {'sigmoid': Sigmoid, 'relu': Relu}
self.layers = OrderedDict()
for idx in range(1, self.hidden_layer_num+1):
self.layers['Affine' + str(idx)] = Affine(self.params['W' + str(idx)],
self.params['b' + str(idx)])
self.layers['Activation_function' + str(idx)] = activation_layer[activation]()
idx = self.hidden_layer_num + 1
self.layers['Affine' + str(idx)] = Affine(self.params['W' + str(idx)],
self.params['b' + str(idx)])
self.last_layer = SoftmaxWithLoss()
def __init_weight(self, weight_init_std):
"""设定权重的初始值
Parameters
----------
weight_init_std : 指定权重的标准差(e.g. 0.01)
指定'relu'或'he'的情况下设定“He的初始值”
指定'sigmoid'或'xavier'的情况下设定“Xavier的初始值”
"""
all_size_list = [self.input_size] + self.hidden_size_list + [self.output_size]
for idx in range(1, len(all_size_list)):
scale = weight_init_std
if str(weight_init_std).lower() in ('relu', 'he'):
scale = np.sqrt(2.0 / all_size_list[idx - 1]) # 使用ReLU的情况下推荐的初始值
elif str(weight_init_std).lower() in ('sigmoid', 'xavier'):
scale = np.sqrt(1.0 / all_size_list[idx - 1]) # 使用sigmoid的情况下推荐的初始值
self.params['W' + str(idx)] = scale * np.random.randn(all_size_list[idx-1], all_size_list[idx])
self.params['b' + str(idx)] = np.zeros(all_size_list[idx])
def predict(self, x):
for layer in self.layers.values():
x = layer.forward(x)
return x
def loss(self, x, t):
"""求损失函数
Parameters
----------
x : 输入数据
t : 教师标签
Returns
-------
损失函数的值
"""
y = self.predict(x)
weight_decay = 0
for idx in range(1, self.hidden_layer_num + 2):
W = self.params['W' + str(idx)]
weight_decay += 0.5 * self.weight_decay_lambda * np.sum(W ** 2)
return self.last_layer.forward(y, t) + weight_decay
def accuracy(self, x, t):
y = self.predict(x)
y = np.argmax(y, axis=1)
if t.ndim != 1 : t = np.argmax(t, axis=1)
accuracy = np.sum(y == t) / float(x.shape[0])
return accuracy
def numerical_gradient(self, x, t):
"""求梯度(数值微分)
Parameters
----------
x : 输入数据
t : 教师标签
Returns
-------
具有各层的梯度的字典变量
grads['W1']、grads['W2']、...是各层的权重
grads['b1']、grads['b2']、...是各层的偏置
"""
loss_W = lambda W: self.loss(x, t)
grads = {}
for idx in range(1, self.hidden_layer_num+2):
grads['W' + str(idx)] = numerical_gradient(loss_W, self.params['W' + str(idx)])
grads['b' + str(idx)] = numerical_gradient(loss_W, self.params['b' + str(idx)])
return grads
def gradient(self, x, t):
"""求梯度(误差反向传播法)
Parameters
----------
x : 输入数据
t : 教师标签
Returns
-------
具有各层的梯度的字典变量
grads['W1']、grads['W2']、...是各层的权重
grads['b1']、grads['b2']、...是各层的偏置
"""
# forward
self.loss(x, t)
# backward
dout = 1
dout = self.last_layer.backward(dout)
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
# 设定
grads = {}
for idx in range(1, self.hidden_layer_num+2):
grads['W' + str(idx)] = self.layers['Affine' + str(idx)].dW + self.weight_decay_lambda * self.layers['Affine' + str(idx)].W
grads['b' + str(idx)] = self.layers['Affine' + str(idx)].db
return grads
用4种方法训练神经网络
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
# 0:读入MNIST数据==========
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)
train_size = x_train.shape[0]
batch_size = 128
max_iterations = 2000
# 1:进行实验的设置==========
optimizers = {}
optimizers['SGD'] = SGD()
optimizers['Momentum'] = Momentum()
optimizers['AdaGrad'] = AdaGrad()
optimizers['Adam'] = Adam()
#optimizers['RMSprop'] = RMSprop()
networks = {}
train_loss = {}
for key in optimizers.keys():
networks[key] = MultiLayerNet(
input_size=784, hidden_size_list=[100, 100, 100, 100],
output_size=10)
train_loss[key] = []
# 2:开始训练==========
for i in range(max_iterations):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
for key in optimizers.keys():
grads = networks[key].gradient(x_batch, t_batch)
optimizers[key].update(networks[key].params, grads)
loss = networks[key].loss(x_batch, t_batch)
train_loss[key].append(loss)
if i % 100 == 0:
print( "===========" + "iteration:" + str(i) + "===========")
for key in optimizers.keys():
loss = networks[key].loss(x_batch, t_batch)
print(key + ":" + str(loss))
# 3.绘制图形==========
markers = {"SGD": "o", "Momentum": "x", "AdaGrad": "s", "Adam": "D"}
x = np.arange(max_iterations)
for key in optimizers.keys():
plt.plot(x, smooth_curve(train_loss[key]), marker=markers[key], markevery=100, label=key)
plt.xlabel("iterations")
plt.ylabel("loss")
plt.ylim(0, 1)
plt.legend()
plt.show()
训练过程
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
OUTPUT:
===========iteration:0===========
SGD:2.3485739917108637
Momentum:2.3522046522492794
AdaGrad:2.09596243880509
Adam:2.286168134839006
===========iteration:100===========
SGD:1.6737021818918079
Momentum:0.34304437641185453
AdaGrad:0.09744134360533335
Adam:0.21940551777853826
===========iteration:200===========
SGD:0.9104381165995677
Momentum:0.1873309205345749
AdaGrad:0.10002099602063744
Adam:0.1292136135227925
===========iteration:300===========
SGD:0.7283782378846393
Momentum:0.3225125565712884
AdaGrad:0.15720771302985487
Adam:0.21638674225543547
===========iteration:400===========
SGD:0.391455496853796
Momentum:0.1029791678320692
AdaGrad:0.058029357107012264
Adam:0.058460664481003934
===========iteration:500===========
SGD:0.35312427699249405
Momentum:0.11811551694219022
AdaGrad:0.05317992225784239
Adam:0.0975733073952009
===========iteration:600===========
SGD:0.3968798142346487
Momentum:0.13257770306109418
AdaGrad:0.04442060488233331
Adam:0.06868626113583051
===========iteration:700===========
SGD:0.3683953439290294
Momentum:0.15152190079116779
AdaGrad:0.06388558938436376
Adam:0.10100017214926185
===========iteration:800===========
SGD:0.31943197656519123
Momentum:0.1319509632442575
AdaGrad:0.04192396391023745
Adam:0.11770353676781588
===========iteration:900===========
SGD:0.3269274916359882
Momentum:0.09585866951832829
AdaGrad:0.05772451068732593
Adam:0.0343196737176152
===========iteration:1000===========
SGD:0.3060900068921663
Momentum:0.09918598088118444
AdaGrad:0.03386238334915528
Adam:0.02745157158624999
===========iteration:1100===========
SGD:0.24604785231249626
Momentum:0.0765639623922497
AdaGrad:0.02859494660960913
Adam:0.06036465451684854
===========iteration:1200===========
SGD:0.24549876602474874
Momentum:0.08258567555967523
AdaGrad:0.024888633710375824
Adam:0.03387290564119953
===========iteration:1300===========
SGD:0.2836878048565276
Momentum:0.08895278725160284
AdaGrad:0.03653546679207839
Adam:0.05309919734119551
===========iteration:1400===========
SGD:0.23085958304658483
Momentum:0.03847219599586724
AdaGrad:0.016188521565713394
Adam:0.02099214308265244
===========iteration:1500===========
SGD:0.2157182235346113
Momentum:0.0630373914672752
AdaGrad:0.05751162227571255
Adam:0.03173034288883679
===========iteration:1600===========
SGD:0.2156077115468094
Momentum:0.11938716344173866
AdaGrad:0.03376159561335184
Adam:0.030634519847923584
===========iteration:1700===========
SGD:0.2196324551184294
Momentum:0.0565591881758724
AdaGrad:0.035413723353518625
Adam:0.03618776840878777
===========iteration:1800===========
SGD:0.27904908991529087
Momentum:0.05253914340265198
AdaGrad:0.028402182128005132
Adam:0.037956770759634814
===========iteration:1900===========
SGD:0.14365472812448798
Momentum:0.03325477934942276
AdaGrad:0.02150331702778522
Adam:0.023888622257909737
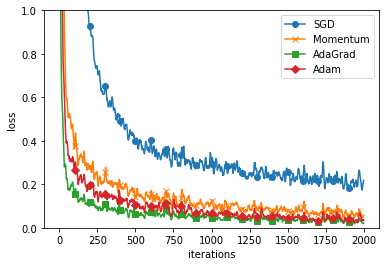
权重的初始值
不能将权重初始值设为0
隐藏层的激活值分布
隐藏层的激活值指的是激活函数的输出数据。下面来做一个实验,实验过程如下:
- 构造一个5层神经网络,每个网络有100个节点,参数随机初始化
- 随机构造1000个数据
- 将数据输入到网络,看看每层的激活值的分布
实验代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
import numpy as np
import matplotlib.pyplot as plt
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def ReLU(x):
return np.maximum(0, x)
def tanh(x):
return np.tanh(x)
input_data = np.random.randn(1000, 100) # 1000个数据
node_num = 100 # 各隐藏层的节点(神经元)数
hidden_layer_size = 5 # 隐藏层有5层
activations = {} # 激活值的结果保存在这里
x = input_data
for i in range(hidden_layer_size):
if i != 0:
x = activations[i-1]
# 改变初始值进行实验!
w = np.random.randn(node_num, node_num) * 1
# w = np.random.randn(node_num, node_num) * 0.01
# w = np.random.randn(node_num, node_num) * np.sqrt(1.0 / node_num)
# w = np.random.randn(node_num, node_num) * np.sqrt(2.0 / node_num)
a = np.dot(x, w)
# 将激活函数的种类也改变,来进行实验!
z = sigmoid(a)
# z = ReLU(a)
# z = tanh(a)
activations[i] = z
# 绘制直方图
for i, a in activations.items():
plt.subplot(1, len(activations), i+1)
plt.title(str(i+1) + "-layer")
if i != 0: plt.yticks([], [])
# plt.xlim(0.1, 1)
# plt.ylim(0, 7000)
plt.hist(a.flatten(), 30, range=(0,1))
plt.show()

当初始化权重采用标准差为1的高斯分布时,由图中可以看出,Sigmoid 函数的输出靠近0和1,回想Sigmoid函数图像的特点,y越是靠近0和1,梯度越小甚至会消失。这个问题称为 梯度消失。层次越深,梯度消失问题越严重。
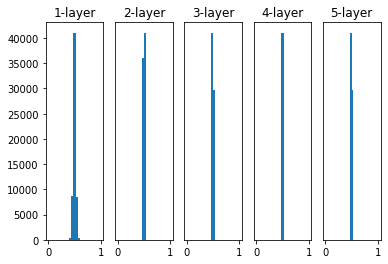
如果改为使用标准差为 0.01 的高斯分布,激活值分布如图,集中在 0.5 附近,这说明网络的表现力有很大问题,因为如果多个神经元的输出都差不多,那为什么不用一个神经元代替呢?这样多个神经元就没有意义了。
要设置合适的权重,可以采用 Xavier 等人提出的 Xavier 初始值,即如果前一层的节点数为 $n$,则初始值使用标准差为 $\frac{1}{\sqrt{n}}$ 的分布。
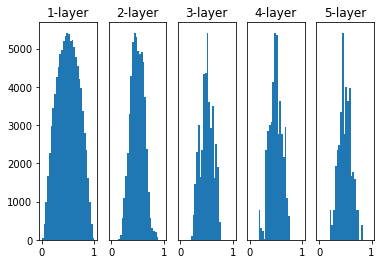
可以看出,越是后面的层,图像越是歪斜、集中,但都比前两次实验好,这样 sigmoid 的表现力不受限制,可以进行高效的学习。把激活函数换成 tanh 的话,和 Sigmoid 类似,也是使用 Xavier 初始值。
如果将激活函数换成 ReLU,则推荐使用 He初始值:初始值使用标准差为 $\frac{2}{\sqrt{n}}$ 的分布。直观上可以认为,ReLU 负值区域的值为0,要使其更有广度,需要 2 倍系数。

下面看看不同初始值的幅值方法在多大程度上影响神经网络的学习:
不同初始值神经网络对比
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
import numpy as np
import matplotlib.pyplot as plt
# 0:读入MNIST数据==========
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)
train_size = x_train.shape[0]
batch_size = 128
max_iterations = 2000
# 1:进行实验的设置==========
weight_init_types = {'std=0.01': 0.01, 'Xavier': 'sigmoid', 'He': 'relu'}
optimizer = SGD(lr=0.01)
networks = {}
train_loss = {}
for key, weight_type in weight_init_types.items():
networks[key] = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100],
output_size=10, weight_init_std=weight_type)
train_loss[key] = []
# 2:开始训练==========
for i in range(max_iterations):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
for key in weight_init_types.keys():
grads = networks[key].gradient(x_batch, t_batch)
optimizer.update(networks[key].params, grads)
loss = networks[key].loss(x_batch, t_batch)
train_loss[key].append(loss)
if i % 100 == 0:
print("===========" + "iteration:" + str(i) + "===========")
for key in weight_init_types.keys():
loss = networks[key].loss(x_batch, t_batch)
print(key + ":" + str(loss))
# 3.绘制图形==========
markers = {'std=0.01': 'o', 'Xavier': 's', 'He': 'D'}
x = np.arange(max_iterations)
for key in weight_init_types.keys():
plt.plot(x, smooth_curve(train_loss[key]), marker=markers[key], markevery=100, label=key)
plt.xlabel("iterations")
plt.ylabel("loss")
plt.ylim(0, 2.5)
plt.legend()
plt.show()
训练过程
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
OUTPUT:
===========iteration:0===========
std=0.01:2.302488098394867
Xavier:2.313991861232406
He:2.379480621555028
===========iteration:100===========
std=0.01:2.301946884429742
Xavier:2.2759217861258234
He:1.5404494857149582
===========iteration:200===========
std=0.01:2.303139397799229
Xavier:2.191849922446238
He:0.8991489947624611
===========iteration:300===========
std=0.01:2.3040541960447047
Xavier:2.016783792641773
He:0.48854931051925543
===========iteration:400===========
std=0.01:2.3021457045022773
Xavier:1.5923141443350293
He:0.40391016489106313
===========iteration:500===========
std=0.01:2.301867924364439
Xavier:1.087718167226913
He:0.3346890028961583
===========iteration:600===========
std=0.01:2.2981436052064783
Xavier:0.7184081251134143
He:0.26243148305132696
===========iteration:700===========
std=0.01:2.302637321415247
Xavier:0.6704853185787227
He:0.32589530836927005
===========iteration:800===========
std=0.01:2.3015025938329865
Xavier:0.5503642928247523
He:0.2696782240186154
===========iteration:900===========
std=0.01:2.3041182466932795
Xavier:0.4853297165610774
He:0.2396549348459854
===========iteration:1000===========
std=0.01:2.303380368142644
Xavier:0.4954993986573032
He:0.36665900135510143
===========iteration:1100===========
std=0.01:2.2937498539779586
Xavier:0.45716252360709186
He:0.2726996073957305
===========iteration:1200===========
std=0.01:2.3012445320200876
Xavier:0.2714963148598767
He:0.1595216332703695
===========iteration:1300===========
std=0.01:2.302259964534186
Xavier:0.32168194272662776
He:0.16999941975439864
===========iteration:1400===========
std=0.01:2.3024362421537288
Xavier:0.32395054604056395
He:0.16777840230844226
===========iteration:1500===========
std=0.01:2.307860834243974
Xavier:0.3166015810113228
He:0.21018365502156464
===========iteration:1600===========
std=0.01:2.304330721184222
Xavier:0.42670618997914966
He:0.26763184069698653
===========iteration:1700===========
std=0.01:2.295479004155304
Xavier:0.2874124967868307
He:0.19237106286663852
===========iteration:1800===========
std=0.01:2.2996740529123754
Xavier:0.31069994110374644
He:0.22572573237078394
===========iteration:1900===========
std=0.01:2.297923361908695
Xavier:0.2401290997148865
He:0.20426176553129521
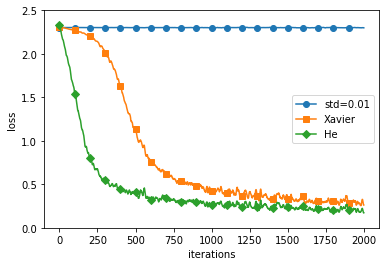
可以看出,使用 Xavier 和 He 都能较快收敛,而0.01高斯分布则非常菜……
Batch Normalization
这是一种比较新的方法(2015年提出),它具有以下优点:
- 可以使学习快速进行
- 不那么依赖初始值
- 抑制过拟合
其原理是这样的:对 mini-batch 的 $m$ 个输入 ${x_1,x_2,\cdots,x_m}$ 进行正规化,变换为均值为0,方差为1的数据 ${\hat{x}_1,\hat{x}_2,\cdots,\hat{x}_m}$,然后对正规化的数据进行缩放和平移:$y_i \leftarrow \gamma \hat{x}_i+\beta$
正规化的公式如下:
\[\mu_B \leftarrow \frac{1}{m} \sum_{i=1}^m x_i\\ \sigma_B^2 \leftarrow \frac{1}{m} \sum_{i=1}^m (x_i-\mu_B)^2\\ \hat{x}_i \leftarrow \frac{x_i - \mu_B}{\sqrt{\sigma_B^2 + \varepsilon}}\]Batch Norm 一般在激活函数前后,可以减小数据分布的偏向。