\[\newcommand{\dif}{\mathop{}\!\mathrm{d}} \newcommand{\p}{\partial}\]

方向导数

定义等势面

$D \in \mathbb{R}^n$，$x\in D \rightarrow f(x)\in \mathbb{R}$，则 $D$ 中有数量场 $f$，并且我们将 $S={x\in D \vert f(x)=C,C\in\mathbb{R}}$ 称为等势面（等位面）

定义方向导数

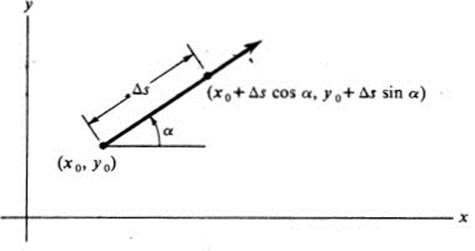
设 $P_0(x_0,y_0)\in D \subset \mathbb{R}^2$，$\vec{l}={\cos\alpha, \sin\alpha}$

过 $P_0,\vec{l}$方向的直线 :

\[L=\begin{cases} x=x_0+\cos\alpha\cdot t\\ y=y_0+\sin\alpha\cdot t \end{cases}\]

其中$t$ 为参数。或简写为：$P=t\vec{l}+P_0$

若 $\lim_{t\rightarrow 0} \frac{f(P_0+t\vec{l})-f(P_0)}{t}$ 存在，则称为 $f(x,y)$ 在 $P_0$ 沿 $\vec{l}$ 方向的方向导数，记为 $\frac{\p f}{\p \vec{l}} \Big\vert_{P_0}$ 或 $\frac{\p f(P_0)}{\p \vec{l}}$

令 $f(x_0+t\cos x, y_0+t\sin\alpha)=\varphi(t)$，则上式可写为：$\lim_{t\rightarrow 0} \frac{\varphi(t)-\varphi(0)}{t}=\varphi’(t)$

若 $f$ 在 $(x_0,y_0)$ 可微，则 $\varphi’(t)=\frac{\p f}{\p x}\cos\alpha+\frac{\p f}{\p y}\sin\alpha$。可见，偏导数就是特殊的方向导数。

以上可以推广到三元、多元函数。

梯度

定义梯度

\[设\begin{cases} u=f(x,y,z)\\ \vec{g}=\text{grad}f(P_0)=\{ \dfrac{\p f}{\p x}, \dfrac{\p f}{\p y}, \dfrac{\p f}{\p z}\}_{P_0}\\ \vec{l}=\{ \cos\alpha, \cos\beta, \cos\gamma \} \end{cases}\]

则：$\frac{\p f}{\p\vec{l}}=\vec{g}\cdot\vec{l}=\vert\vec{g}\vert\cdot\vert\vec{l}\vert\cdot\cos<\vec{g},\vec{l}>$$=\vert\vec{g}\vert\cdot\cos<\vec{g},\vec{l}>$

显然，当 $\cos<\vec{g},\vec{l}>=1$ 时，$\frac{\p f}{\p \vec{l}}$ 最大。

综上，若 $\text{grad}f(P_0)=\vec{0}$，则 $\frac{\p f}{\p \vec{l}}\big\vert_{P_0}=0$. 若 $\text{grad}f(P_0)\neq\vec{0}$，则当 $\vec{l}=\dfrac{\text{grad}f}{\vert\text{grad}f\vert}$时，$\frac{\p f}{\p \vec{l}}\big\vert_{P_0}$ 最大；当 $\vec{l}=-\dfrac{\text{grad}f}{\vert\text{grad}f\vert}$时，$\frac{\p f}{\p \vec{l}}\big\vert_{P_0}$ 最小。

故我们定义 $\frac{\p f}{\p x}\vec{i}+\frac{\p f}{\p y}\vec{j}+\frac{\p f}{\p z}\vec{k}$ 为梯度向量（梯度），记为 $\text{grad}f$ 或 $\nabla f$（是一个向量），方向导数为 $\nabla f$ 在 $\vec{l}$ 方向的投影

注释

运算法则：

1. $\nabla C=\vec{0}$
2. $\nabla(Cf)=C\nabla f$
3. $\nabla(f\pm g)=\nabla f\pm \nabla g$
4. $\nabla(fg)=(\nabla f)\cdot g+(\nabla g)\cdot f$
5. $\nabla(f(u))=f’(u)\cdot\nabla u,\;u=u(x,y,z)$