目标
- 认识 Fibonacci 数列,体验发现其通项公式的过程。
- 了解 matlab 软件中,进行数据显示与数据拟合的方式。
- 提高对数据进行分析与处理的能力。
斐波那契数列
斐波那契数列(Fibonacci sequence)定义为:
\[F_0=0\\ F_1=1\\ F_2=F_0+F_1=1\\ F_3=F_1+F_2=2\\ \cdots\\ F_n=F_{n-1}+F_{n-2}, n\geq2\]实验过程
- 观察数据间的大概函数关系
- 进一步验证上一步得到的结论
- 获得数据的近似函数关系式
- 观察拟合数据与原始数据的吻合程度
- 猜测 Fibonacci 数列的通项公式
- 证明 Fibonacci 数列的通项公式
观察数据间的大概函数关系
我们编写如下函数:
x=[1:30];
y=fibonacci(x);
scatter(x,y,20);
得到的图像为:
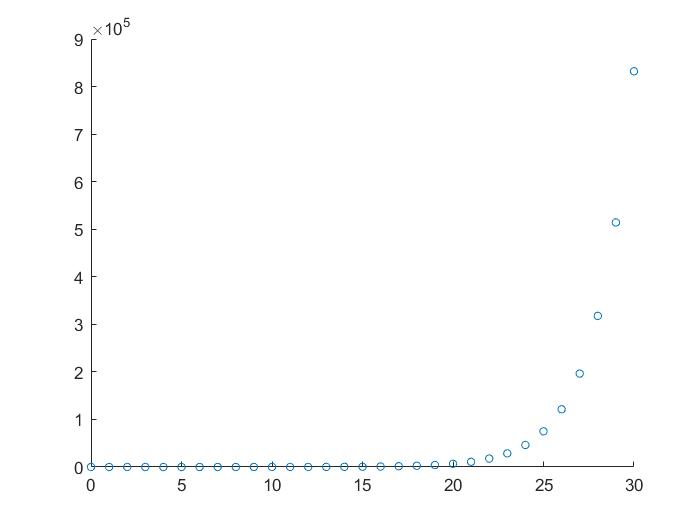
进一步验证上一步得到的结论
我们可以尝试对 y 进行处理,比如取对数:
x=[1:30];
y1=log(fibonacci(x));
scatter(x,y1,20),
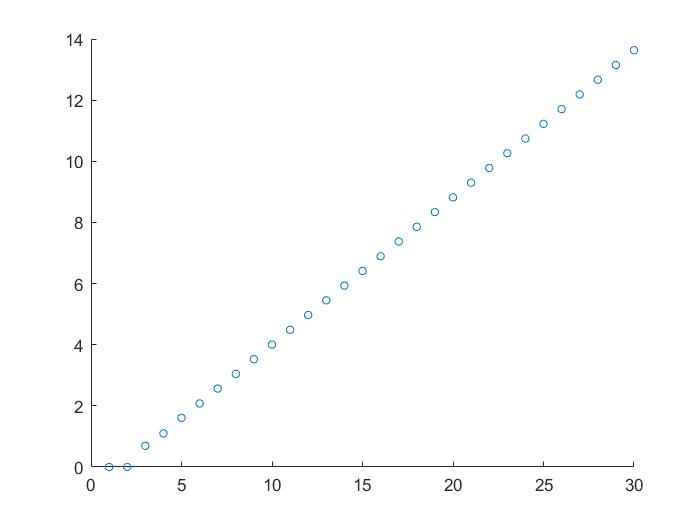
获得数据的近似函数关系式
可以发现,这个近似于一条直线,所以我们尝试用一次函数进行拟合:
x=[1:1000];
y1=log(fibonacci(x));
p=polyfit(x,y1,1)
得到:p = 0.4812 -0.8039,从而 $F_n=e^{0.4812x-0.8039}=0.4476\times1.618^x$
观察拟合数据与原始数据的吻合程度
作出拟合图像,发现还是挺好的。
x=[1:50];
y=fibonacci(x);
y_fit=0.4476*1.619.^x;
plot(x,y,':o',x,y_fit,'-*')
legend('fibonacci','polyfit')
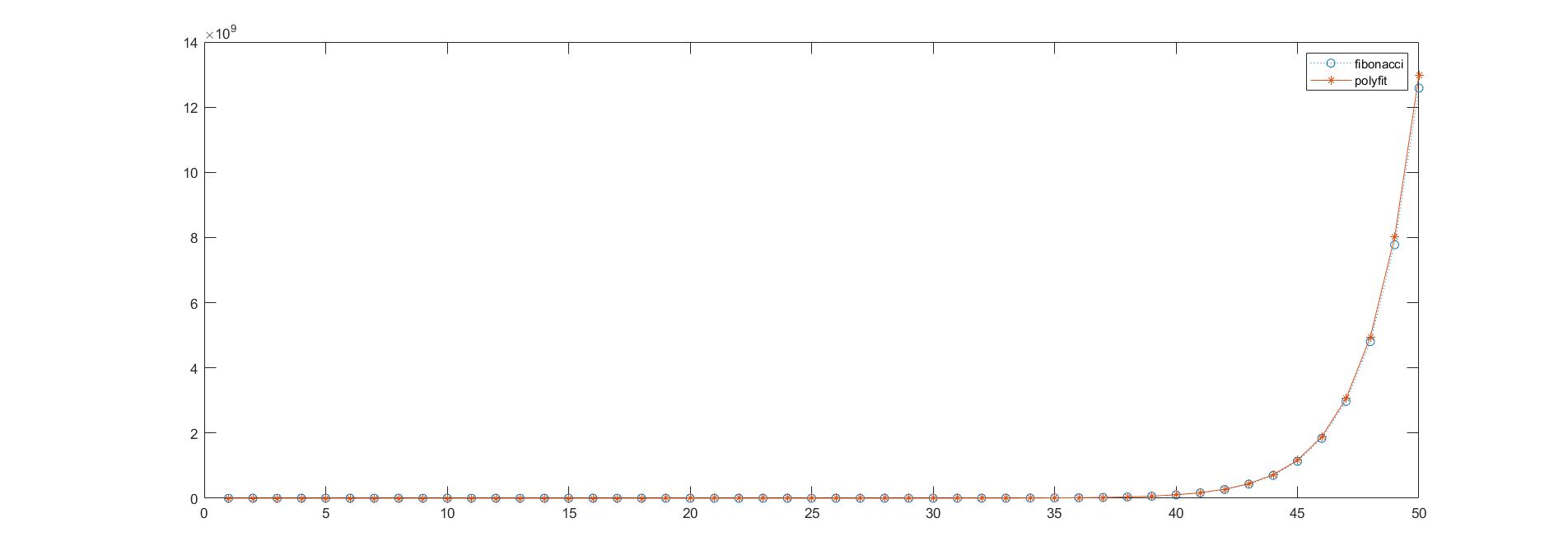
猜测 Fibonacci 数列的通项公式
可以猜测 $F_n=Cr^n$,代入递推公式得 $r^2-r-1=0$,解得:
\[r_{1,2}=\frac{1\pm\sqrt{5}}{2}\]所以我们猜 $F_n=C\big( \frac{1+\sqrt{5}}{2} \big)^n$,然而不满足 $F_1=F_2=1$。所以我们令 $b_n=F_n-Cr^n$,可得数列 $b_n$ 应该也满足递推公式,猜测 $b_n=\bar{C}\bar{r}^n$,其中,$\bar{r}$ 也满足 $r^2=r+1$。最终得到:
\[F_n=Cr^n+\bar{C}\bar{r}^n=\frac{1}{\sqrt{5}}\left[ (\frac{1+\sqrt{5}}{2})^n-(\frac{1-\sqrt{5}}{2})^n \right]\]称为比内公式(Bint,1843).