迭代与分形
迭代就是将一种规则反复作用在某个对象上,通过迭代就能得到分形(fractal) 。

对于图形迭代,给定初始图形F0,以及一个替换规则R, 将R反复作用在初始图形F0上, 产生一个图形序列:
\[R(F_0)=F_1\\ R(F_1)=F_2\\ R(F_2)=F_3 \cdots\]其极限图形就是分形。(称R为生成元) 。
同理,对于函数迭代,给定初始值x0,以及一个函数f(x), 将f(x)反复作用在初始值x0上,产生一个数列:
\[F(x_0)=x_1\\ F(x_1)=x_2\\ F(x_2)=x_3 \cdots\]分形几何体的长度是无穷大,但面积却为零。所以如果用一维的线段去量,得数无穷大,尺子太小;用二维的正方形去量,得数为零,尺子又太大。所以维数介于 1 与 2 之间。为了衡量,我们定义相似维数:
设分形 F 是自相似的,F 由 m 个子集构成,每个子集放大 c 倍后同 F 相同,则 F 的维数为:
\[d=\frac{\ln m}{\ln c }\]对于通常的几何对象,相似维数与传统的维数是一致的。
实验过程
本实验以迭代的方式,来体验生成分形图的过程,从而对分形几何有一个直观的了解,并感受美丽的分形图案。
Koch曲线

可以看出,Koch 曲线每次迭代,都将每条线段替换为 Order 1。每次迭代,长度都增加 1/3。
Matlab代码
function plotkoch(k) %显示迭代k次后的Koch曲线图
p=[0,0;10,0]; %存放结点坐标,每行一个点,初始值为两结点的坐标
n=1; %存放线段的数量,初始值为1(思考:n若为结点数,后续该如何处理
A=[cos(pi/3),-sin(pi/3);sin(pi/3),cos(pi/3)]; %用于计算新的结点%旋转
for s=1:k %实现迭代过程,计算所有的结点的坐标
j=0; % 思考:可否取为1
%以下根据线段两个结点的坐标,计算迭代后它们之间增加的三个
%结点的坐标,并且将这些点的坐标按次序存暂时放到r中
for i=1:n %每条边计算一次
q1=p(i,:); %目前线段的起点坐标
q2=p(i+1,:); %目前线段的终点坐标
d=(q2-q1)/3;
j=j+1;r(j,:)=q1; %原起点存入r
j=j+1;r(j,:)=q1+d; %新1点存入r
j=j+1;r(j,:)=q1+d+d*A'; %新2点存入r
j=j+1;r(j,:)=q1+2*d; %新3点存入r
end %原终点作为下条线段的起点,在迭代下条线段时存入r
n=4*n; %全部线段迭代一次后,线段数量乘4
clear p %清空p ,注意:最后一个终点q2不在r中
p=[r;q2]; %重新装载本次迭代后的全部结点
end
figure
plot(p(:,1),p(:,2)) %显示各结点的连线图
axis equal %各坐标轴同比例(思考:若没有这项操作会怎样?)
另一种思路:
function koch(k)
p=[0 10]; %存放结点坐标
for m=1:k %实现迭代过程,计算所有的结点的坐标
q1=p/3; %将上一次迭代结果缩小到1/3
q2=10/3+(q1*exp(i*pi/3)); %斜向右上部分
q3=(10/3+10/3*exp(1i*pi/3))+(q1*exp(-1i*pi/3)); %斜向右下部分
q4=20/3+p/3; %右边水平部分
p=[q1 q2 q3 q4];
end
figure
plot(p) %显示各结点的连线图
axis equal %各坐标轴同比例
课后练习
Koch雪花
对一个等边三角形,每条边按照 Koch 曲线的方式进行迭代,产生的图形即为 Koch 雪花。我们只需要先得到一条 Koch 曲线,然后进行旋转、平移即可。
function koch(k)
p=[0 10]; %存放结点坐标
for m=1:k %实现迭代过程,计算所有的结点的坐标
q1=p/3; %将上一次迭代结果缩小到1/3
q2=10/3+(q1*exp(i*pi/3)); %斜向右上部分
q3=(10/3+10/3*exp(1i*pi/3))+(q1*exp(-1i*pi/3)); %斜向右下部分
q4=20/3+p/3; %右边水平部分
p=[q1 q2 q3 q4];
end
p1=p*exp(2*i*pi/3)+5-5*sqrt(3)*i; %逆时针旋转120度后平移
p2=p;
p3=p*exp(-2*i*pi/3)+10; %顺时针旋转120度后平移
p_all=[p1 p2 p3];
figure
plot(p_all) %显示各结点的连线图
axis equal %各坐标轴同比例

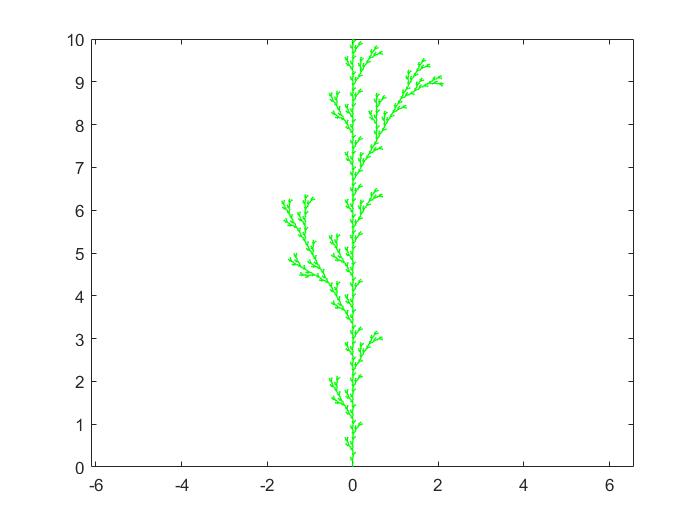
树
对一条竖向线段,在其三分之一分点处,向坐上方画一条线段,在其三分之二处,向右上方画一条线段,线段长度都是原来的三分之一,夹角都是 30°。
function koch(k)
p=[0 1i*10]; %存放结点坐标
for m=1:k %实现迭代过程,计算所有的结点的坐标
q1=p/3; %将上一次迭代结果缩小到1/3
q2=1i*10/3+(q1*exp(1i*pi/6)); %斜向左上部分
q3=1i*10/3+q1; %斜向右下部分
q4=1i*20/3+(q1*exp(-1i*pi/6)); %斜向右上部分
q5=1i*20/3+q1;
p=[q1 q2 q3 q4 q5];
end
figure
plot(p, 'g') %显示各结点的连线图
axis equal %各坐标轴同比例
hold off
下篇软件