深度学习概述

机器学习与深度学习

机器学习（machining Learning） 是对研究问题进行模型假设，利用计算机从训练数据中的到模型参数，并最终对数据进行预测和分析的一门学科。

深度学习（Deep Learning） 则是一种实现机器学习的技术，从属于机器学习。其主要是通过神经网络，通过组合底层特征形成更加抽象的高层特征。深度学习网络一般包括输入层、隐藏层、输出层。

数据集及其拆分

以 Iris（鸢尾花）数据集 为例，这个数据集包括三种花：山鸢尾、变色鸢尾、维吉尼亚鸢尾，我们根据花萼（sepal）和花瓣（petal）的长宽对鸢尾花进行分类。

鸢尾花数据集包括 4 个特征和 1 个类型标签：

Features
- Sepal Length
- Sepal Width
- Petal Length
- Petal Width
Class Label

一般的数据集可以表示为： ${ (x_1, y_1), (x_2, y_2), \cdots (x_n, y_n)}$，$x_i$ 为样本特征，是一个向量，而 $y_i$ 则表示样本的类别（也称为标签）。

如果训练过程中用到了样本标签，则称为 有监督学习。在有监督学习中，数据集通常分为 训练集（training set）、测试集（testing set），前者用于训练模型，后者用于评价模型。有时候会将训练集进一步分为 训练集 和 验证集（validation set），验证集用于在多个模型中进行选择。

训练集的划分方法有如下几种：

留出法（Hold-Out Method），将数据集随机地分为两组
- 优点是处理简单；缺点是性能评估结果依赖数据地拆分情况，不够稳定。
K折交叉验证，将数据集分为 K 份（K 一般取 5/10），每次用其中一个做测试集，其他做训练集，得到 K 个评价，取均值后得到最终评价结果。（PS. 每次训练都是从 0 开始，而不是从上一次开始）
- 优点是提高了评估结果地稳定性
分层抽样策略（Stratified k-fold） 在 K折交叉验证的基础上，使得每一份内各个类型数据的比例和原始数据集中各个类型的比例相同。

超参数 是指学习过程之前需要设定的一些变量，而不是训练得到的参数。比如学习速率就是超参数。我们可以通过 网格搜索，即找出所有超参数的组合，然后结合 K 折交叉验证，得到最好的超参数。

分类问题

分类问题 要解决的是预测样本属于哪个类，输出变量一般是有限个离散值。

分类的机器学习包括两个阶段：（1）从训练数据中得到分类模型，也就是 分类器（classifier）；（2）用分类器进行预测

分类问题包括 二分类类问题 和 多分类问题，我们可以将多分类问题转化为一对其余（One-vs-Test ）的二分类问题。我们将关注的类称为 正类（positive） 和 负类（negative）。

在分类过程中，预测类别与实际类别会有出入，出现 假阳性（False Positive） 和 假阴性（False Negative），也就是下表：

实际\预测	正	负	总计
正	TP	FN	P
负	FP	TN	N

我们定义分类器的 准确率（accuracy） 为正确分类的样本数与总样本数之比：

\[\text{accuracy}=\frac{TP+TN}{P+N}\]

但是准确率并不能完全反应模型的性能。比如：在 100 个短信中，有 1 个是垃圾短信，模型将所有的短信预测为非垃圾短信，准确率为 99%，但该模型是没有用的。所以一般不用准确率。

为进一步描述模型，我们定义 精确率（precision） 为预测的正类中实际正类的比例：

\[\text{precision}=\frac{TP}{TP+FP}\]

还定义 召回率（recall） （也叫灵敏度）为实际正类中，被预测为正例的比例：

\[\text{recall}=\frac{TP}{P}\]

精确率与召回率一般比较难做到同时都高，召回率升高时，预测为正类的数量会增加，假阳性的数量也会增加，反之亦然。为了综合这两个指标，我们绘制出 P-R曲线（PRC）（下图）：

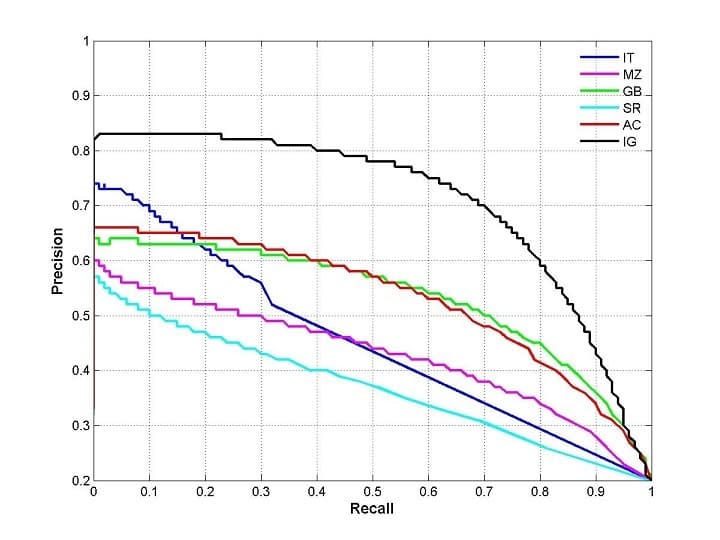
除了单独看 P值和 R值外，P-R 曲线所围成的面积 PRC-AUC（Area Under Curve） 越大，也能说明模型较好。

P-R 曲线的绘制方法如下：模型输出的是每个样本属于正类的概率，我们将所有概率排序，然后依次取每个概率作为阈值，规定大于阈值的为正类，这样就能计算出 P-R 曲线上的一点。取完所有的阈值后，就能得到 P-R 曲线。

但是以上依然不好分析，于是我们将精确率 $P$ 和召回率 $R$ 综合起来，定义 F 值 为两者的调和平均数：

\[F_{\beta-\text{score}} = \frac{1}{\frac{\beta^2}{(1+\beta^2)R}+\frac{1}{(1+\beta^2)P}}\\=\frac{(1+\beta^2)\cdot P \cdot R}{\beta^2 \cdot P + R}\]

$\beta$ 为重要程度，大于 0。当上式中的 $\beta$ 值取 $1$ 时，称为 $F_1$，表示两个同等重要。

另一种评价图像为：ROC（receiver operating characteristic）曲线，其横轴为虚惊率 FP rate（FP/N），纵轴为命中概率 TP rate（TP/T）

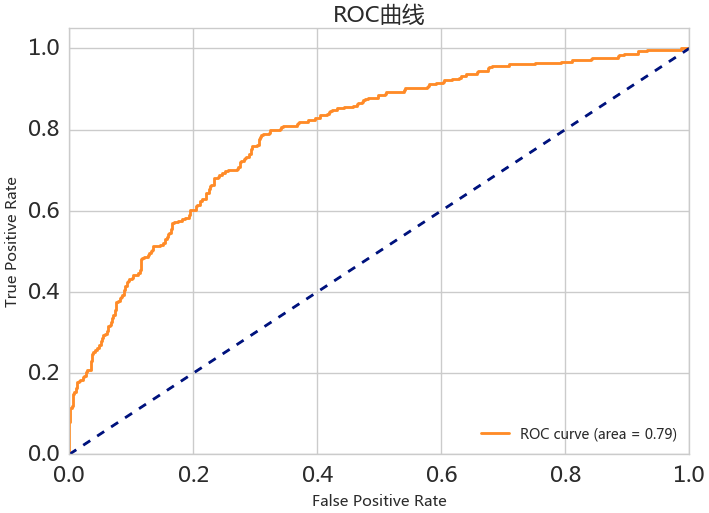
ROC 与 PRC 一样，也可根据所围成的面积 ROC-AUC 来评估模型的效果，面积越大，效果越好。同时 ROC 的画法和 PRC 一样。

评价分类模型好坏的重要指标ROC,PRC,KS

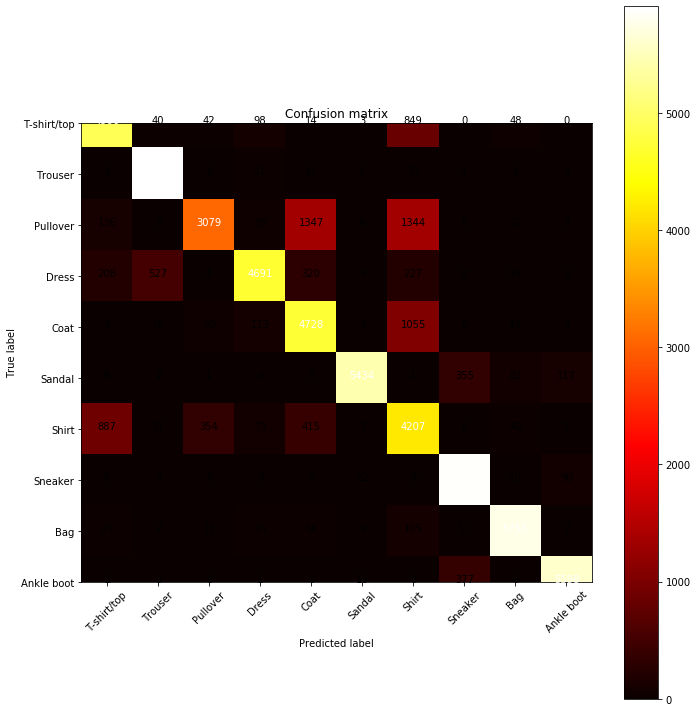
当然，啥都比不上可视化直观。比如下图就是某个分类模型的热度图（对角线上的是分类正确的，越热越多）：

上篇关于

下篇软件