4.1 介绍
在将图像处理算子之前,还了解直方图与直方图均衡化。这章会解释为什么对图像进行处理前需要先进行直方图均衡化,并展示了相应的代码。
4.2 直方图
直方图(histogram)是一张展示各级灰阶出现次数的柱状图。下面展示了一个简单的直方图。横轴是灰度的级数,从 0 到最大灰阶;每个竖条则表示该灰度在图中出现的次数。下图种可以看出峰值大概在 70 和 110 处,说明这些灰度比较常见。
* *
* * *
* ** ** * *
* * ** * *** * * * *
* * * *** * *** * * * * * *
*** ** ****** * **** ***** ******* **
* ****** ******** ***** ******* ********* ***
* ********************** **********************
************************************************
---------------------------------------------------
0 50 100 150 200 255
直方图有很多用途,比如它能表面该照片有没有拍好。下面这个直方图展示了一张没拍好的照片的直方图。可以看出灰度主要集中在较暗的一侧,说明这张照片太暗了,对比度不够明显。
** ** ***
** ** ***
*** ** ***
*** *** ***
* *** **** ***
* ********* ***
****************
-----------------------------------------------------
0 50 100 150 200 255
直方图可以帮助我们选择一个合适的物体检测阈值。图中的物体一般有相似的灰度。如果直方图中有多个阈值,那么有可能对应多个物体。如果图片太暗的话,人眼就很难分辨其中的物体,更不用说计算机了(比如 Figure 4.5)。

直方图均衡化
Figure 4.5 展示了一张低对比度的照片,图中白色的矩形是房车,周围的是道路、草地。它的直方图表明灰度主要集中在暗的一侧。实际上,图中还有一些树和灌木,但我们看不出来,因为它们的灰度与草地的灰度很接近。
要提高图片的对比图,就需要“直方图均衡化”。均衡化使得直方图中相近的峰值分散开来,使直方图变得均衡、平坦。这使得黑的“看起来”更黑,白的“看起来”更白。直方图均衡化并不是直接对直方图进行操作,而是利用直方图对图像进行调整。
为了更好的理解均衡化算法,我们来看看它的推导过程(详细的推到过程在 参考1.)。假设 $c$ 是一个低对比的图像,通过 $f$ 函数得到一个均衡的图像 $b$,即:
\[b(x,y)=f[c(x,y)] \tag{4.1}\]式 $(4.2)$ 是图中某个像素值为 $a$ 的概率密度函数。$p_c(a)$ 是在 ${\rm Area_1}$ 面积中的某个像素值为 $a$ 的概率,${\rm Area_1}$ 是面积,$H_c(a)$ 是 $c$ 的直方图。
\[p_c(a)=\frac{1}{ {\rm Area_1} } H_c(a) \tag{4.2}\]式 $(4.2)$ 式是像素值为 $a$ 的累积密度函数(cumulative-density function,cdf),是 $0$ 到 $a$ 的概率和:
\[P_c(a) = \frac{1}{ {\rm Area_1} } \sum_{i=0}^a H_c(a) \tag{4.3}\]$H_c(a)$ 是原图像 $c$ (对比度差的那个)的直方图,$H_b(f(a))$ 是新图像 $c$ (对比度好的那个)的直方图。由于 $b$ 的直方图比较平坦,所以有:$H_b(0)=H_b(1)=H_b(2)=\cdots$,即每个灰度出现的概率相同,出现的次数也相同,所以 $p_b(a)=1/D_m$,$D_m$ 是新图像 $b$ 中灰度的级数。又因为均衡化不会改变累计密度,所以 $P_b(f(a))=P_c(a)$,即:
\[\frac{1}{D_m} \times f(a) = \frac{1}{ {\rm Area_1} } \sum_{i=0}^a H_c(a)\\\]均衡化函数 $f$ 满足式 $(4.4)$
\[f(a)=\frac{D_m}{ {\rm Area_1} } \sum_{i=0}^a H_c(a) \tag{4.4}\]注意直方图均衡化会使得每个灰度的数值减小,虽然看上去有损失,但其实没有。
直方图均衡化的算法(见下)比上面的方程简单。
1. 计算直方图
循环图像的 i 行
循环图像的 j 列
k = input_image[i][j]
hist[k] = hist[k] + 1
结束 j 的循环
结束 i 的循环
2. 计算直方图的和
循环 i 级灰度
sum = sum + hist[i]
sum_of_hist[i] = sum
结束 i 循环
3. 将输入图像转化为输出图像
area = ROWS * COLS
Dm = 输出图像的灰度的级数
循环图像的 i 行
循环图像的 j 列
k = input_image[i][j]
out_image[i][j] = (Dm/area) * sum_of_hist[k]
结束 j 循环
结束 i 循环
代码实现
计算直方图
void calculate_histogram(unsigned char **image, unsigned long *histogram, int width, int height)
{
int i,j;
unsigned char k;
for(i=0; i<height; i++){
for(j=0; j<width; j++){
k = image[i][j];
histogram[k] = histogram[k] + 1;
}
}
} /* ends calculate_histogram */
绘制直方图
void draw_histogram(unsigned char **image, unsigned long *histogram, int width, int height, int maxval)
{
int max=0;
for(int i=0; i<maxval; i++)
if(histogram[i] > max)
max = histogram[i];
float y_scale = (height-1)*1.0/max;
float x_scale = (width-1)*1.0/maxval;
for(int i=0; i<maxval+1; i++)
{
int amount = histogram[i]*y_scale;
if(amount>0)
{
vline(image, i*x_scale, height-amount-1, height-1, 128);
}
}
hline(image, height-1, 0, width-1, 128);
}
void vline(unsigned char **image, int x, int ymin, int ymax, unsigned char color)
{
int i, j;
for(i=ymin; i<ymax; i++)
image[i][x] = color;
} /* ends vline */
void hline(unsigned char **image, int y, int xmin, int xmax, unsigned char color)
{
int i, j;
for(i=xmin; i<xmax; i++)
image[y][i] = color;
} /* ends hline */
效果如下:

直方图均衡化
void histogram_equalization(unsigned char **image,
unsigned long *histogram,
int gray_levels,
int new_grays,
int width,
int height)
{
int i, j, k;
unsigned long sum, sum_of_h[gray_levels];
double constant;
sum = 0;
for (i = 0; i < gray_levels; i++)
{
sum = sum + histogram[i];
sum_of_h[i] = sum;
}
/* constant = new # of gray levels div by area */
constant = (float)(new_grays) / (float)(height * width);
for (i = 0; i < height; i++)
{
for (j = 0; j < width; j++)
{
k = image[i][j];
image[i][j] = sum_of_h[k] * constant;
}
}
} /* ends histogram_equalization */
效果:
| Before | After |
|---|---|
 |
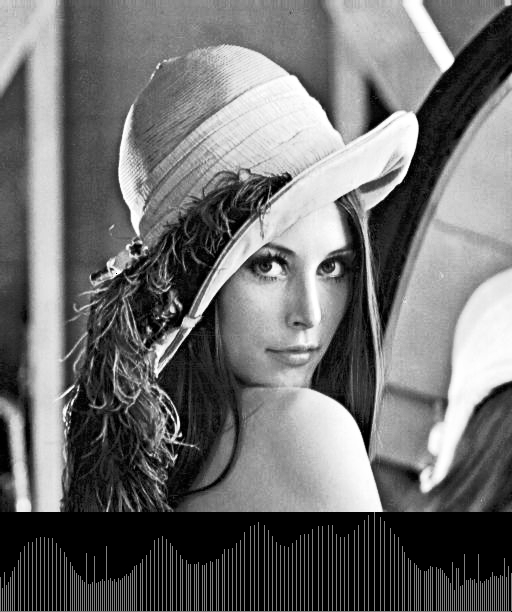 |
参考
- “Digital Image Processing,” Kenneth R. Castleman, Prentice-Hall, 1979.