一阶与二阶连续时间系统

$$ \newcommand{\dif}{\mathop{}\!\mathrm{d}} \newcommand{\xleftrightarrow}[1]{\stackrel{#1}{\longleftrightarrow}} \newcommand{\F}{\mathcal{F}} \newcommand{\ft}{\xleftrightarrow{\F}} $$

一阶连续时间系统

Bode图

一阶系统的微分方程往往表示为：

$$ \tau \frac{\dif y(t)}{\dif t}+y(t)=x(t) $$

（注：尽管更一般的方程应该是 $a \frac{\dif y(t)}{\dif t}+ b y(t)=c x(t)$，但由于 $b,c$ 只是线性增大了输入/输出的幅度，对探讨系统性质没影响，所以我们用上面的形式来讨论。）

其频率响应为：

$$ H(j\omega)=\frac{1}{1+j\omega \tau} $$

我们先考虑幅频特性。对其取对数，并在不同区间取近似：

$$ \begin{align} 20\lg |H(j\omega)|&=-10\lg [(\omega \tau)^2+1]\\ &\approx \begin{cases} -10 \lg 1=0 & \omega \ll 1/\tau\\ -10\lg 2=-3\;\mathrm{dB} & \omega=1/\tau\\ -10 \lg [(\omega \tau)^2]=-20 \lg (\omega \tau) & \omega \gg 1/\tau \end{cases} \end{align} $$

类似地，对相频特性也进行近似处理（不是很清楚第二条近似的数学推导，知道的同学在评论区写写）：

$$ \begin{align} \angle H(j\omega) &= -\arctan(\omega\tau)\\ &\approx \begin{cases} 0 & \omega \ll 0.1/\tau\\ -(\pi/4)[\lg(\omega\tau)+1] & 0.1/\tau \leq \omega\leq 10/\tau\\ -\pi/2 & \omega \geq 10/\tau \end{cases} \end{align} $$

作出 Bode图：

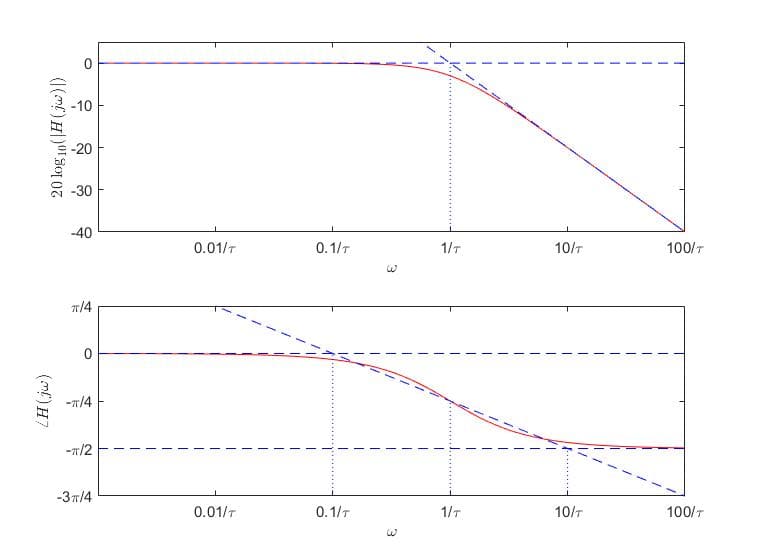
我们能从图中读出以下几点：

幅频曲线：
- 频率较低时，其增益为 0
- 频率较高时，按照每 10 倍频 20 dB 衰减
- 在 $1/\tau$ 处，两条近似直线相交，实际衰减幅度为 $-10\lg 2=-3\;\mathrm{dB}$。故该点又称为：转折频率（break frequency） 或 3dB点
相频曲线：
- 在转折频率上下十倍频范围内，$\angle H(j\omega)\sim\lg(\omega\tau)$ 图像近似线性下降

MATLAB代码

%matlab代码
tau=0.1;
omega=0:0.01:1000;
H=1./(1+i*omega*tau);

%幅频特性
subplot(2,1,1)
plot(log10(omega), 20*log10(abs(H)),'r');
hold on;
xticks(log10([0.01/tau, 0.1/tau 1/tau 10/tau 100/tau]))
xticklabels({'0.01/\tau','0.1/\tau','1/\tau','10/\tau','100/\tau'})
xlabel({'$\omega$'},'Interpreter','latex');
ylabel({'$20 \log_{10} (|H(j\omega)|)$'},'Interpreter','latex');

plot(log10(omega), 0.*omega,'b--');
plot(log10(omega), -20*log10(omega)-20*log10(tau),'b--');

plot([log10(1/tau),log10(1/tau)],[-40, 0],'b:')

axis([log10(omega(1)), log10(max(omega)),-40,5])

hold off

%相频特性
subplot(2,1,2)
plot(log10(omega), angle(H),'r');
hold on
xticks(log10([0.01/tau, 0.1/tau 1/tau 10/tau 100/tau]))
xticklabels({'0.01/\tau','0.1/\tau','1/\tau','10/\tau','100/\tau'})
yticks([-3*pi/4 -pi/2 -pi/4 0 pi/4 pi/2 3*pi/4])
yticklabels({'-3\pi/4','-\pi/2','-\pi/4','0','\pi/4','\pi/2','3\pi/4'})
xlabel({'$\omega$'},'Interpreter','latex');
ylabel({'$\angle H(j\omega)$'},'Interpreter','latex');

plot(log10(omega), 0.*omega,'b--');
plot(log10(omega), -(pi/4).*(log10(omega.*tau)+1),'b--');
plot(log10(omega), 0.*omega-pi/2,'b--')

plot([log10(0.1/tau),log10(0.1/tau)],[-3*pi/4, 0],'b:')
plot([log10(1/tau),log10(1/tau)],[-3*pi/4, -pi/4],'b:')
plot([log10(10/tau),log10(10/tau)],[-3*pi/4, -pi/2],'b:')

axis([log10(omega(1)), log10(max(omega)),-3*pi/4,pi/4])

hold off

冲激响应和阶跃响应

对应的单位冲激响应为：

$$ H(j\omega)=\frac{1}{1+j\omega \tau}\\ h(t)=\frac{1}{\tau}e^{-t/\tau} u(t) $$

对应的阶跃响应为：

$$ s(t)=h(t)*u(t)=[1-e^{-t/\tau}]u(t) $$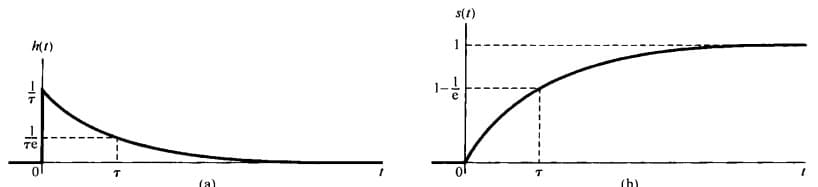

可以看出，$\tau$ 决定着冲激衰减与阶跃上升的速度，所以 $\tau$ 又称为时间常数。

最后，我们来看看不同频率的正弦信号经过一阶系统后的图像，加深对一阶系统的理解。从下面三个图可以看出，频率越高，信号输出的衰减幅度越大，同时相位差也越大。

输入	$\sin(t)$	$\sin(2t)$	$\sin(4t)$
图像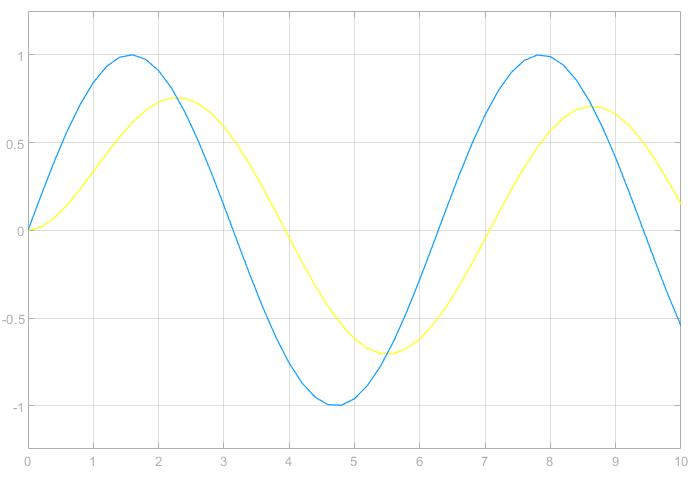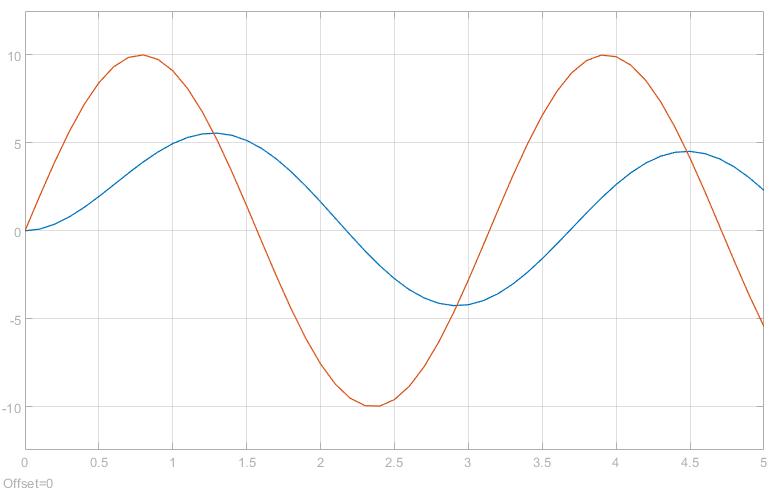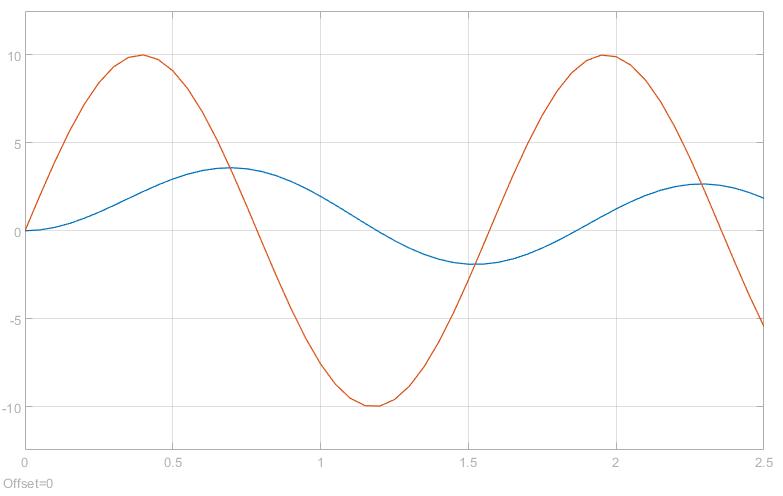

二阶连续时间系统

冲激响应与阶跃响应

二阶系统的微分方程可表示为：

$$ \frac{\dif^2 y(t)}{\dif t^2}+2 \zeta\omega_n \frac{\dif y(t)}{\dif t}+\omega_n^2 y(t)=\omega_n^2 x(t) $$

频率响应为：

$$ H(j\omega)=\frac{\omega_n^2}{(j\omega)^2+2\zeta \omega_n (j\omega)+\omega_n^2} $$

我们对分母进行多项式分解：

$$ H(j\omega)=\frac{\omega_n^2}{(j\omega-c_1)(j\omega-c_2)}\\ \begin{cases} c_1=\zeta\omega_n+\omega_n\sqrt{\zeta^2-1}\\ c_2=\zeta\omega_n-\omega_n\sqrt{\zeta^2-1} \end{cases} $$

对 $\sqrt{\zeta-1}$ 分情况讨论：

	$\zeta \neq 1$	$\zeta=1$
$c_1,c_2$	$c_1 \neq c_2$	$c_1=c_2=-\omega$
频率响应	$$H(j\omega)=\frac{M}{j\omega-c_1}-\frac{M}{j\omega-c_2}\\M=\frac{\omega_n}{2\sqrt{\zeta^2-1}}$$	$$H(j\omega)=\frac{\omega_n^2}{(j\omega+\omega_n)^2}$$
冲激响应	$h(t)=M[e^{c_1t}-e^{c_2t}]u(t)$	$h(t)=\omega_n^2 t e^{-\omega_n t}u(t)$

进一步将 $\zeta \neq 1$ 划分。如果 $0<\zeta<1$，那么冲激响应为：

$$ \begin{align} h(t) &= \frac{\omega_n e^{-\zeta\omega_n t}}{2 j \sqrt{1-\zeta^2}}\left\{ \exp\left[ j(\omega_n\sqrt{1-\zeta^2})t \right]-\exp\left[ -j(\omega_n\sqrt{1-\zeta^2})t \right]\right\}u(t)\\ &= \frac{\omega_n e^{-\zeta\omega_n t}}{j \sqrt{1-\zeta^2}} \sin(\omega_n t\sqrt{1-\zeta^2})u(t) \end{align} $$

从上式可以看出，这种情况下的冲激响应会有振荡（式中 $\sin$ 部分），当其幅度会衰减（式中 $e^{-\zeta\omega_n t}$ 部分）

如果 $\zeta>1$，这时是两个指数信号相减，不会有振荡。

综上，我们作出不同 $\zeta$ 值的图像（进行了适当缩放，y 轴是 $h(t)/\omega_n$）：

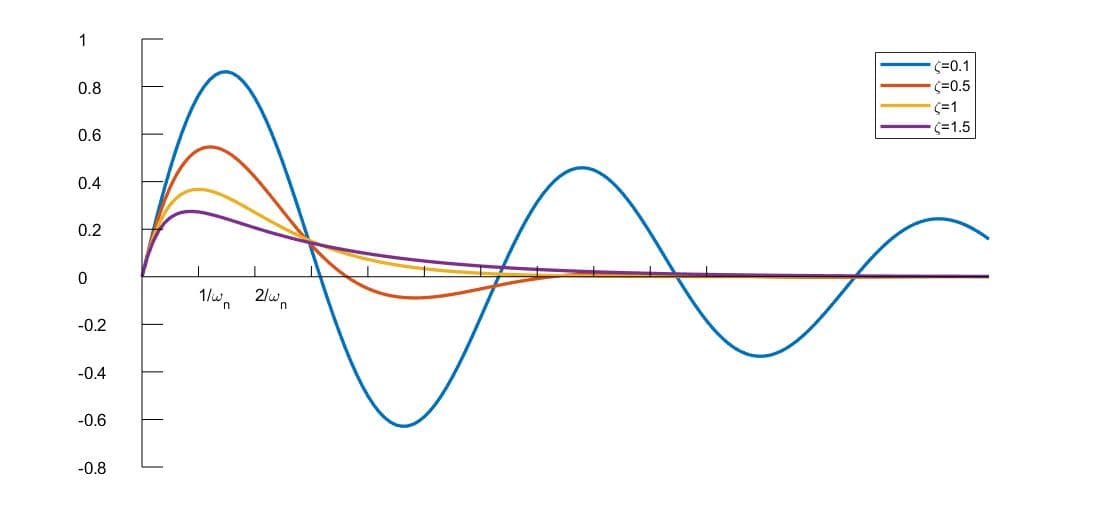
图中清楚地说明了 $\zeta$ 的影响，所以称 $\zeta$ 为 阻尼系数（damping ratio）。根据 $\zeta$ 的取值，将系统分为：

$0<\zeta<1$，欠阻尼（underdamped）
$\zeta=1$，临界阻尼（critically damped）
$\zeta>1$，过阻尼（overdamped）

$\omega_n$ 称为 无阻尼自然频率，$\omega_n$ 与 $\zeta$ 一同控制着时间尺度与幅度。$\omega_n$ 越大，则时间上越压缩，幅度上越大。在 $\zeta=0$ 时，振荡频率为 $\omega_n$。

最后补充一下，$\zeta<0$ 的情况与上面类似，也是分成三类振荡情况，只不过其幅度是增加而不是减小。

MATLAB代码

function secondOrderSystem(zeta,omegan)
    t=0:0.1/omegan:10/omegan;
    if zeta~=1
        c1=-zeta*omegan+omegan*sqrt(zeta^2-1);
        c2=-zeta*omegan-omegan*sqrt(zeta^2-1);
        h=omegan/(2*sqrt(zeta^2-1))*(exp(c1.*t)-exp(c2.*t));
    else
        h=omegan^2.*t.*exp(-omegan.*t);
    end
    plot(t.*omegan,h./omegan,'linewidth',2);
    %text=['\zeta=', num2str(zeta)];
    %legend(text);
end

hold on;
omegan=1;
secondOrderSystem(0.1,omegan);
secondOrderSystem(0.5,omegan);
secondOrderSystem(1,omegan);
secondOrderSystem(1.5,omegan);

xticks([1:10]/omegan)
xticklabels({'1/\omega_n','2/\omega_n'})
xlabel({'$t$'},'Interpreter','latex');
ylabel({'$h(t)/\omega_n$'},'Interpreter','latex');
xyplot %网上找的function，用于将 x 轴移到中间
legend('\zeta=0.1','\zeta=0.5','\zeta=1','\zeta=1.5')

对于阶跃响应，其特点与上面类似，也是分成：

$\zeta\neq1$	$$ s(t)=\left\{ 1+M\left[ \frac{e^{c_1t}}{c_1}-\frac{e^{c_2t}}{c_1} \right]\right\}u(t) $$
$\zeta=1$	$$ s(t)=\left[ 1-e^{-\omega_n t}-\omega_n t e^{-\omega_n t} \right] u(t) $$

其图像为（懒得再用matlab了）：

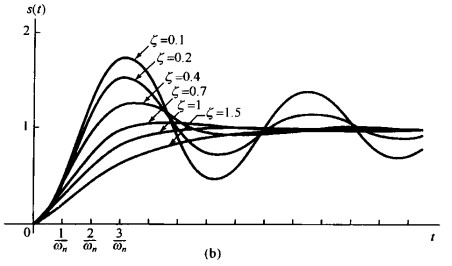
可以看到，欠阻尼情况下，阶跃响应有 超量（overshoot），即阶跃响应超过它的终止。

Bode图

频率响应为：

$$ \begin{align} H(j\omega)&=\frac{\omega_n^2}{(j\omega)^2+2\zeta \omega_n (j\omega)+\omega_n^2}\\ &=\frac{1}{(j\omega/\omega_n)^2+2\zeta (j\omega/\omega_n)+1}\\ &=\frac{1}{1-(\omega/\omega_n)^2+2\zeta (j\omega/\omega_n)} \end{align} $$

幅频特性：

$$ 20\lg |H(j\omega)|=-10\lg \left\{ \left[ 1- \left( \frac{\omega}{\omega_n}\right)^2 \right]^2+4\zeta^2 \left( \frac{\omega}{\omega_n} \right)^2 \right\} $$

若 $\omega\ll\omega_n$，则 $\omega/\omega_n\approx0$，$20\lg |H(j\omega)|=0$
若 $\omega\gg\omega_n$，则 $20\lg |H(j\omega)|\approx -10 \lg \left( \dfrac{\omega}{\omega_n} \right)^4=-40\lg \omega+40\lg \omega_n$

作出图像：

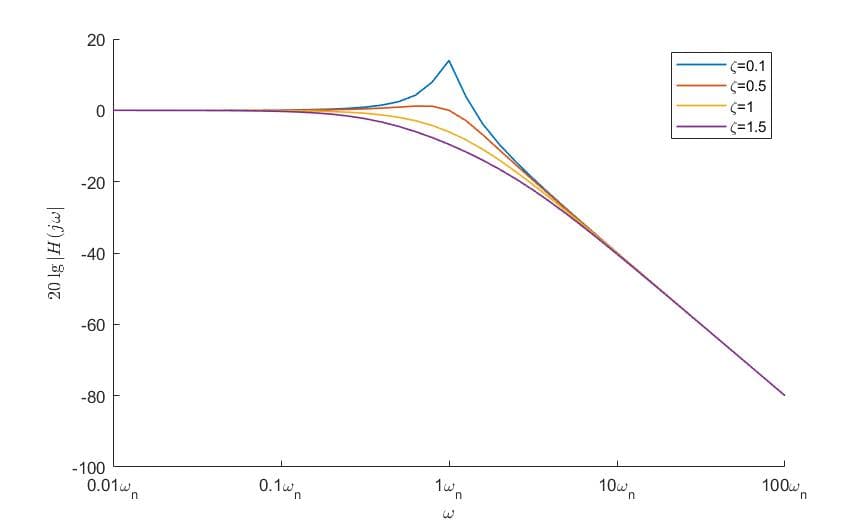
从图像中可以看出：

低频时，$20\lg\vert H(j\omega) \vert\approx 0 \rm{dB}$
高频时，以每十倍频 -40dB 速度下降
低频与高频交于 $\omega=\omega_n$，故 $\omega_n$ 称为二阶系统的转折频率
特殊地，注意到当 $\zeta$ 较小时，$\omega=\omega_n$ 处会有尖峰，我们用 品质因数 Q 来衡量峰值的尖锐程度。对于该二阶系统，$Q=1/(2\zeta)$

MATLAB代码

function secondOrderSystem(zeta,omegan)
    range=[-2:0.1:3]
    t=omegan.*10.^range;
    H=omegan^2./((i*omega).^2+2*zeta.*omegan.*i.*omega+omegan.^2)
    
    plot(range,20.*log10(abs(H)),'linewidth',1);
    %text=['\zeta=', num2str(zeta)];
    %legend(text);
end

hold on;
omegan=1;
secondOrderSystem(0.1,omegan);
secondOrderSystem(0.5,omegan);
secondOrderSystem(1,omegan);
secondOrderSystem(1.5,omegan);

xticks([-2:2])
xticklabels({'0.01\omega_n','0.1\omega_n','1\omega_n','10\omega_n','100\omega_n'})
xlabel({'$\omega$'},'Interpreter','latex');
ylabel({'$20\lg |H(j\omega|$'},'Interpreter','latex');
legend('\zeta=0.1','\zeta=0.5','\zeta=1','\zeta=1.5')

理想频率选择滤波器