离散时间傅里叶变换
$$ \begin{align*} \newcommand{\dif}{\mathop{}\!\mathrm{d}} \newcommand{\xleftrightarrow}[1]{\stackrel{#1}{\longleftrightarrow}} \end{align*} $$离散时间傅里叶变换
与连续傅里叶变换一样,我们同样通过傅里叶级数来推导出傅里叶变换。我们考虑一个信号 $\widetilde{x}[n]$ 具有如下性质:
- $\widetilde{x}[n]$ 是周期的,并且周期为 $2N$
- $N$ 很大
- $\widetilde{x}[n]$ 和 $x[n]$ 在 $-N< t< N$ 上具有相同值
那么,当 $N\rightarrow\infty$ 时,可以认为 $\widetilde{x}[n] = x[n]$。
我们先对 $\widetilde{x}[n]$ 进行傅里叶级数展开:
$$ \widetilde{x}[n]=\sum_{k=\langle -N, N \rangle} a_k e^{-jk(\pi/N)n}\\ a_k=\frac{1}{2N}\sum_{n=\langle -N, N \rangle} x[n] e^{-jk(\pi/N)n} $$从而有:
$$ \widetilde{x}[n]=\sum_{k=\langle -N, N \rangle} \left\{ \frac{1}{2N}\sum_{m=\langle -N, N \rangle} x[m] e^{jk(\pi/N)m} \right\} e^{jk(\pi/N)n} $$同时对 $k$ 进行如下替换:
$$ \Delta\omega=\frac{\pi}{N} \quad \omega_k=\frac{k\pi}{N} $$$\Delta\omega$ 表示相邻 $\omega_k$ 间的距离。代入傅里叶展式:
$$ \begin{align} \widetilde{x}[n]&=\sum_{\omega=\langle -\pi, \pi \rangle} \left\{ \frac{\Delta \omega}{2\pi}\sum_{m=\langle -N, N \rangle} x[m] e^{-j\omega_k m} \right\} e^{-j\omega_k n}\\ &=\frac{1}{2\pi} \sum_{\omega=\langle -\pi, \pi \rangle} \left\{ \sum_{m=\langle -N, N \rangle} x[m] e^{-j\omega_k m} \right\} e^{-j\omega_k n} \Delta \omega \end{align} $$当 $N\rightarrow \infty$ 时,$\Delta\omega\rightarrow 0$,$\omega$ 可以看作连续,积分区间变为无穷,即
$$ \begin{align} \widetilde{x}[n] &=\frac{1}{2\pi} \sum_{\omega=\langle -\pi, \pi \rangle} \left\{ \sum_{m=-\infty}^{+\infty} x[m] e^{-j\omega m} \right\} e^{-j\omega n} \Delta \omega\\ &=\frac{1}{2\pi} \sum_{\omega=\langle -\pi, \pi \rangle} X(e^{j\omega}) e^{-j\omega n} \Delta \omega \end{align} $$但是与连续时间傅里叶变换不同的是,$X(e^{j\omega})$ 和 $e^{-j\omega n}$ 都是以 $2\pi$ 为周期,所以 $X(e^{j\omega}) e^{-j\omega n}$ 以 $2\pi$ 为周期,所以我们只需要在任意 $2\pi$ 长的区间内积分:
$$ \widetilde{x}[n]=\frac{1}{2\pi} \int_{2\pi} X(e^{j\omega}) e^{j\omega n} \dif \omega $$
从上面,我们得到 离散傅里叶变换对:
$$ 综合公式:x[n]=\frac{1}{2\pi} \int_{2\pi} X(e^{j\omega}) e^{j\omega n} \dif \omega\\ 分析公式:X(e^{j\omega})=\sum_{n=-\infty}^{+\infty} x[n] e^{-j\omega n} $$我们这里用 $X(e^{j\omega})$ 是为了突出其周期性。
收敛问题
分析公式中的收敛问题就是级数的收敛问题,因此我们只需要满足 $\sum_{n=-\infty}^{+\infty} \vert x[n]\vert < \infty$ 或 $\sum_{n=-\infty}^{+\infty} \vert x[n]\vert^2 < \infty$,分析公式就收敛。(再次强调,这个依然只是充分不必要条件)
但对于综合公式,由于其积分区间有限,所以不会有收敛问题。
常见离散傅里叶变换
指数阶跃
考虑信号 $x[n]=a^n u[n]$,$\vert a \vert< 1$,对应的傅里叶变换为:
$$ X(e^{j\omega})=\sum_{n=0}^{+\infty} a^n u[n]e^{-j\omega n}=\sum_{n=0}^{+\infty} (ae^{-j\omega})^n=\frac{1}{1-ae^{-j\omega}} $$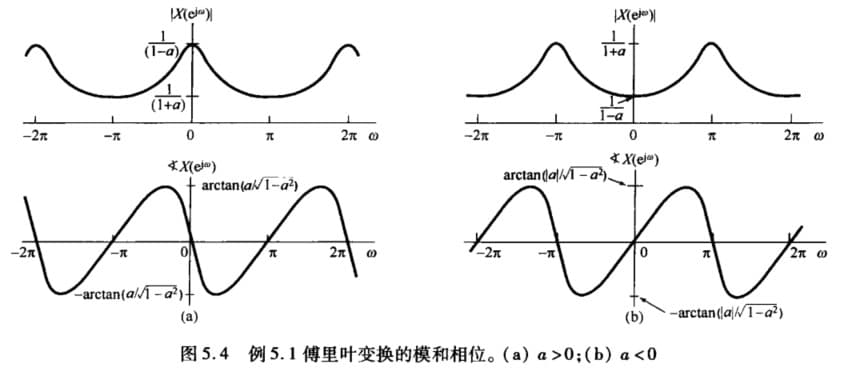
矩形脉冲
$$ x[n]= \begin{cases} 1 & |n|\leq N_1\\ 0 & |n|>N_1 \end{cases} $$$$ X(e^{j\omega})=\sum_{n=-N_1}^{N_1} e^{-j\omega n}=\frac{\sin\omega (N_1+\frac{1}{2})}{\sin(\omega/2)} $$补充一下计算过程(点击展开)
阶跃信号
$$ u[n]= \begin{cases} 1 & n\geq 0\\ 0 & n< 0 \end{cases}\\ X(e^{j\omega})=\frac{1}{1-e^{-j\omega}}+\sum_{k=-\infty}^{+\infty} \pi \delta(\omega - 2\pi k) $$补充一下计算过程(点击展开)
对于 $f[n]$,根据下面的离散周期信号 DTFT,求得:
对于 $g[n]$,可以借助 $\delta[n]$ 求 DFTF:
综上,可以得到:
离散周期信号 DTFT
离散时间周期信号的傅里叶级数:
$$ x[n]=\sum_{k=\langle N \rangle} a_k e^{j\omega_0 kn}, \; \omega_0=\frac{2\pi}{N} $$如果我们能将基本信号 $e^{j\omega_0 n}$ 的傅里叶变换求出来,那么就能通过线性性求得离散周期信号的 DTFT(Discrete Time Fourier Transform)。但这个信号并非绝对可积或能量有限,所以不能通过分析公式求(反正我是没求出来)。我们先猜测其傅里叶变换为冲激函数:
$$ X(e^{j\omega})=2\pi\delta(\omega-\omega_0)\\ x[n]=\frac{1}{2\pi} \int_{2\pi} \delta(\omega-\omega_0) e^{j\omega n} \dif \omega\\= \begin{cases} e^{j\omega_0 n} & \omega_0在 2\pi区间内\\ 0 & \omega_0不在 2\pi区间内 \end{cases} $$为了使 $X(e^{j\omega})$ 在任何 $2\pi$ 区间上的积分都等于 $e^{j\omega_0 n}$,我们对其进行周期性平移:
$$ X(e^{j\omega})=\sum_{l=-\infty}^{+\infty} 2\pi\delta(\omega-\omega_0-2\pi l) $$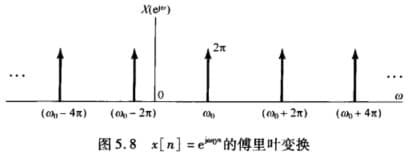
那么根据线性性,离散周期信号 DTFT 为:
$$ \begin{align} X(e^{j\omega})&=\sum_{k=-\infty}^{+\infty} 2\pi a_k \delta(\omega-k\omega_0-2\pi l)\\ &=\sum_{k=-\infty}^{+\infty} 2\pi a_k \delta(\omega-\frac{2\pi k}{N}-2\pi l)\\ &=\sum_{k=-\infty}^{+\infty} 2\pi a_k \delta(\omega-\frac{2\pi (k+Nl)}{N})\\ &=\sum_{k=-\infty}^{+\infty} 2\pi a_k \delta(\omega-\frac{2\pi k}{N}) \quad 重新取k \end{align} $$