卷积和与卷积积分
$$\begin{align*}\newcommand{\dif}{\mathop{}\!\mathrm{d}}\end{align*}$$引入
卷积和
在说什么是卷积之前,先说说为什么要“卷积”。我们知道 LTI系统,也就是线性时不变系统有两个特征:线性+时不变,也就是说我们对输入做加、减、乘、除和时移,输出也会同样地做相同运算。那么会不会有一种“元信号”,能够通过运算表示出其他信号?这样,我们只要知道元信号对应的输出,再进行运算,就能知道任何信号的输出。也就是:
$$ 元信号 \rightarrow 输出\\ \quad\Downarrow \;变换\;\Downarrow\\ 任何信号 \rightarrow 输出 $$那么“元信号”到底是什么?对于离散的情况,我们很容易想到 单位脉冲信号:
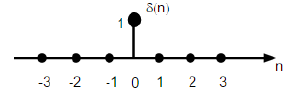
显然,我们可以用单位脉冲信号表示任何离散信号:
$$ \begin{align} x[n]&=\cdots+\delta[n+1] x[n]+\delta[n]x[n]+\delta[n-1]x[n]+\cdots\\ &=\cdots+\delta[n]x[n-1]+\delta[n]x[n]+\delta[n]x[n+1]+\cdots \end{align} $$那么,若我们知道的单位脉冲信号的输出:$\delta[n]\rightarrow h[n]$
由于
- 时不变性质:$\delta[n-k]\rightarrow h[n-k]$
- 线性性:$x[k]\delta[n-k]\rightarrow x[k]h[n-k]$
叠加可得:
$$ \begin{align} \sum_{k=-\infty}^{+\infty} x[k]\delta[n-k]&\rightarrow\sum_{k=-\infty}^{+\infty} x[k]h[n-k]\\ \Downarrow&\\ x[n]&\rightarrow y[n] \end{align} $$可见,如果我们知道离散时间线性时不变系统的单位脉冲响应 $h[n]$,则我们可以算出任意信号 $x[n]$ 的响应 $y[n]=\sum_{k=-\infty}^{+\infty} x[k]h[n-k]$
我们把这种计算称为卷积和(convolution sum),记作:$x[n]*h[n]=\sum_{k=-\infty}^{+\infty} x[k]h[n-k]$
卷积积分
对于连续的情况,当我们仿照上面来思考时,我们所遇到的第一个难题是:冲激函数可以表示其他函数吗?我们知道冲激函数的定义为:
$$ \delta(t) = \begin{cases} 0, \; t \ne 0\\ \infty, \; t=0 \end{cases} $$但这个定义是极度不准确的,因为缺少了一部分:
$$ \int_{-\infty}^\infty \delta(t) \dif t= 1 \rightarrow \text{强度为1} $$我们不能只看到 $\infty$,还要看到 $\int\dif t$,这两者共同作用下,有:
$$ \int_{-\infty}^\infty x(t)\delta(t) \dif t= \int_{-\infty}^\infty x(0)\delta(t) \dif t=x(0) $$$$ x(t)=\int_{-\infty}^{+\infty}x(\tau)\delta(t-\tau)\dif\tau\\ $$假如我们已知系统对冲激信号的响应:$\delta(t)\rightarrow y_\delta(t)$
同理,由时不变性质:$\delta(t-\tau) \rightarrow y_\delta(t-\tau)$
由齐次性:$x(\tau)\delta(t-\tau) \rightarrow x(\tau)y_\delta(t-\tau)$
叠加可得:$\int_{-\infty}^{+\infty} x(\tau)\delta(t-\tau) \dif \tau \rightarrow \int_{-\infty}^{+\infty} x(\tau)y_\delta(t-\tau) \dif \tau$
从而对于信号 $x(t)$ 有 $x(t) \rightarrow \int_{-\infty}^{+\infty} x(\tau)\delta(t-\tau) \dif \tau$,我们称之为 卷积积分(convolution integral)。
杜阿美积分(扩展)
假如我们已知线性时不变系统对阶跃信号的响应:$u(t)\rightarrow y_u(t)$
由时不变性质:$u(t-\tau) \rightarrow y_u(t-\tau)$
由齐次性:$x'(\tau)u(t-\tau) \rightarrow x'(\tau)y_u(t-\tau)$
从而我们可以进行叠加:$\int_{0^+}^t e'(\tau)u(t-\tau) \dif \tau \rightarrow \int_{0^+}^t e'(\tau)y_u(t-\tau) \dif \tau$
从而对于信号 $x(t)$ 有:
$$ \begin{align} x(t) &= x(0)u(t) + \int_{0^+}^t x'(\tau)u(t-\tau) \dif \tau \\ \downarrow \;\;&\\ y_x(t) &= x(0)y_u(t) + \int_{0^+}^t e'(\tau)y_u(t-\tau) \dif \tau \end{align} $$因此只要知道系统对阶跃信号的响应,就可以求出系统对任意连续可导信号的响应。我们将 $x(t)\rightarrow e(0)y_u(t) + \int_{0^+}^t e'(\tau)y_u(t-\tau) \dif \tau$ 称为杜阿美积分(Duhamel’s Integral)
杜阿美积分的另一种形式为为:
$$ x(t)\rightarrow x(0)y_u(t) + \int_{0^+}^t x'(t-\tau)y_u(\tau) \dif \tau $$由于很多信号是很难求导甚至不可求导的,所以杜阿美积分很难求。所以卷积积分比杜阿美积分更好用。
卷积
- 卷积
- f, g 的卷积记为 $f*g$
- 连续定义为:$(f*g)(t)=\int_{-\infty}^{\infty} f(\tau)g(t-\tau) \dif \tau$
- 离散定义为:$(f*g)[n]=\sum_{\tau=-\infty}^\infty f[\tau]g[n-\tau]$
以连续定义为例,我们观察等号两边的自变量,会发现:$(x)=(\tau)+(x-\tau)$。如果将右边改写为:$x=a(\tau)+b(\tau)$,令 $x$ 变化,则相当于(图中 x=a,y=b):
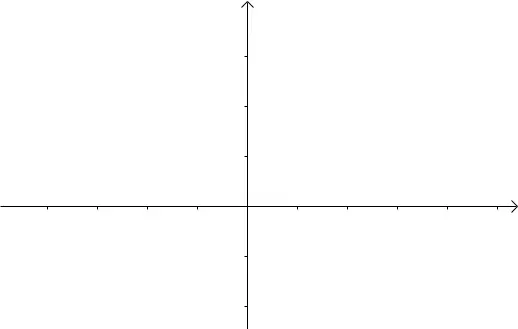
如果我们单独选取其中的一条线,比如 $1=a+b$,线上每个点对应一个 $f(a)g(b)$,我们把这条线卷起来(积分),就得到“卷积”。所以我认为,“积”代表的是乘积,“卷”代表的是相加。
卷积的性质
卷积具有如下性质:
- 交换律 Commutativity:$f_1*f_2=f_2\*f_1$
结合律 Associativity:$(f_1*f_2)\*f_3=f_1\*(f_2\*f_3)$
分配律 Distributivity:$f_1*(f_2+f_3)=f_1\*f_2+f_1\*f_3$
Duration:Let the signals $f_1(t)$ and $f_2(t)$ have durations, respectively, defined by the time intervals $[t_1, T_1]$ and $[t_2,T_2]$ then
$$ f(t)=f_1(t)*f_2(t)= \begin{cases} 0 & t\leq t_1+t_2\\ \int_{(t_1+t_2)/2}^{(T_1+T_2)/2} f_1(\tau)f_2(t-\tau)\dif \tau & t_1+t_2\leq t\leq T_1+T_2\\ 0 & t\geq T_1+T_2\\ \end{cases} $$
- 时移 Time Shifting:Let $f(t)=f_1(t)*f_2(t)$. Then, convolutions of shifted signals are given by $ f(t-\sigma_1)=f_1(t-\sigma_1)*f_2(t)\\ f(t-\sigma_2)=f_1(t)*f_2(t-\sigma_2)\\ f(t-\sigma_1-\sigma_2)=f_1(t-\sigma_1)*f_2(t-\sigma_2) $
- 微分:$\frac{\dif}{\dif t} [f(t)\*g(t)]=\left[ \frac{\dif}{\dif t} f(t) \right]\*g(t)$ $=f(t)\* \left[ \frac{\dif}{\dif t} g(t) \right]$(不是加)
- 积分:$\int_{-\infty}^t f(\tau)*g(\tau) \dif \tau$ $=\int_{-\infty}^t f(\tau)\dif \tau * g(\tau)$ $=f(\tau)\*\int_{-\infty}^t g(\tau)\dif \tau $(不是加)
- 多重微积分:$f(t)^{(m)}\*g(t)^{(n)}=[f(t)\*g(t)]^{(m+n)}$
利用以上性质,可以让求解卷积变得更简单。比如:
- 利用交换律,使得简单地函数处在 $f(t-\tau)$ 的位置。(合理选择作为“平移”的函数)
Tip
例题:计算 $e^{-t}u(t)$ 和 $\sin(t)$ 的卷积
答案
Note
若采用第一个等式:
若采用第二个等式:
- 利用微分、积分化简折线形的信号
Tip
例题:求下面两个信号的卷积。
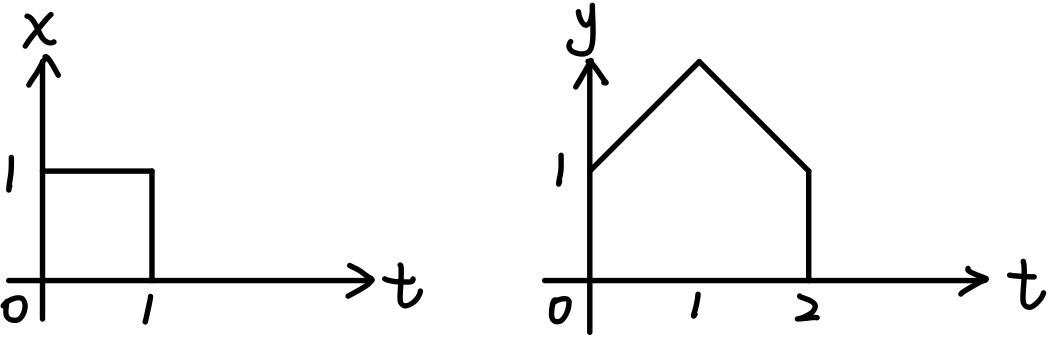
Note
解:这题直接用定义算有点复杂,我们可以先对 $y$ 进行微分:
再根据积分性质:
先计算 $x(t)$ 和 $\frac{\dif y(t)}{\dif t}$ 的卷积,然后对结果积分,就求得 $x(t)*y(t)$。计算很简单,这里就不写了。
Caution
注:细心的同学可能会发现,如果将 $y(t)$ 向上平移一个单位,微分后再和 $x(t)$ 卷积、积分,得到的结果和原题是一样的。这是因为,上面的方法要求两个信号必须都是有始信号。至于为什么要求是有始信号,可以看这篇论文 关于利用微分与积分性质计算卷积的条件,简单来说就是要满足 $f(t)=\int_{-\infty}^t f'(t)\dif t=f(t)-f(-\infty)$
关于积分、微分性质的练习题,可以看 用卷积的积分、微分性质,计算卷积