系统

$$\begin{align*}\newcommand{\dif}{\mathop{}\!\mathrm{d}}\end{align*}$$

系统的分类与性质

连续时间与离散时间系统

连续时间系统（continuous-time system）

输入和输出都是连续时间信号称为连续时间系统，可以用以下符号表示系统的输入-输出关系：

$$ x(t) \rightarrow y(t) $$

离散时间系统（discrete-time system）

输入和输出都是离散时间信号称为离散时间系统，可以用以下符号表示系统的输入-输出关系：

$$ x[n] \rightarrow y[n] $$

系统的互联

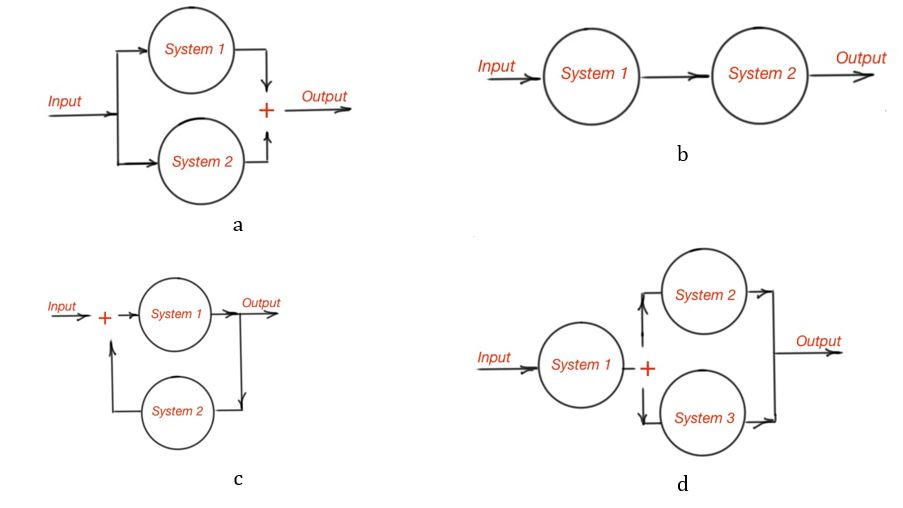
系统有多种组合方式：

1. 串联（series interconnnection）/级联（cascade interconnection） 前一个输出是后一个输入
2. 并联（parallel interconnection） 同输入，合输出
3. 混联，又串又并
4. 反馈互联（feedback interconnection） 后一个输出是前一个输入

系统的基本性质

记忆性

无记忆系统（memory system）

对于自变量的每一个值，一个系统的输出仅仅取决于该时刻的输入，则称该系统为无记忆（memoryless）系统，反之为记忆系统

比如：恒等系统（identity system）y=x 是无记忆系统，累加器（accumulator）y=y[n-1]+n 是记忆系统。

可逆性

可逆系统（invertible system）

如果输入与输出时一一对应的，则称该系统是可逆的

如果一个可逆系统与另一个系统级联后构成一个恒等系统，则称后者是前者的 逆系统（inverse system）

因果性

因果系统（causal）

如果一个系统在任何时刻的输出只取决于现在或过去的输出，则该系统就称为因果系统，也称为不可预测的系统，因为系统的输出无法预测未来的输入值。

这个可能有点莫名奇妙，我们来看一个例子：$y(t)=x(t+1)$ 当 $t=1$ 时，$y(1)$ 取决于 $x(2)$，也就是取决于输入 $x(t)$ 在 $t=2$ 的值，则这个显然与当前、之前的输入无因果关系，也就不是因果系统。

因果系统的判断其实很简单，就是看输入 $x(t+t_0)$ 中 $t_0$ 大于还是小于0，如果大于0，则系统就不是因果系统，比如 $x(t+1)$ 显然是未来的量；以及 $x(at)$ 如果 $a\neq 1$，则 $x(t)$ 也不是因果的。

稳定性

稳定系统（stable）

如果一个系统当输入有界时，产生的输出也是有界的，则是稳定系统（stable），否则是不稳定系统（unstable）

移不变性/时不变性

移不变系统（shift-invariant）

若系统的特性和行为不随时间改变而改变，则是 移不变系统，也叫 时不变系统（time-invariant）

用数学表示为：$x_1(t)=x(t-t_0)\rightarrow y_1(t)=y(t-t_0)$

下面来说说我的理解。时不变系统其实蛮直观的，就是输入与输出的时移要同步，比如你输入时移了1秒，那你输出也要时移1s，不能说时移个2、3秒。这里我们要区分“输入时移”与“输出时移”。输入时移指的是对于 $x(t)$里面的部分要加/减一个数，也就是对原时间轴进行移动；而输出时移是指 $y(t)$ 里面的部分加/减一个数，也就是对函数整个移动。

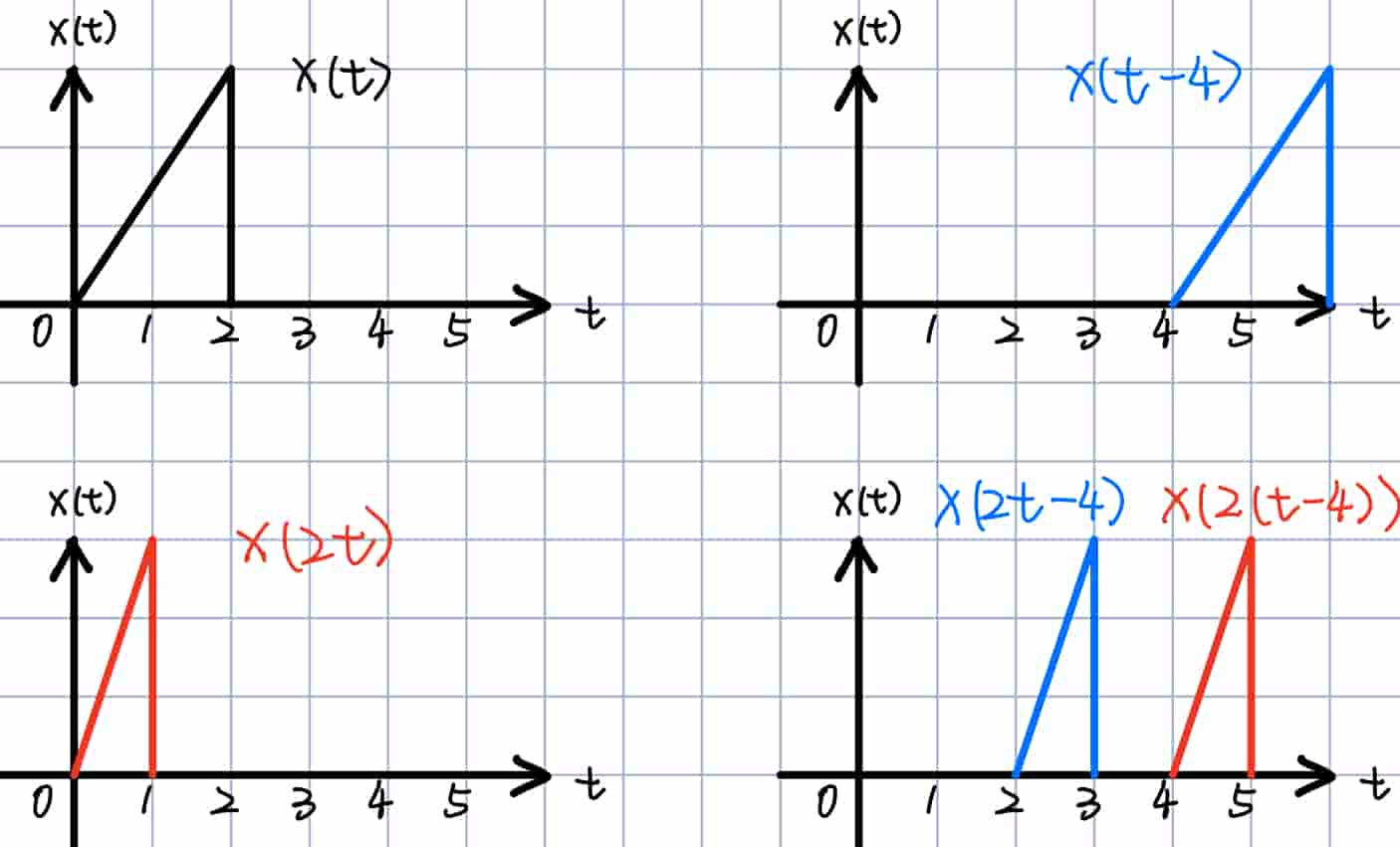
比如，输入信号为 $x(t)$，系统输出为 $y(t)=x(2t)$ ，现在我们有 $x_1(2t-4)$ 和 $x_2(2(t-4))$，从下图中，很明显发现 $x_1(2t-4)$ 是输入时移，$x_2(2(t-4))$ 是输出时移。

为了方便理解，我提供一个现实解释：$2t$ 相当于我们现在以 2倍速播放音乐；而输入时移相当于我们先跳到音乐4分分钟的位置，再以两倍速播放音乐；输出时移相当于以两倍速播放4分钟。这两种时移的结果不同，所以是时变系统。

做题时判断是否是时不变系统的步骤：

$$ \text{设输入为} x_1(t) \text{, 对应输出为} y_1(t)\\ \text{设输入为} x_2(t) \text{, 对应输出为} y_2(t)\\ \text{则当} x_2(t)=x_1(t-t_0)\text{时},\; y_2(t)=y_1(t-t_0) $$

扩展阅读：知乎理解离散时不变系统的含义

线性性

线性系统

满足可加性¹（additivity）和比例性²（scaling）/齐次性（homogeneity）的系统称为线性系统

用数学定义为：$ax_1(t)+bx_2(t)\rightarrow ay_1(t)+by_2(t)$ 或 $ax_1[n]+bx_2[n]\rightarrow ay_1[n]+by_2[n]$

我们可以通过以下方法来理解/判断线性系统：

1. 先输入系统再线性组合：$y_1(t)=T[x_1(t)], y_2(t)=T[x_2(t)]$ 得到$ay_1(t)+by_2(t)=aT[x_1(t)]+bT[x_2(t)]$
2. 先经过线性组合再输入系统：$x_3(t)=ax_1(t)+bx_2(t)$ 得到 $T[x_3(t)]$
3. 比较上两式是否相同，是则为线性系统

$$y[n]=x[n^2]$$

[!NOTE] 答案： $$

y_1[n]=x_1[n^2]=T[x_1[n]],;y_2[n]=x_2[n^2]=T[x_2[n]]\ T[a_1x_1[n]+a_2x_2[n]] \begin{align} &=ax_1[n^2]+bx_2[n^2]\ &=ay_1[n]+by_2[n]\ &=aT[x_1[n]]+bT[x_2[n]] \end{align} $$

---

有一种系统，其基本形式为 $r(t)=e(t)+C$, $C\neq 0$，这显然不是线性系统，但这种系统在工程中很常见，我们定义这种系统为 增量线性系统（incrementally linear system），其基本特征为：激励和响应的增量满足齐次性和叠加性，即

$$ a\Delta e_1(t)+b\Delta e_2(t)\rightarrow a\Delta r_1(t)+b\Delta r_2(t) $$

或者说，我们将系统响应分为零输入响应³ $r(t)=C$，和零状态响应⁴ $r(t)=C$，只要零状态响应满足线性条件即可。

系统的表示方法

• 输入输出方程：$y(t)=f(x(t))$，有些书上也写成 $r(t)=f(e(t))$。题目经常给出常系数微分方程，要你求输入输出方程。
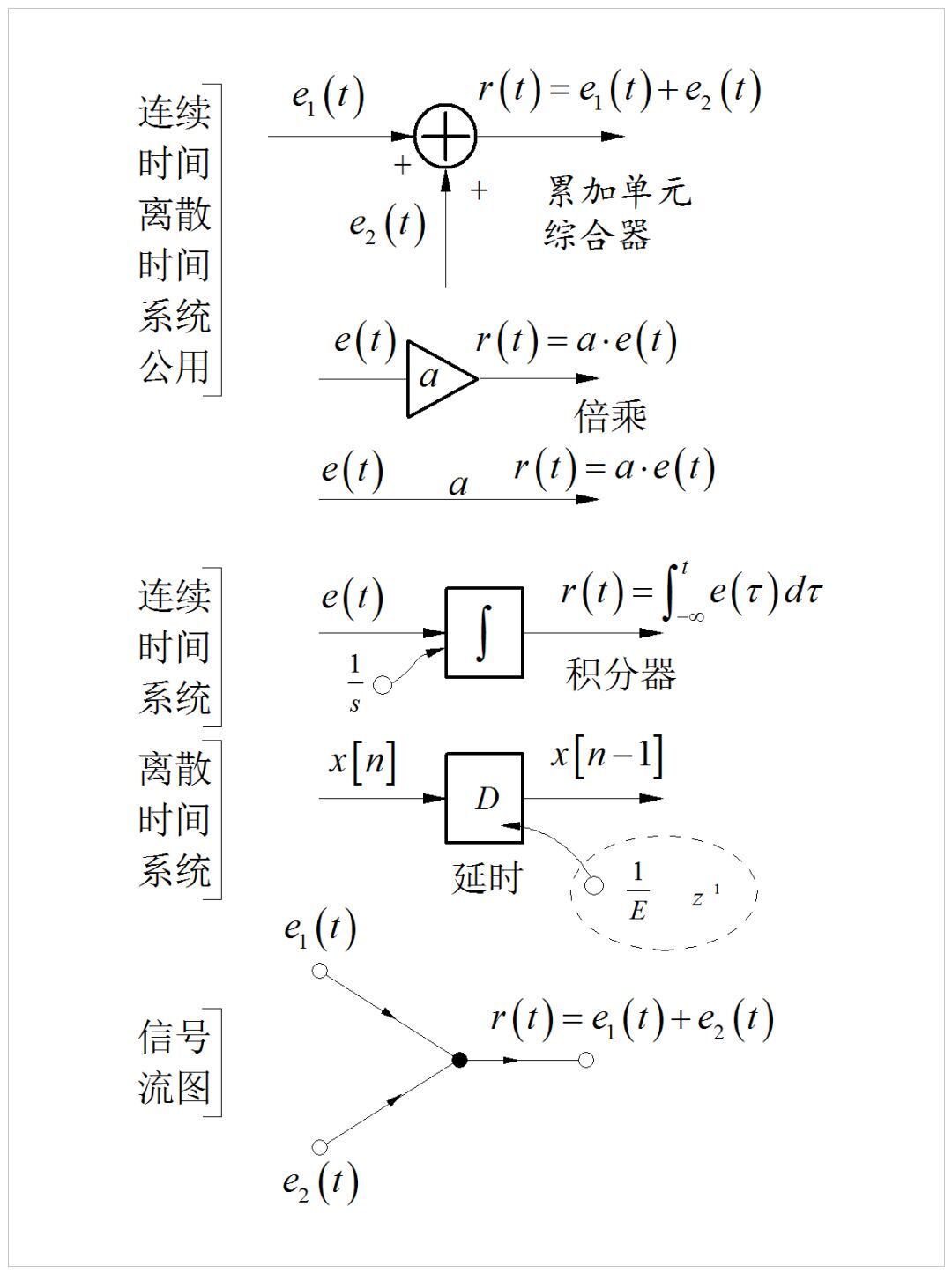
• 框图：利用基本的功能部件（标量乘法器、乘法器、加法器、积分器、微分器等）的组合来表示复杂的系统

下面是一些基本部件的框图。

信号与系统的系统仿真框图怎么画？

系统的研究

对系统的研究包括：

1. 已知系统特性和激励，求输出 —— 分析；
2. 已知系统输入和输出，求特性 —— 识别；
3. 已知输入和预期输出，求系统 —— 设计；

系统分析的步骤

1. 建立数学模型：把系统的工作表达为抽象的数学模型；
2. 分析：解方程，通过数学推导得到结果；
3. 物理解释：将结果从物理意义上进行解释，便于工程应用。

这门课程主要学的就是如何分析。

系统分析的方法

1. 时域法：直观但求解困难
   1. 经典法
   2. 算子法——第2章
2. 变换域法：求解容易但需要作两次变换
   1. 频域法——第4、5、6、7章
   2. 复频域法——第8、9章
3. 状态方程法：