系列
半导体器件
Bipolar Transistors

Bipolar Transistors

$$ \begin{align*} \newcommand{\dif}{\mathop{}\!\mathrm{d}} \newcommand{\belowarrow}[1]{\mathop{#1}\limits_{\uparrow}} \newcommand{\bd}{\boldsymbol} \newcommand{\L}{\mathscr{L}} \end{align*} $$

8.1 Introduction to the BJT

bipolar junction transistor or BJT 是 1948 年由贝尔实验室发明的。尽管现在 IC 里面大部分都是低功耗的 MOS 管，但由于 BJT 具有高速、低噪、高输出功率的优点，所以一些放大器还是用 BJT.

BJT 的结构：

  • NPN
    • heavily doped N+ emitter 射极
    • P-type base 基极
    • N-type collector 集电极
  • PNP
    • heavily doped P+ emitter 射极
    • N-type base 基极
    • P-type collector 集电极

由于电子的 mobility 比空穴高，所以 NPN 的 transconductance 和 speed 比 PNP 高，因此 NPN 比 PNP 更常用。

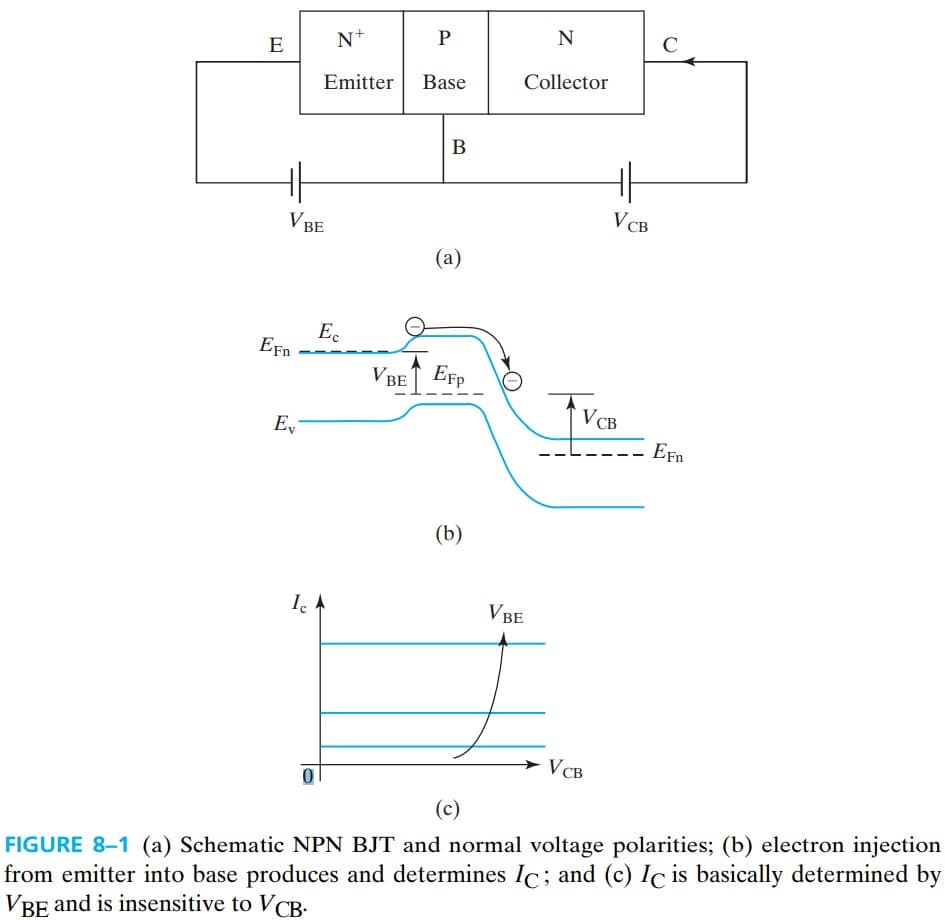
当 $V_{BE}$ 正偏，$V_{CB}$ 反偏时，电子从射极注入，然后在基极扩散，然后受电场作用扫到集电极，从而产生集电极电流 $I_C$. 注入一定的电子，扩散过程中复合率一定，剩下的全跑到集电极，$V_{CB}$ 只起到一个收集作用，所以 $I_C$ 与 $V_{CB}$ 的大小无关，只要 $V_{CB}$ 反偏即可。$I_{C}$ 只与电子注入的多少有关，而根据二极管的公式，电子注入的多少又与 $e^{qV_{BE}/kT}$ 成正比，所以最终可以得到 Fig. 8-1c.

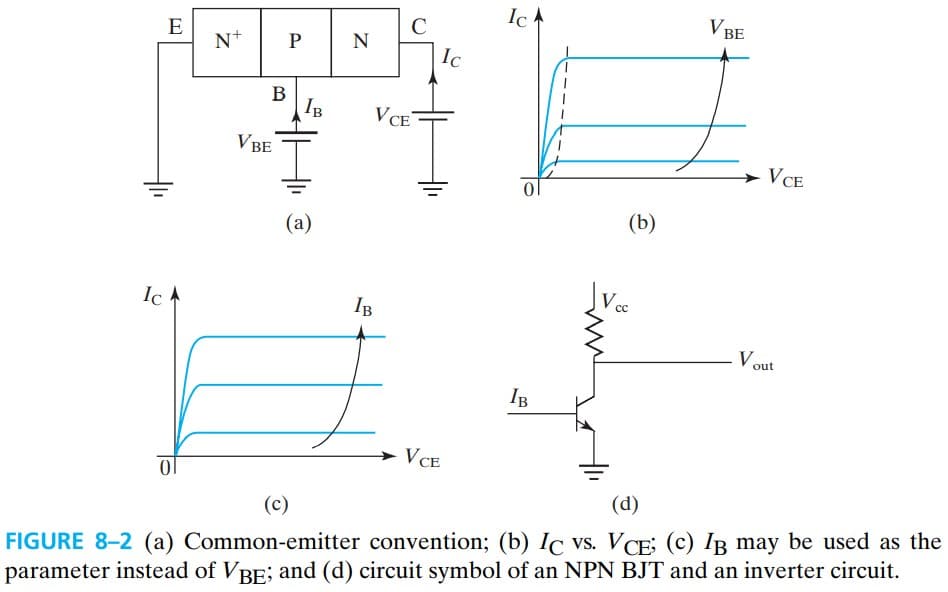
实际中基极接地，基极、集电极电压用对地电压来表示，也就是 $V_{BE},V_{CE}$ ，上图中的 Fig 8-1c 就改成了下图中的 Fig 8-2 b，注意到图中虚线前面部分对应着 $V_{CB}$ 反偏，因为 $V_{CE}=V_{BE}+V_{CE}$，$V_{BE}$ 一般大于 $0.3V$ （锗二极管的导通电压）因此 $V_{CE}<0.3V$ 时，对应着虚线前面那部分。

由于存在 parasitic IR drop（寄生的压降），比较难测量实际加在 BE 上的电压，所以用 $I_B$ 来代替，而 $I_B$ 与 $e^{qV_{BE}/kT}$ 成正比，同时，$I_C$ 也与 $e^{qV_{BE}/kT}$ 成正比（二极管），所以 $I_C$ 正比于 $I_B$.

8.2 Collector Current

上面说过，Electron are injected from emitter to base, and diffuse across the base, and get swept into the collector. This produces a collect current. 而在 PN 结的分析中，我们知道 minority-carrier current is dominated by diffusion current，即：$J_n = q D_n \dfrac{\dif x}{\dif x}$，因此我们可以认为 $I_C$ 主要是 diffusion current：

$$ \begin{aligned} I_C &= A_E J_n = \left|A_E q D_B \frac{\dif n}{\dif x}\right|\\ \end{aligned} $$

为了求出 $n$ 与 $x$ 的关系式，我们用 electron diffusion equation （就是 4.7 中的 current continuity equation）对基极进行分析：

$$ \frac{\dif^2 n'}{\dif x^2} = \frac{n'}{L_B^2}\\ 其中，L_B \equiv \sqrt{D_B \tau_B} $$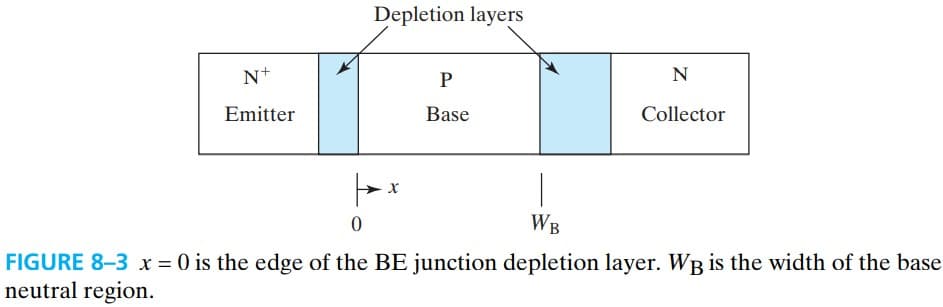

我们规定 $x=0$ 为靠近射级一端，从而 boundary conditions 为：

$$ 正偏 n'(0) = n_{B0} (e^{qV_{BE}/KT}-1) \\ 反偏 n'(W_B) = n_{B0} (e^{qV_{BC}/KT}-1) \approx -n_{B0} \approx 0 $$

$n_{B0}$ 是原本的少子浓度，即 $n_{B0}=n_i^2 / N_B$，$N_B$ 是 base doping concentration.

解出上面的方程，可以得到：

$$ n'(x)=n_{B0} (e^{q V_{BE}/kT}-1) \dfrac{\sinh \left(\dfrac{W_B-x}{L_B}\right)}{\sinh (W_B/L_B)} $$

由于在制造过程中，基极很窄（base widths ≈ 0.1 μm），可认为 $W_B \ll L_B$，而 $\sinh x$ 在 0 附近约等于 $x$，所以有：

$$ n'(x) = n'(0)\frac{W_B-x}{W_B}\\ = \frac{n_{iB}^2}{N_B} (e^{q V_{BE}/kT}-1) \left( 1 - \frac{x}{W_B}\right) \tag{8.2.6} $$

显然，$n'(x)$ reduces to a straight line，从图像中也可以近似看出这一点。

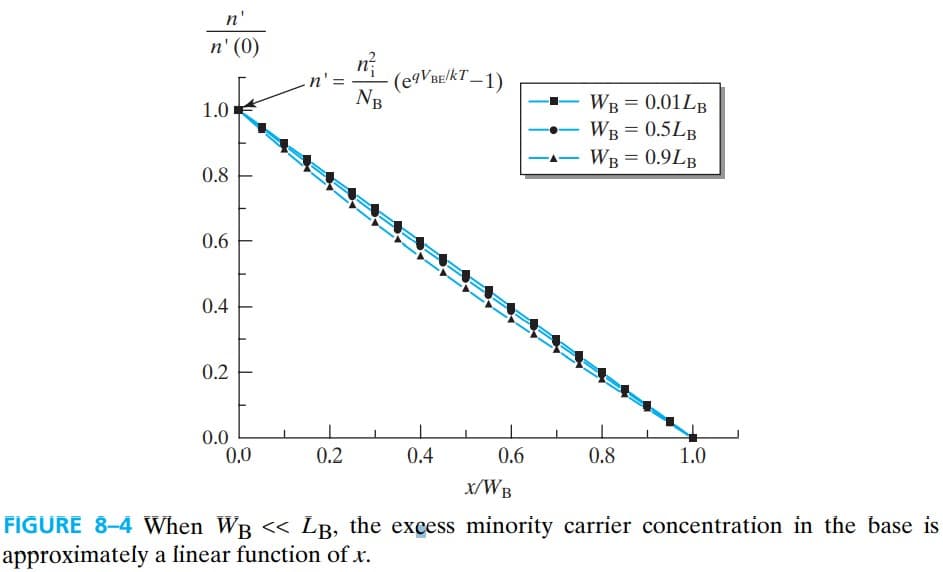
将上述结论代入 $I_C$：

$$ \begin{aligned} I_C &= A_E J_n = \left|A_E q D_B \frac{\dif n}{\dif x}\right|\\ &= A_E q D_B \frac{n'(0)}{W_B} （代入上面的解）\\ &= A_E q \frac{D_B}{W_B} \frac{n_{iB}^2}{N_B} (e^{q V_{BE}/kT}-1) \end{aligned} \tag{8.2.7} $$

$A_E$ 是 BJT 的面积，准确来说是射级的面积（就是少子注入的面积），$n_{iB}$ 是基区材料的 intrinsic carrier concentration

我们定义一个新的变量 base Gummel number：$G_B$

$$ G_B = \frac{n_i^2}{n_{iB}^2} \frac{N_B}{D_B} W_B = \frac{n_i^2}{n_{iB}^2} \frac{p}{D_B} W_B \tag{8.2.10} $$

其中，$N_B$ 是基区掺杂浓度，$p$ 是基区 majority carrier concentration. 上面假设的是基区 uniform 掺杂，如果是 nonuniform 掺杂，则可以用积分：

$$ G_B = \int_0^{W_B} \frac{n_i^2}{n_{iB}^2} \frac{p}{D_B} \dif x \tag{8.2.11} $$

这样一来，$I_C$ 方程可以变为：

$$ \begin{aligned} I_C &= A_E \frac{q n_i^2}{G_B} (e^{q V_{BE}/kT}-1)\\ &= I_S (e^{q V_{BE}/kT}-1) \end{aligned} $$

通过作 Gummel plot 图（fig 8-5 ），可以求出 $G_B$：$A_E q n_i^2$ 除以 x 轴的截距

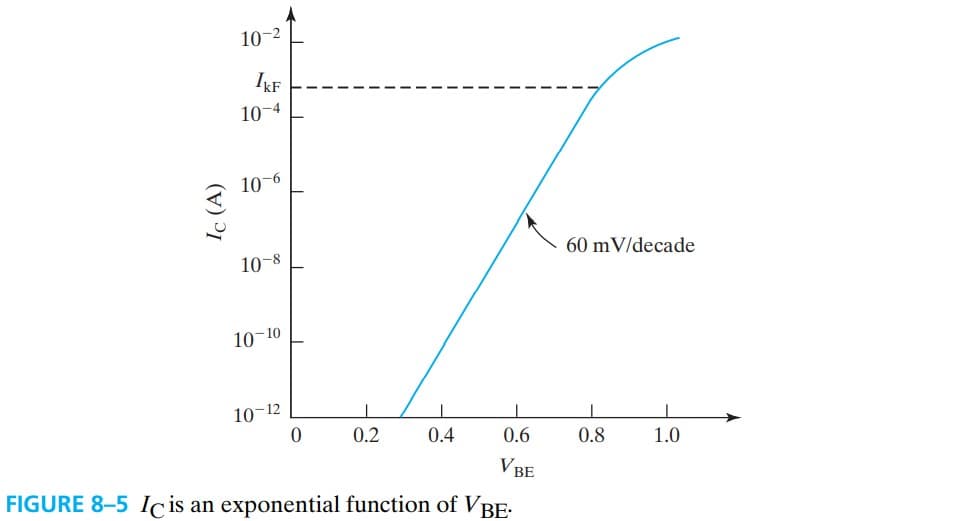
$G_B$ 基本上包含了所有可能影响 $I_C$ 的内部因素：

  • $n_{iB}$ 材料
  • $D_B$
  • $N_B$ 或 $p$ 参杂浓度

8.2.1 High-Level Injection Effect

注意到 Fig 8-5 中，在 $V_{BE}$ 较大时，$I_C$ 斜率下降，变成了曲线，the decrease in the slope of the curve at high $I_C$ called high-level injection effect

在 $V_{BE}$ 较大时，注入的 $n'$ 已经大于掺杂浓度 $N_B$，此时称为 high-level injection，根据电中性条件：

$$ n' = p' \gg N_B $$

也就是说：

$$ n \approx p $$

根据 pn 结中的推论：

$$ n \approx p \approx n_i e ^{qV_{BE}/2kT} $$

从而：

$$ G_B \propto p = n_i e ^{qV_{BE}/2kT} $$

从而：

$$ I_C \propto n_i e ^{qV_{BE}/2kT} \tag{8.2.17} $$

所以在 Fig 8-5 的转折处，inverse slope 已经变成了 120 mV/decade，但由于 $I_C$ 较大使得 IR drop 对 $V_{BE}$ 的影响较大，导致这里不是 straight line 而是 curve。另外，图中的 $I_{kF}$ 是 knee current，这个在 BJT model for simulation 中是一个有用的参数。

8.3 Base Current

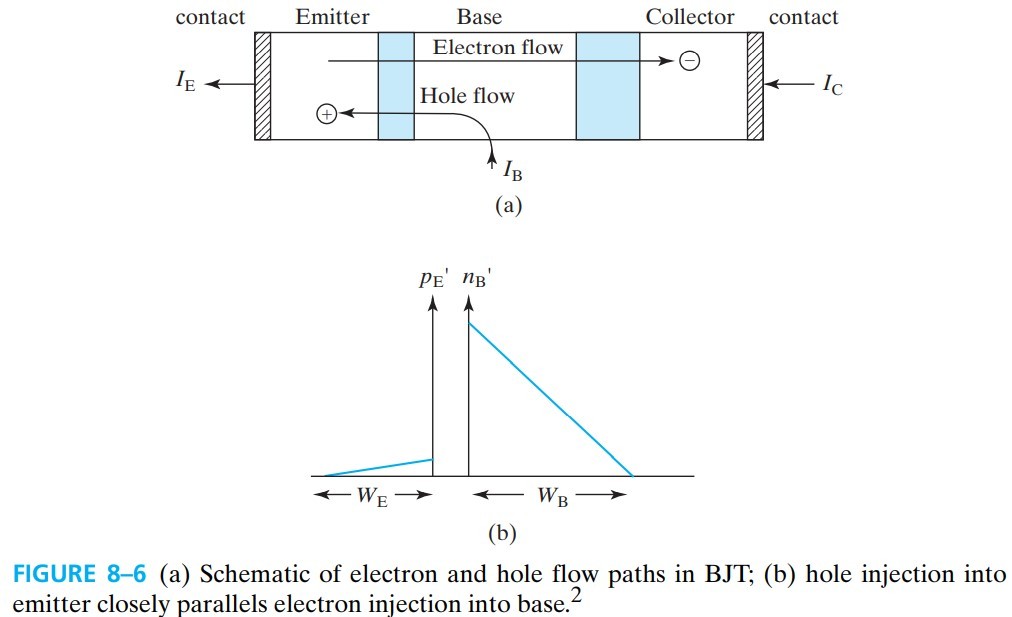
Emitter 发射的电子要到 base，base 发射的空穴要到 emitter，这两个是类似的（但不是完全对称，注意前面都是 $A_E$），所以上面推导的公式可以同样用来求 $I_B$

$$ I_B = A_E \frac{q n_i^2}{G_E} (e^{q V_{BE}/kT}-1) \tag{8.3.1}\\ G_E = \int_0^{W_E} \frac{n_i^2}{n_{iE}^2}\frac{n}{D_E} \dif x\\ n=n(x) $$

$G_E$ 是 emitter Gummel number

对比 $G_E$ 和 $G_B$ 我们容易发现，由于射级是重掺杂，所以 $G_E$ 中的 $n$ 远大于 $G_B$ 中的 $p$，所以 $I_B$ 远小于 $I_C$，因此 BJT 能起到放大的作用。

半导体器件 figure8-6

8.4 Current Gain

为了衡量 BJT 的放大性能，我们定义两个参数：

  • common-emitter current gain: $\beta_F \equiv \dfrac{I_C}{I_B} \tag{8.4.1}$
  • common-base current gain: $\alpha_F = \dfrac{I_C}{I_E}=\dfrac{I_C}{I_B+I_C}$

由于 $I_E=I_B+I_C$，我们可以得出 $\beta_F$ 与 $\alpha_F$ 的关系：

$$ \alpha_F =\dfrac{I_C}{I_B+I_C}=\dfrac{I_C/I_B}{1+I_C/I_B}=\frac{\beta_F}{1+\beta_F} \tag{8.4.3} $$$$ \beta_F = \frac{I_C}{I_E-I_C}=\frac{I_C/I_E}{1-I_C/I_E}=\frac{\alpha_F}{1-\alpha_F} \tag{8.4.4} $$

$\alpha_F$ 大约是 0.99（接近于1），根据上面的关系式，$\beta_F$ 是一个很大的值（100以上）。

我们将上两节推导的 $I_C,I_B$ 代入，可以得到：

$$ \beta_F = \frac{G_E}{G_B}=\frac{D_B W_E N_E n_{iB}^2}{D_E W_B N_B n_{iE}^2} $$

$D$ 和 $W$ 的取值范围有限，影响不大，主要是 $N_B$ 和 $N_E$ 起作用，所以 emitter 要重掺杂 $N_E \gg N_B$

另外，为了衡量射级注入的电子（$I_E$）有多少转变为了 $I_C$，我们定义 emitter efficiency：

$$ \gamma_E = \frac{I_C}{I_E}=\frac{I_E-I_B}{I_E}=\frac{I_C}{I_C+I_B}=\frac{1}{1+G_B/G_E} $$

8.4.1 Emitter Bnad Gap Narrowing

要增大 $\beta_F$，提高 emitter 的掺杂浓度 $N_E$ 是一种方法，但不幸的是，这会产生 heavy doping effect，导致晶体结构（禁带宽）发生改变，使得 $n_{iE}^2$ 变大：

$$ n_{iE}^2 = n_i^2 e^{\Delta E_{gE}/kT} $$

8.4.2 Gummel Plot and βF Fall-Off at High and Low $I_C$

半导体器件 figure8-8

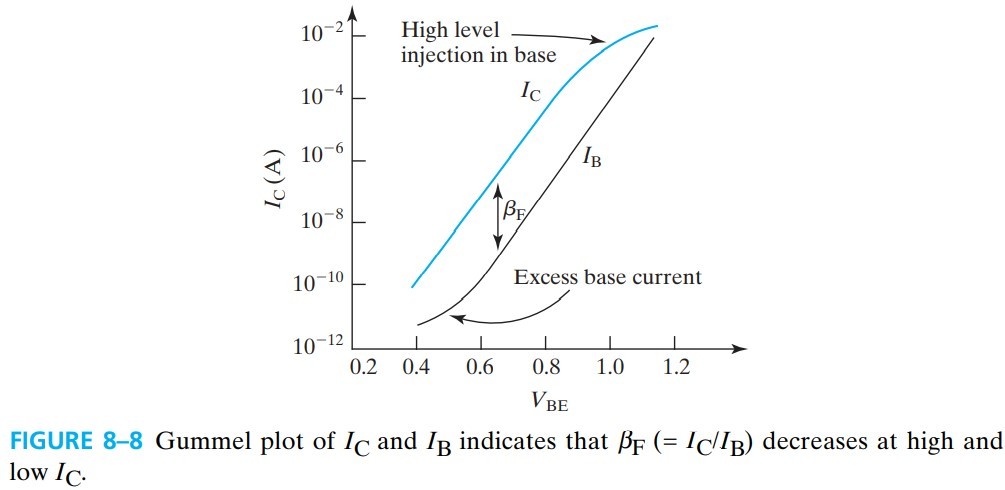
$\beta_F$ 在 $I_C$ 很大或很小时都会下降。

前者的原因在 8.2.1 High-Level Injection Effect 中说过了。因为 $N_E$ 比较大，所以 $I_B$ 不会出现 High-Level Injection Effect.

后者的原因是 4.9.1 the space-charge region (SCR) current

8.5 Base-Width Modulation by Collector Voltage

半导体器件 figure8-10

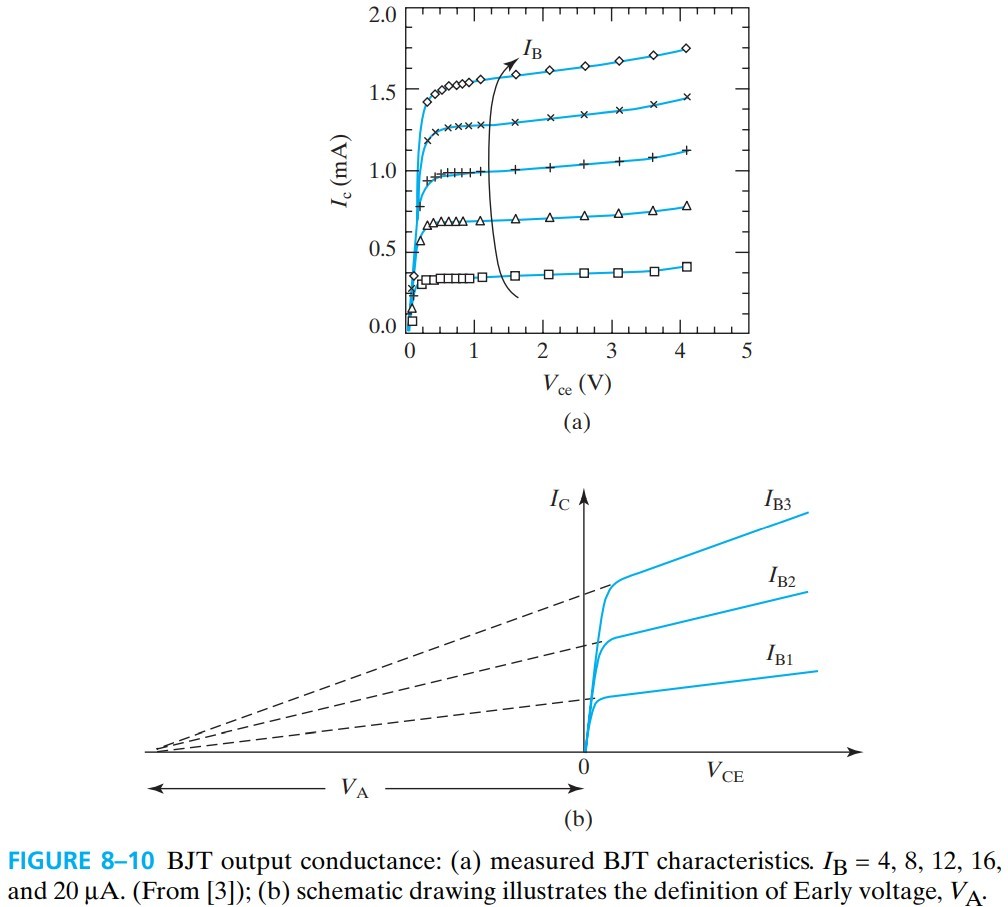
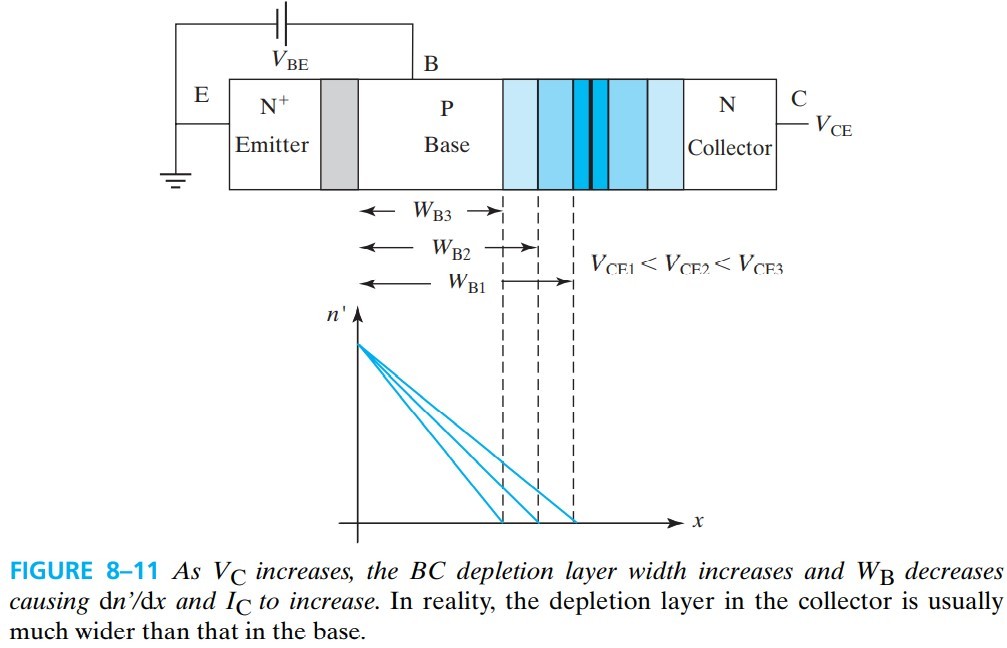
实际 $I_C$-$V_{CE}$ 曲线并不是平的，而是有一定斜率的，用 output conductance $\partial I_C / \partial V_{CE}$，这是由于 base-width modulation （见下图）。

半导体器件 figure8-11

如果反向延长 $I_C$-$V_{CE}$ 曲线，会与横轴交与 Early voltage, $V_A$，从而 output resistance 为：

$$ r_0 \equiv \left( \frac{\partial I_C }{ \partial V_{CE}} \right)^{-1} = \frac{V_A}{I_C} \tag{8.5.1} $$

我们希望曲线能平一点，即 $r_0$ 大一点，即 $V_A$ 大一点。$V_A\approx 50$V，可以通过下面几种方法增大：

  1. increase the base width
  2. increase the base doping concentration, $N_B$, or
  3. decrease the collector doping concentration, $N_C$.

然而前 2 个会导致 $\beta_F$ 下降，所以只能用第三种方法。

8.7 Transit Time and Charge Storage

当 BE 正偏时，会有多余的 holes 和 electrons 存在于 emitter, base 以及之间的 depletion layer，我们定义这部分多余的电荷为 $Q_F$，而 $Q_F$ 与 $I_C$ 满足如下关系：

$$ \tau_F \equiv \frac{Q_F}{I_C} $$

上面这条式子可以理解为：$Q_F$ 存储 $\tau_F$ 时间后才会变为 $I_C$，因此 $\tau_F$ 限制了 BJT 在高频时的速度。

8.7.1 Base Charge Storage and Base Transit Time

我们可以简单运算一下 $Q_{F}$ 在基区那部分的过剩电荷 $Q_{FB}$，看 FIg 8-15，图中三角形部分就是 $Q_{FB}$，即：

$$ Q_{FB} = q A_E \cdot n'(0) \cdot W_B / 2 $$

而 $I_C= A_E q D_B \frac{n'(0)}{W_B}$，代入上式可以得到：

$$ \frac{Q_{FB}}{I_C} \equiv \tau_{FB} = \frac{W_B^2}{2 D_B} $$

$\tau_{FB}$ 就是 base transit time. 可以看出，要提高速度，必须要减小 $\tau_{FB}$，也就是要减小 $W_B$

8.7.3 Drift Transistor-Built-In Base Field

此外，我们可以在 base 建立一个 drift field 来使得电子能更快地通过 base，就是令 base 为不均匀掺杂，如图 Fig 8-16

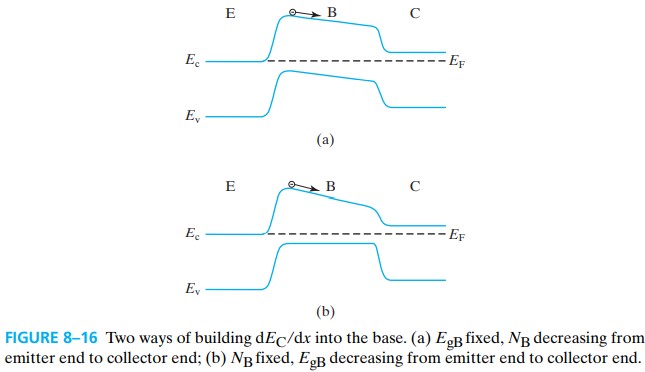
一般在制造过程中，离子注入就会自然形成这个梯度

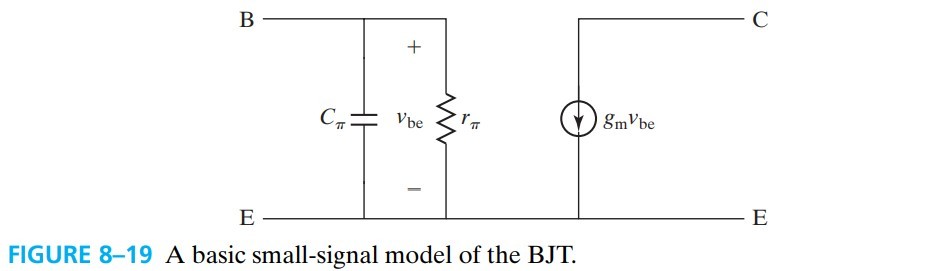
8.8 Small-Signal Model

如果 $V_{BE}$ 不在 0 附近，那么 $I_C=I_S (e^{q V_{BE}/kT}-1)$ 就可以简化为：

$$ I_C = I_S e^{q V_{BE}/kT} $$

如果此时有个小信号 $v_{BE}$ 加在 BE 端，那么就会有相应的电流 $g_m v_{BE}$，即：

$$ g_m \equiv \frac{\dif I_C}{\dif V_{BE}}=\frac{q}{kT} I_S e^{q V_{BE}/ kT}=I_C/\frac{kT}{q} $$

此时，输入端 BE 端对外等效为一个 $C_\pi$ 和 $r_\pi$ 并联，如图 fig 8-19，我们可以计算出它们的值：

$$ \frac{1}{r_\pi} = \frac{\dif I_B}{\dif V_{BE}} = \frac{1}{\beta_F} \frac{\dif I_C}{\dif V_{BE}}=\frac{g_m}{\beta_F}\\ r_\pi = \beta_F / g_m $$$$ C_\pi = \frac{\dif Q_F}{\dif V_{BE}}=\frac{\dif}{\dif V_{BE}} \tau_F I_C=\tau_F g_m $$
半导体器件 figure8-19
Device Fabrication Technology