系列
半导体器件
MOS Transistor

MOS Transistor

$$ \begin{align*} \newcommand{\dif}{\mathop{}\!\mathrm{d}} \newcommand{\belowarrow}[1]{\mathop{#1}\limits_{\uparrow}} \newcommand{\bd}{\boldsymbol} \newcommand{\L}{\mathscr{L}} \end{align*} $$

6.1 Introduction to the MOSFET

半导体器件 figure6-1

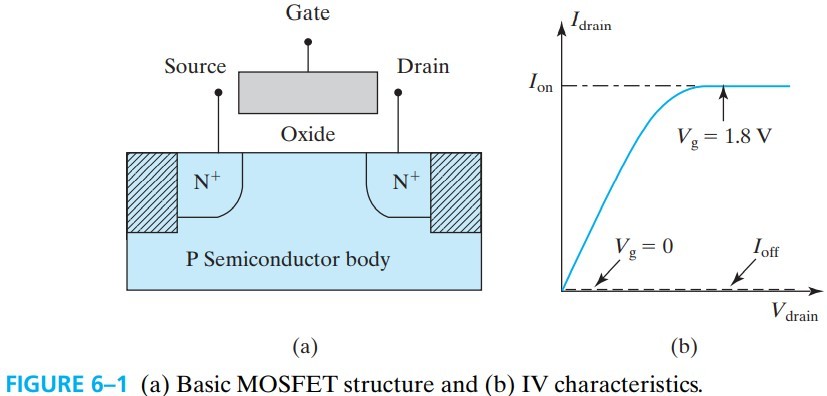
MOSFET 的基本结构如上，左右两个 PN 结叫 source 和 drain，一个用于输入载流子，另一个则用于流出载流子。 FET 代表 field-effect transistor，指的是用过 gate 来开关 transistor，当 $V_g>V_t$ 时，就有电流（如图 fig 6-1b）. 图中斜阴影部分叫 shallow-trench-isolation. ${\rm Si-SiO_2}$ 表面有很高的 threshold voltages $V_t$，从而避免产生 inadvertent surface inversion path

半导体器件 figure6-6
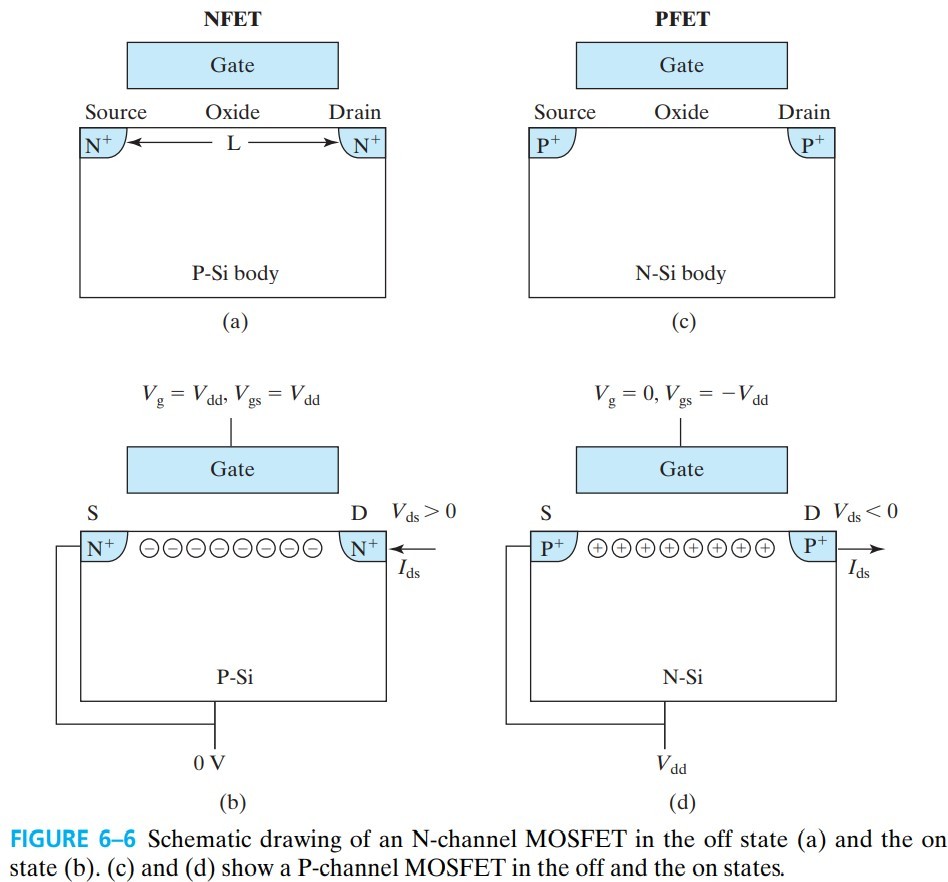
  • N-channel MOSFET
    • The conduction channel (i.e., the inversion layer) is electron rich or N-type（Fig. 6–6b）
    • Body is connected to the lowest voltage, 0V
    • When $V_g=V_{dd}$, on
  • P-channel MOSFET
    • The conduction channel is hole rich or P-type
    • Body is connected to the lowest voltage, $V_{dd}$
    • When $V_g=0$, on

$V_{dd}$ 是 power-supply voltage. 从上可以看出，NFET 和 PFET 的工作方式恰好相反。

实际电路中两种 FET 都有用到，称为 CMOS or complementary MOS circuits

6.3 Surface Mobilities and High-Mobility FETs

我们希望 MOSFET 能导通大电流，并且能快速对电容 $C_\text{oxe}$ 充放电，所以我们需要研究 inversion layer 的载流子 mobility

设加一个小电压 $V_{ds}$，则电流 $I_{ds}$ 为：

$$ \begin{aligned} I_{ds}&=W\cdot Q_\text{inv}\cdot v\\ &= W Q_\text{inv} \mu_{ns} \mathscr{E}\\ &= W Q_\text{inv} \mu_{ns} V_{ds}/L\\ &=W C_\text{oxe} (V_{gs}-V_t)\mu_{ns} V_{ds} / L \end{aligned} \tag{6.3.1} $$

其中，

  • $W$ 是 channel width（横截面）
  • $Q_\text{inv}\;{\rm (C/cm^2)}$ 是 inversion charge density（见公式 $(5.5.3)$）
  • $\mathscr{E}$ 是channel electric field
  • $L$ 是 channel length
  • $\mu_{ns}$ 是 electron surface mobility，也叫 effective mobility
  • 我们规定 $I_{ds}$ 方向在 NFET 中是 D-to-S 为正，在 PFET 中是 S-to-D 为正，故它始终是正的

表面处的 $\mu{ns}$ 和 $\mu\_{ns}$ 比体内小，它与 inversion charge layer 中的平均电场有关。我们设 inversion charge layer 上下表面的电场分别为 top：$\mathscr{E}\_t$ 和 bottom：$\mathscr{E}\_b$，可以用下面公式求出：

$$ \mathscr{E}_b = -Q_\text{dep}/\varepsilon_s \tag{6.3.2} $$

根据 $(5.4.4)$，有：

$$ V_t = V_\text{fb}+\phi_{st}-Q_\text{dep}/C_\text{oxe} $$

所以有：

$$ \mathscr{E}_b = \frac{C_\text{oxe}}{\varepsilon_s}(V_t-V_\text{fb}-\phi_{st}) \tag{6.3.4} $$$$ \begin{aligned} \mathscr{E}_t &= -(Q_\text{dep}+Q_\text{inv})/\varepsilon_s\\ &=\mathscr{b}-Q_\text{inv}/\varepsilon_s\\ &=\mathscr{b}-\frac{C_\text{oxe}}{\varepsilon_s} (V_{gs}-V_t)\\ &= \frac{C_\text{oxe}}{\varepsilon_s} (V_{gs}-V_\text{fb}-\phi_{st}) \end{aligned} $$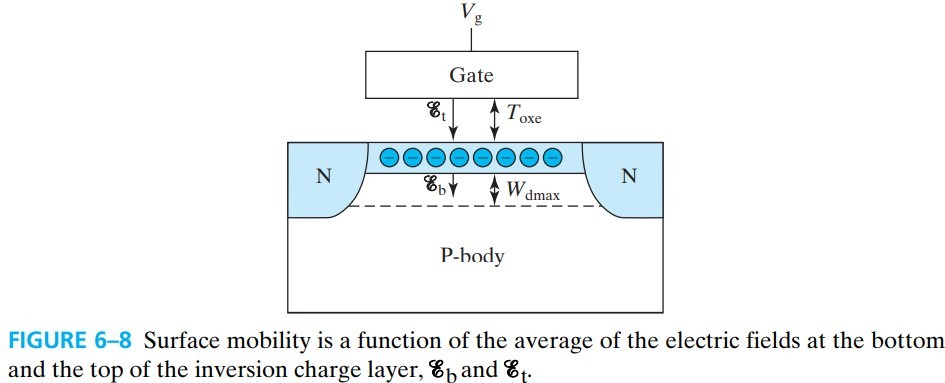
半导体器件 figure6-8

对 inversion layer 使用高斯定理，有：

$$ \begin{aligned} \frac{1}{2}(\mathscr{E}_b+\mathscr{E}_t) &= \frac{C_\text{oxe}}{2 \varepsilon_s}(V_{gs}+V_t-2V_\text{fb}-\phi_{st})\\ &\approx \frac{C_\text{oxe}}{2 \varepsilon_s}(V_{gs}+V_t+0.2 \text{V})\\ &= \frac{\varepsilon_\text{ox}}{2 \varepsilon_s T_\text{oxe}} (V_{gs}+V_t+0.2 \text{V})\\ &= \frac{V_{gs}+V_t+0.2 \text{V}}{6 T_\text{oxe}}\\ & \text{ for }{\rm N^+}\text{ poly-gate NFET} \end{aligned} \tag{6.3.6} $$

$\mu_{ns}$ 与 $(\mathscr{E}\_b+\mathscr{E}\_t)/2$ 或与 $Q\_\text{dep}+Q\_\text{inv}/2$ 有一定函数关系，对实验数据拟合后可以得到 $(6.3.7)$：

$$ \mu_{ns} = \frac{540 {\rm cm^2/Vs}}{1+\left( \dfrac{V_{gs}+V_t+0.2\text{V}}{5.4 T_\text{oxe}} \right)^{1.85}} \tag{6.3.7} $$

类似的，$\mu_{ns}$ 与 $(\mathscr{E}_b+1.5 \mathscr{E}_t)/2$ 也有一定关系：

$$ \mu_{ps} = \frac{185 {\rm cm^2/Vs}}{1-\left( \dfrac{V_{gs}+1.5V_t-0.25 \text{V}}{5.4 T_\text{oxe}} \right)} \tag{6.3.8} $$

这俩公式看起来怪恐怖的。在 NFET 中 $V_{gs}$ 和 $V_t$ 为正，在 PFET 中 $V_{gs}$ 和 $V_t$ 为负。当 $(\mathscr{E}_b, \mathscr{E}_t)$ 增强时，$\mu_{ns}$ 和 $\mu_{ps}$ 会减小，因为电场越大，载流子就越靠近表面，就容易受 surface roughness scattering 影响。

晶面指数对 $\mu_s$ 也会有影响，所以我们选择 $[100]$ 面，此时的 $\mu_{ns}$ 最大，但 $\mu_{ps}$ 不是最大。

6.4 MOSFET Vt, Body Effect, And Steep Retrograde doping

半导体器件 figure6-13

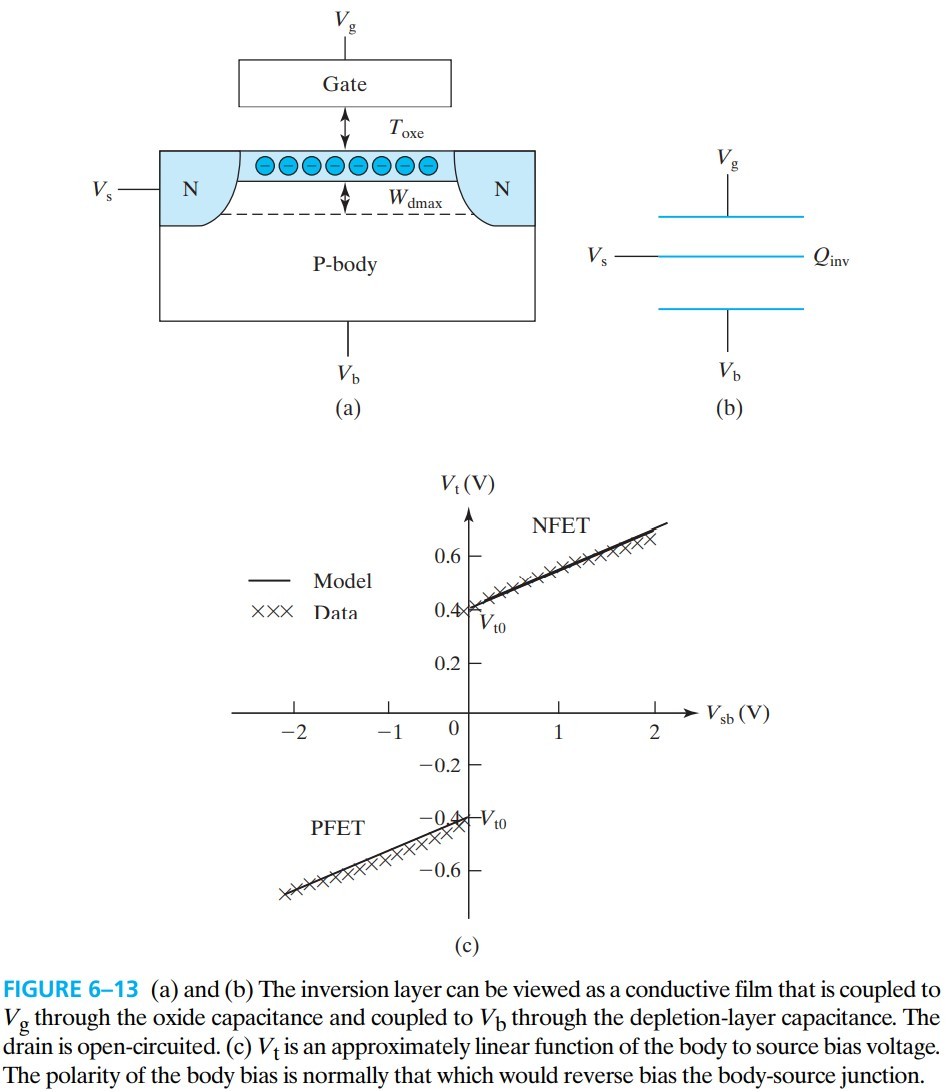
我们将 inversion layer 看作一个连接 source 和 drain 的 N-type film，上面的电压为 $V_s$. 该薄层与 gate 形成了一个电容，同时与下面的 depletion layer 也形成了电容。这两个电容我们在 $(5.6.2)$ 和 $(5.5.3)$ 中求过，这里再写一次：

$$ C_\text{dep} = \frac{\varepsilon_s}{W_\text{dmax}} \tag{6.4.1} $$$$ Q_\text{inv} = -C_\text{oxe} (V_{gs}-V_t) \tag{6.4.2}\\ 负号是因为电压与电荷不在同一极板 $$

如果我们在 source 和 body 之间加一电压 $V_{sb}$，这样相当于在 $C_\text{dep}$ 加电压，所以 $(6.4.2)$ 变为：

$$ \begin{aligned} Q_\text{inv} &= -C_\text{oxe}(V_{gs}-V_t)+C_\text{dep}V_{sb}\\ &= - C_\text{oxe}\left( V_{gs} - \left( V_t + \frac{C_\text{dep}}{C_\text{oxe}} V_{sb}\right) \right) \end{aligned} \tag{6.4.4} $$

我们可以将 $V_t$ 看作是 $V_t(V_{sb})$，从而（用 $V_{t0}$ 代替原来的 $V_t$）：

$$ Q_\text{inv} = -C_\text{oxe} (V_{gs} - V_t(V_{sb})) \tag{6.4.5} $$$$ V_t(V_{sb}) = V_{t0}+\frac{C_\text{dep}}{C_\text{oxe}} V_{sb}=V_{t0}+\alpha V_{sb} \tag{6.4.6}\\ \alpha = C_\text{dep}/C_\text{oxe} = 3 T_\text{oxe}/W_\text{dmax} $$

式子中的 3 来自于硅和二氧化硅的介电常数比值。

我们将 $V_t$ 受 body bias 调控的现象称为 body effect，$\alpha$ 称为 body-effect coefficient. 一般来说，我们不会让 source 和 body 形成 forward bias，否则会产生电流。当然，我们也不希望 reverse bias，因为这样会增大 $V_t$，减小 $I_{ds}$，减慢速度。要减小 body effect，可以 minimizing the $T_\text{ox}/W_\text{dmax}$ ratio，即使用 thin oxide

现代 transistor 都采用 steep retrograde body doping profiles（表面浓度远大于内部），这样 $\alpha$ 不随 $V_{sb}$ 变化。以前的 MOSFETS 的浓度都是线性变化的，导致 $V_t$ 与 $V_{sb}$ 并不是线性关系，我们可以将 $(5.4.3)$ 中的 $2\phi$ 项替换成 $2\phi+V_{sb}$：

$$ \begin{aligned} V_t &= V_{t0}+\frac{\sqrt{q N_a 2 \varepsilon_s}}{C_\text{oxe}}(\sqrt{2 \phi_B+V_{sb}} - \sqrt{2 \phi_B})\\ &\equiv V_{t0} + \gamma(\sqrt{2 \phi_B+V_{sb}} - \sqrt{2 \phi_B}) \end{aligned} \tag{6.4.8} $$

$γ$ is called the body-effect parameter

6.5 Qinv in MOSFET

考虑在 drain 上加一电压 $V_d$（如图 fig 6-15），这样沟道上的电压 $V_c$ 随 $x$ 变化，我们写成 $V_c(x)$

半导体器件 figure6-15

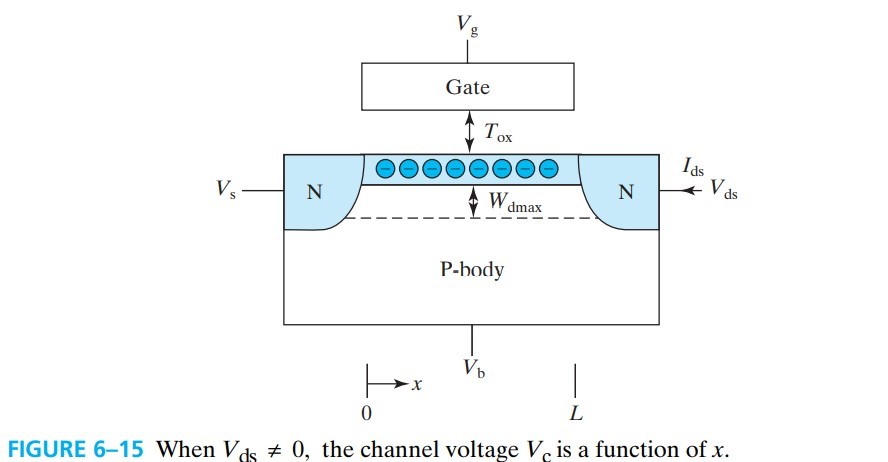
原本 $C_\text{oxe}$ 上的电压是 $V_g$，现在则变成了 $V_g-V_c(x)$，这么一来 inversion layer 上的电荷就会减少：

$$ Q_\text{inv}(x) = -C_\text{oxe} (V_{gs} - V_t(V_{sb})) \tag{6.4.5}\\ \Downarrow $$$$ \begin{aligned} Q_\text{inv}(x) &= -C_\text{oxe} (V_{gs}-V_{cs} - V_t(V_{sb}+V_{cs}))\\ &= -C_\text{oxe} (V_{gs}-V_{cs} - V_{t0} - \alpha(V_{sb}+V_{cs}))\\ &=-C_\text{oxe} (V_{gs}-V_{cs} - (V_{t0} + \alpha V_{sb}) -\alpha V_{cs})\\ &= -C_\text{oxe} (V_{gs}-(1+\alpha)V_{cs} - (V_{t0} + \alpha V_{sb}))\\ &=-C_\text{oxe} (V_{gs}-mV_{cs} - (V_{t0} + \alpha V_{sb})) \end{aligned} \\\tag{6.5.1} m \equiv 1+\alpha = 1+C_\text{dep}/C_\text{oxe}=1+3 T_\text{oxe}/W_\text{dmax} $$

$m$ 一般在 $1.2$，但为了方便计算可以取 $1$.

（下面这段话我觉得放在 6.4 会比较合适）有时候我们也把 body 叫 back gate，因为它也能调控 channel charge. 这种调控 $Q_\text{inv}$ 的能力叫 bulk-charge effect，$m$ 叫 bulk-charge factor

6.6 Basic MOSFET I-V Model

还记得 $(6.3.1)$ 的公式吗？我们把 $Q_\text{inv}(x)$ 代入：

$$ \begin{aligned} I_{ds} &= W\cdot Q_\text{inv}(x) \cdot v\\ &=W\cdot Q_\text{inv}(x) \cdot \mu_{ns} \mathscr{E}\\ &=W \cdot C_\text{oxe} (V_{gs} - V_t-mV_{ds}) \cdot \mu_{ns} \frac{\dif V_{ds}}{\dif x} \end{aligned} \tag{6.6.1} $$

将 $\dif x$ 移到左边，然后对 $I_{ds}$ 积分，得到：

$$ I_{ds} = \frac{W}{L} C_\text{oxe}\mu_{ns} \left(V_{gs} - V_t-\frac{m}{2}V_{ds}\right)V_{ds} \tag{6.6.4} $$

当 $V_{ds}$ 很小时，我们可以忽略 $\frac{m}{2}V_{ds}$ 项，此时 transistor 就像一个 resistor. 我们可以求出电阻：

$$ \frac{\dif I_{ds}}{\dif V_{ds}} =\frac{W}{L} C_\text{oxe}\mu_{ns} \left( V_{gs} - V_t-mV_{ds} \right) $$

令电阻为 $0$，可以求出：

$$ V_{ds} = V_\text{dsat} = \frac{V_{gs}-V_t}{m} \tag{6.6.5} $$

$V_\text{dsat}$ 称为 drain saturation voltage，当到达这个电压后，再增大 $V_{ds}$，电流也不会变大（毕竟电阻怎么也不会变成负的吧……），最大电流为：

$$ I_\text{dsat} = \frac{W}{2 m L}C_\text{oxe} \mu_{ns} (V_{gs}-V_t)^2 \tag{6.6.6} $$

如果我们将 $V_{ds}$ 代回 $(6.5.1)$，会发现此时 $Q_\text{inv}=0$，即 inversion layer 不见了。我们称为 channel pinch-off. 如果持续增大 $V_{ds}$，会出现一个 pinch-off region，across which the voltage $V_{ds} − V_\text{dsat}$ is dropped。（如图 fig 6-17e,h）the pinch-off region does not present a barrier to current flow，所以电流不变。

半导体器件 figure6-17

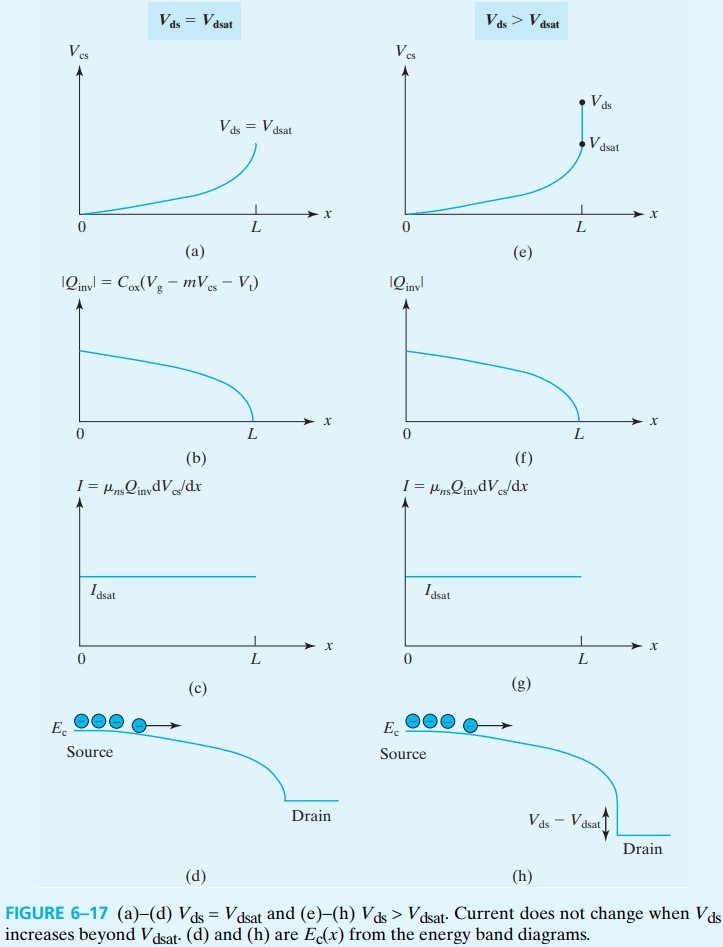
我们可以将 I-V 曲线划分成三个区：

  • $V_{ds} \ll V_\text{dsat}$ 称为 linear region
  • $V_{ds} \gt V_\text{dsat}$ 称为 saturation region，也称为 Ohmic region 或 active region.
半导体器件 figure6-16

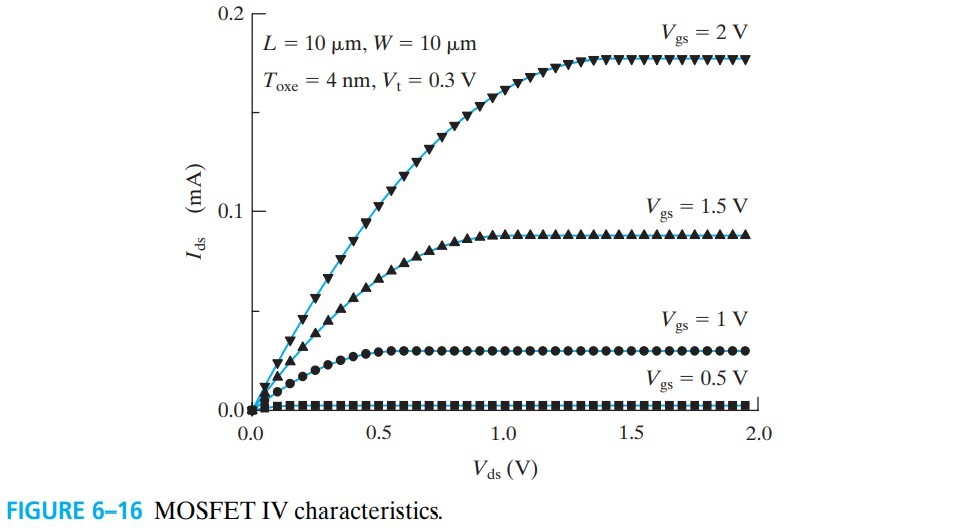
我们用 Transconductance 来衡量 $V_{gs}$ 对电流的控制能力（电流对 $V_{gs}$ 的敏感程度）：

$$ g_m \equiv \left. \frac{\dif I_{ds}}{\dif V_{gs}} \right|_{V_{ds}} $$

由 $(6.6.4)$ 可以求出：

$$ \begin{aligned} g_m &= \frac{W}{L} C_\text{oxe}\mu_{ns} V_{ds}\\ & \leq \frac{W}{L} C_\text{oxe}\mu_{ns} V_\text{dsat}\\ &= \frac{W}{mL} C_\text{oxe}\mu_{ns} (V_{gs}-V_t)\\ &= g_\text{msat} \end{aligned} \tag{6.6.9} $$

6.7 CMOS Inverter - A Circuit Example

下面我们来分析一个简单的CMOS电路实例——反相器。

半导体器件 figure6-7

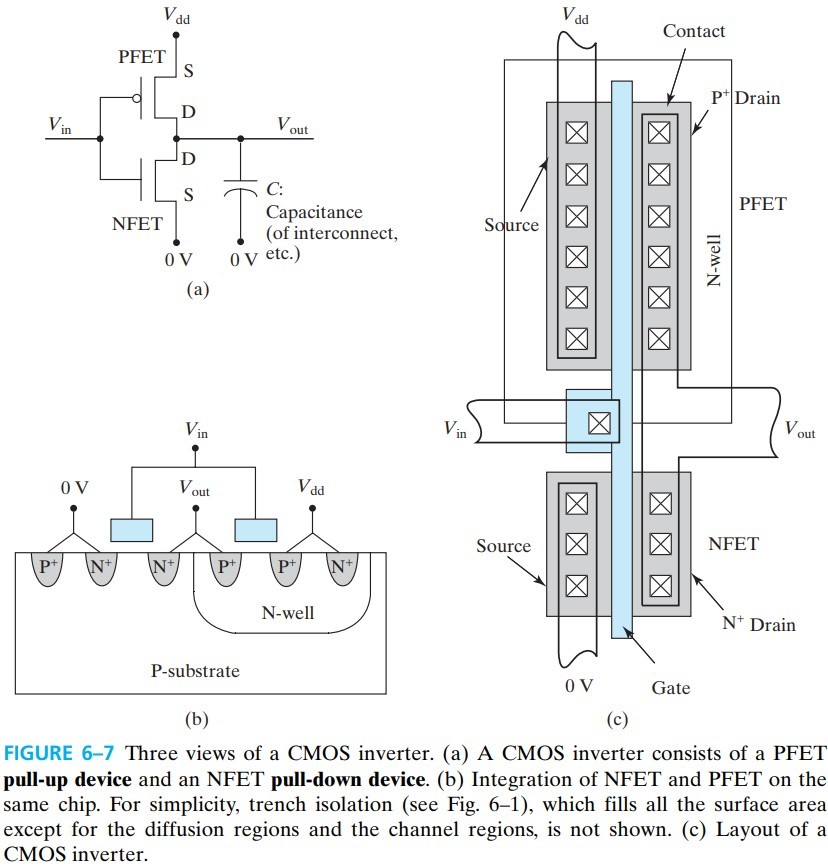
当 $V_\text{in}=V_{dd}$ 时，NFET 开 PFET 关；当 $V_\text{in}=0$ 时，NFET 关 PFET 开。从而实现反相。

6.7.1 Voltage Transfer Curve (VTC)

下面我们来进一步分析 I-V 关系。fig 6-18b 画出了 NET 和 PFET 独立的 IV 曲线。由于 PFET 的 source 是 $2\text{V}$，所以它的 $V_{gs} = V_\text{in} - 2\text{V}$

为了方便分析，我们不妨用 $V_\text{out}$ 作为横轴，其中 NFET $V_{dsN} =V_\text{out}$；PFET $V_{dsP} = V_\text{out} -2 \text{V}$，于是就得到 fig 6-18c。又由于两者是共 $V_\text{in}$ 的，所以图中，同一 $V_\text{in}$ 的实线与虚线的交点就是实际中的 $V_\text{in} / V_\text{out}$ 关系，称为 the voltage transfer characteristic or voltage transfer curve or VTC of the inverter

半导体器件 figure6-18

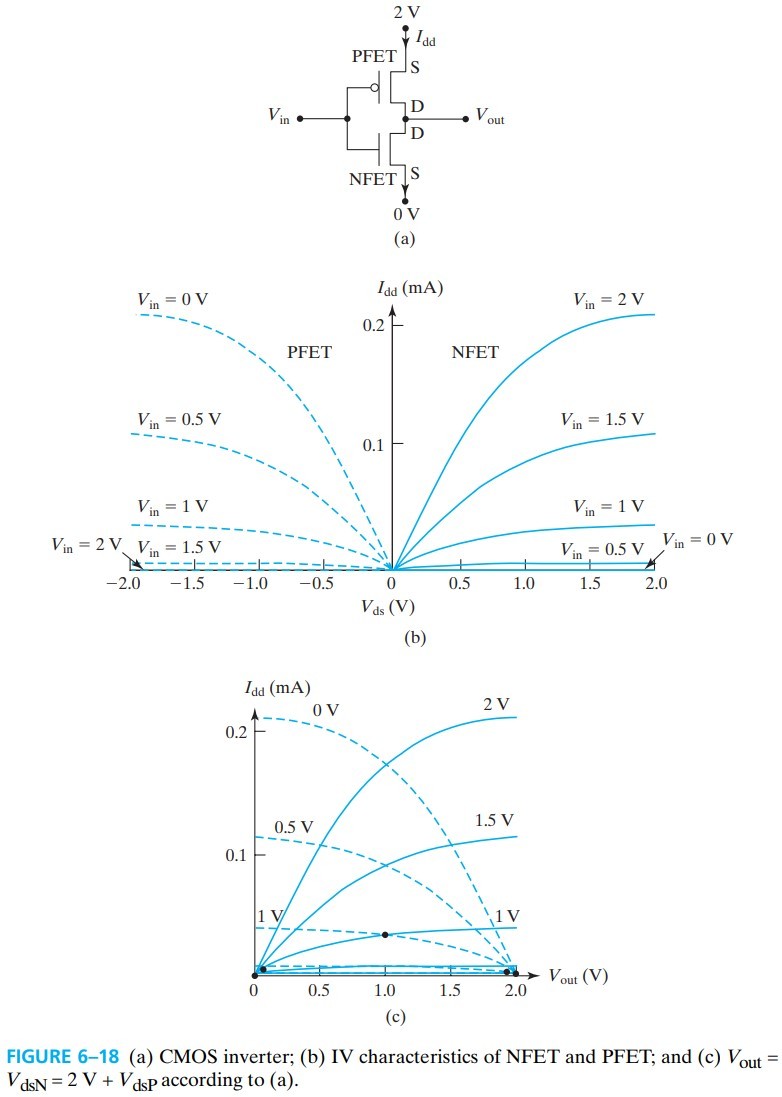
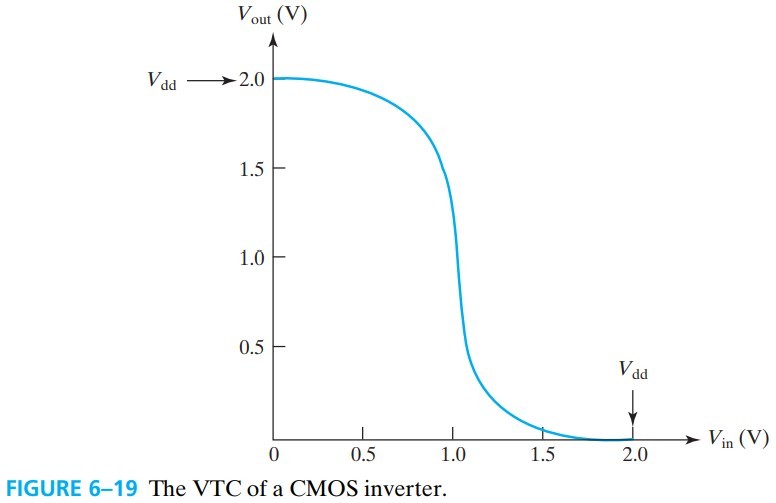
我们希望 VTC 中间越陡越好，这样可以 maximize the noise tolerance. 同时我们还希望 a large gm, low leakage in the off state, and a small in the saturation region. 这些我们会在后面讨论。

半导体器件 figure6-19

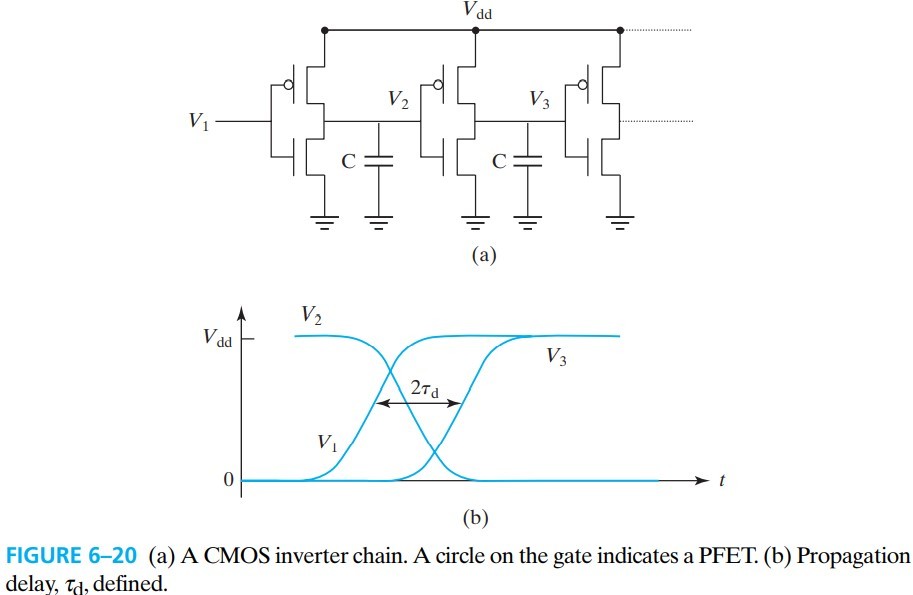
6.7.2 Inverter Speed—The Importance of I_on

Propagation delay 指的是一个输入经过多个串联的 CMOS 后输出的延时，我们一般用 pull-down and pull-up 的平均延迟 $\tau_s$ 来表示。在下图中就是 $V_1$ 上升后，经过 $V_2$ 下拉，再到 $V_3$ 上拉的时间。即电容充放电的时间：

$$ \begin{aligned} \tau_d &= \frac{1}{2}(\text{pull-down delay + pull-up})\\ &\approx \frac{C V_{dd}}{4}\left( \frac{1}{I_{onN}}+\frac{1}{I_{onP}} \right) \end{aligned} \tag{6.7.1}\\ I_{on} \equiv \left. I_\text{dsat}\right|_{\max |V_{gs}|} $$

$C$ 不只是外接电容，还包括器件内部的电容。

半导体器件 figure6-20

6.7.3 Power Consumption

由于器件在电路中并不是时刻都在工作，而是在特定的时钟周期中工作，可以用 activity factor $k$ 来衡量活跃程度。我们用 dynamic power 来衡量工作功耗，则：

$$ P_\text{dynamic} = k CV_{dd}^2 f \tag{6.7.6} $$

另外，当器件关闭时有漏电流，导致 static power, or leakage power or stand-by power

$$ P_\text{static} = V_{dd} I_\text{off} $$

我们会在下一章介绍如何减小漏电流。

$$ P=P_\text{static}+P_\text{dynamic} $$

6.8 Velocity Saturation

在 2.2.2 介绍散射机构时，提到过 saturation velocity，指的是当电场大到一定程度时，受光子散射影响，载流子速度不再提升。即：

$$ v = \frac{\mu_{ns} \mathscr{E}}{1+\mathscr{E}/\mathscr{E}_\text{sat}} \tag{6.8.1} $$

那有没有方法继续提高速度呢？有。方法是使得沟道长度 $L$ 很小，使得载流子来不及发射光子，从而达到比 $\mu_{ns} \mathscr{E}_\text{sat}$ 更快的速度，这种现象称为 velocity overshoot.

6.9 MOSFET I-V Model with Velocity Saturation

考虑了 velocity saturation 后的 I-V 特性如下（把 $(6.8.1)$ 代入到 $(6.6.1)$得到）：

$$ I_{ds} = \frac{\text{long-channel } I_{ds}}{1+\dfrac{V_{ds}}{\mathscr{E}_\text{sat} L}}\\ \text{long-channel }I_{ds} =\frac{W}{L} C_\text{oxe}\mu_{ns} \left(V_{gs} - V_t-\frac{m}{2}V_{ds}\right)V_{ds} \tag{6.6.4} $$

可以看出 $L$ 很大时，Velocity Saturation 的影响变小，就得到我们原来的 I-V 关系，称为 long-channel IV model。

从而新的 $V_\text{dsat}$ 可以用下面的公式求出（经过了简化）：

$$ \frac{1}{V_\text{dsat}}=\frac{m}{V_{gs}-V_t}+\frac{1}{\mathscr{E}_\text{sat}L} \tag{6.9.10}\\ 其中，m =1+3 T_\text{oxe}/W_\text{dmax}\\ \mathscr{E}_\text{sat} = 2v_\text{sat}/\mu_{ns} $$

$v_\text{sat}$ is 8×106 cm/s for electrons and 6×106 cm/s for holes.

从而 $I_\text{dsat}$ 为：

$$ \begin{aligned} I_\text{dsat} &= \frac{W}{2 m L}C_\text{oxe} \mu_{ns} \frac{(V_{gs}-V_t)^2}{1+\dfrac{V_{gs}-V_t}{m \mathscr{E}_\text{sat}L}}\\ &= \frac{\text{long channel } I_\text{dsat}}{1+\dfrac{V_{gs}-V_t}{m \mathscr{E}_\text{sat}L}} \end{aligned} \tag{6.9.11} $$

在两种特殊情况下，上式可以简化：

  1. Long-channel or low $V_{gs}$ case, $\mathscr{E}\_\text{sat}L \gg V\_{gs} − V\_t$

    简化成原本的形式，即：

    $$ \begin{aligned} V_\text{dsat} &= \frac{V_{gs}-V_t}{m}\\ I_\text{dsat} &= \frac{W}{2 m L}C_\text{oxe} \mu_{ns} (V_{gs}-V_t)^2 \end{aligned} \tag{6.9.12} $$

  2. Very short-channel case, $\mathscr{E}\_\text{sat}L \ll V\_{gs} − V\_t$

    $$ \begin{aligned} V_\text{dsat} &\approx \mathscr{E}_\text{sat}L < \frac{V_{gs}-V_t}{m}\\ I_\text{dsat} &= W v_\text{sat} C_\text{oxe} (V_{gs}-V_t-m \mathscr{E}_\text{sat}L) \end{aligned}\tag{6.9.13} $$

要提高 $I_\text{dsat}$，就要提高 $C_\text{oxe}(V_{gs}-V_t)$，即减小 $T_\text{oxe}$ 并减小 $V_t$ 并增大 $V_{gs}$。可惜的是，$T_\text{oxe}$ 受 oxide tunneling leakage and reliability 限制；$V_t$ 受 MOSFET leakage 限制；$V_{gs}$ 则受电源和功耗限制。

6.13 Output Conductance

半导体器件 figure6-23

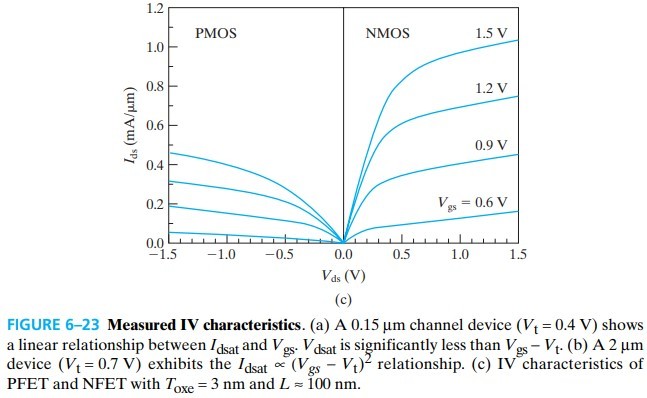
从上图中，注意到 $I_\text{dsat}$ 会缓慢增长，这是由短沟道造成的，斜率称为 output conductance：

$$ g_{ds} = \frac{\dif I_\text{dast}}{\dif V_{ds}} $$

我们希望 $g_{ds}$ 足够小，这样当我们把 MOSFET 当 amplifier 用时，才能得到大的 intrinsic voltage gain（具体模型看书本 230 页）

MOS CapacitorMotion and Recombination of Electrons and Holes