Motion and Recombination of Electrons and Holes
$$ \begin{align*} \newcommand{\dif}{\mathop{}\!\mathrm{d}}\\ \newcommand{\p}{\partial}\\ \newcommand{\bd}{\boldsymbol}\\ \end{align*} $$上一章中,讨论的是电子/空穴在能级之间的移动,而本章讨论的是在空间中的移动。
2.1 Thermal Motion
无外加电场的情况下,carriers 仅做热运动,单个电子的 kinetic energy 为 $E-E_c$,平均 kinetic energy 为:
$$ \frac{\int f(E)D(E)(E-E_c) \dif E}{\int f(E)D(E)\dif E} = \frac{3}{2} kT $$上式对空穴同样适用。由于 $E_k = \frac{1}{2}mv^2$,所以我们可以得到 thermal velocity $v_\text{th}$:
$$ v_\text{th} = \sqrt{\frac{3kT}{m}}\\ m 取 m_n 或 m_p $$电子和空穴的热运动是杂乱无章的, Their directions of motion change frequently due to collisions or scattering with imperfections in the crystal(mean free time≈0.1ps),所以它们的“net thermal velocity”为 0。
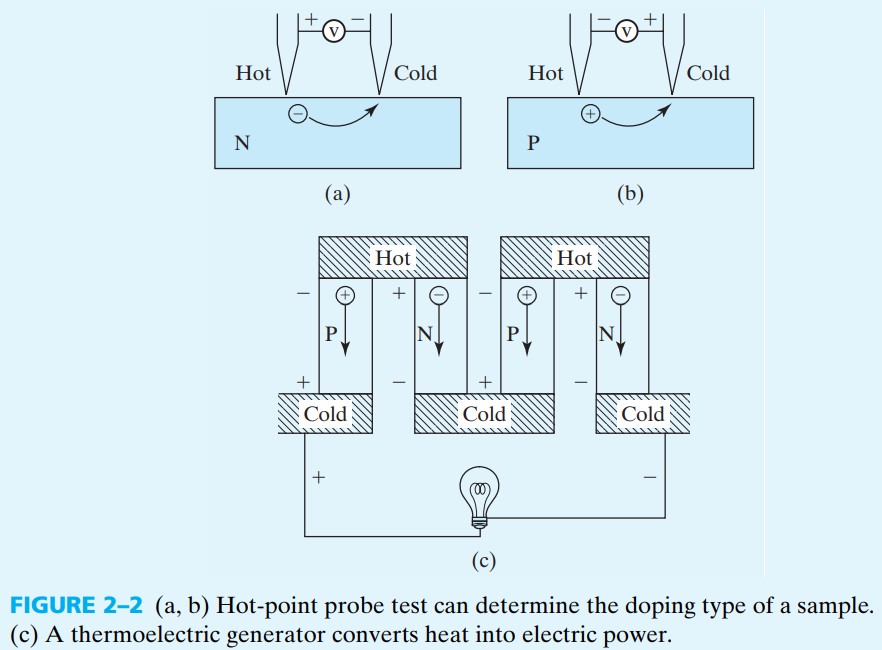
扩展资料:hot-point probe test 法测量半导体类型 和 thermoelectric generator 热发电(用在卫星上),看图 fig 2-2 就能理解。
2.2 Drift
Drift (漂移运动)指载流子在电场下的运动
2.2.1 Electron and Hole Mobilities
在电场下,载流子的净速度不再为0,而是有一个 drift velocity,一般都希望这个速度越大越好,这样器件才快。
假设 mean free time between collisions 为 $\tau_\text{mp}$,并且碰撞会消耗全部动能,那么:
$$ m_p v = q\mathscr{E} \tau_\text{mp} $$为了简化这个式子,我们定义迁移率 mobility $\mu$(单位:$\text{cm}^2/(\text{V}\cdot \text{s})$),表示在某个电场下载流子获得速度的能力:
$$ \begin{cases} v_p =\mu_p \mathscr{E}\\ \mu_p = \dfrac{q \tau_\text{mp}}{m_p} \end{cases} \tag{2.2.3a} $$$$ \begin{cases} v_n = - \mu_n \mathscr{E}\\ \mu_n = \dfrac{q \tau_\text{mn}}{m_n} \end{cases} \tag{2.2.3b} $$因为电子与空穴的速度方向不同,所以多个负号。
| Si | Ge | GaAs | InAs | |
|---|---|---|---|---|
| $\mu_n$ | 1400 | 3900 | 8500 | 30,000 |
| $\mu_p$ | 470 | 1900 | 400 | 500 |
2.2.2 Mechanisms of Carrier Scattering
产生碰撞的原因有两个:
phonon scattering 声子散射
Phonons are the particle representation of the vibration of the atoms in the crystal
ionized impurity scattering 电离杂质散射
这两个分别对总的 $\tau$ 的贡献分别为 $\tau_\text{phonon}$ 和 $\tau_\text{impurity}$,并满足如下关系:
$$ \frac{1}{\tau} = \frac{1}{\tau_\text{phonon}} + \frac{1}{\tau_\text{impurity}}\\ \frac{1}{\mu} = \frac{1}{\mu_\text{phonon}} + \frac{1}{\mu_\text{impurity}} $$$\tau_\text{phonon}$ 和 $\tau_\text{impurity}$ 与温度的关系如下:
$$ \mu_\text{phonon} \propto \tau_\text{phonon} \propto T^{-3/2}\\ \mu_\text{impurity} \propto \tau_\text{impurity} \propto \frac{T^{3/2}}{N_a+N_d} $$图 fig 2-5 对比了电子与空穴的迁移率,可以发现电子的迁移率比空穴大(大约是三倍),这是由于电子的 $m_n$ 比较小。
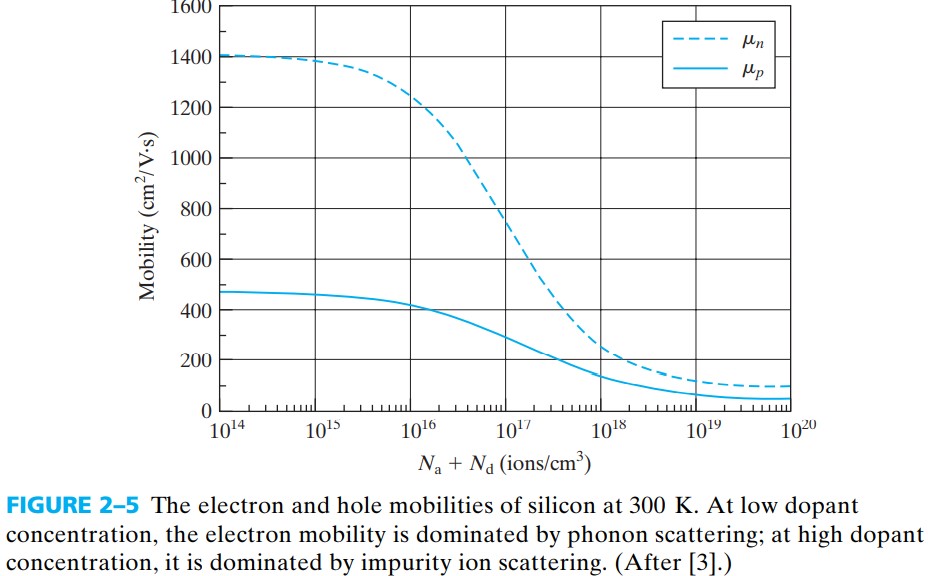
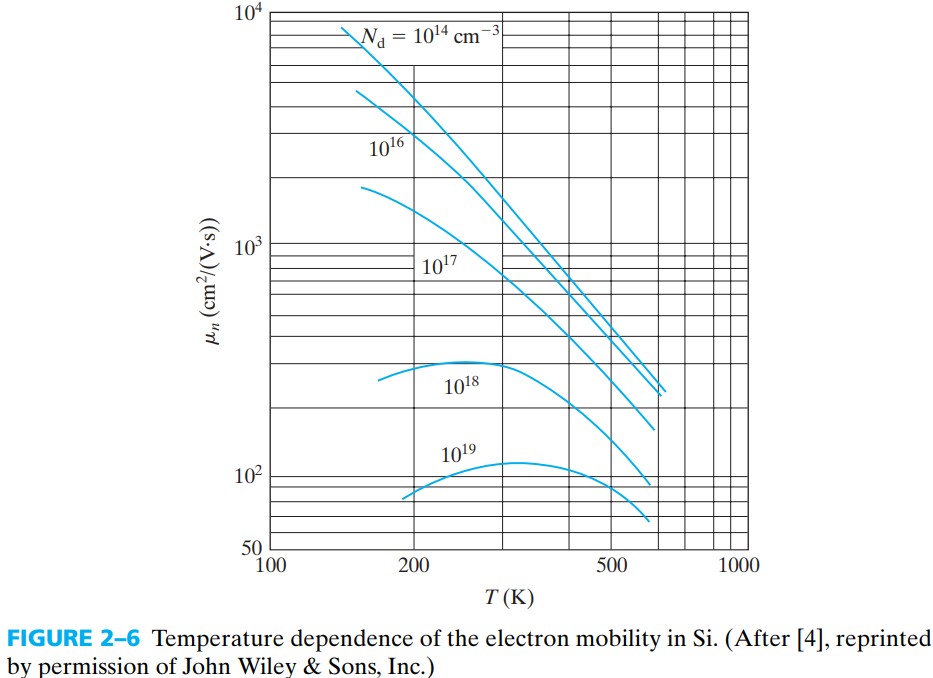
图 fig 2-6 则说明了电子迁移率随温度和掺杂浓度的变化情况。可以看出,在低掺杂下,主要是 phonon scattering 在起作用(因为此时随温度升高,迁移率下降);在高掺杂下,低温时是 impurity scattering 为主导,高温时是 phonon scattering 为主导。
另外,如果想要电阻率随温度变化不大,那么应该选择图中斜率平坦的那条掺杂浓度(即10^19)
扩展:漂移速度增加到 $10^7$ cm/s 后就不会随电场增大而增大,这是因为有新的散射叫 optical phonon scattering,当 $E_k$ 大于 optical phonon energy $E_\text{opt}$ 时,多出来的能量就会变为光子发射出去,所以会存在一个 saturation velocity $v_\text{sat}$。这个限制了器件的速度,因此要提高才行。
2.2.3 Drift Current and Conductivity
知道载流子运动速度后就能求出电流:
$$ J_{p,\text{drift}} = qpv = qp \mu_p \mathscr{E} \tag{2.2.11} $$$$ J_{n,\text{drift}} = qnv = qn \mu_n \mathscr{E} \tag{2.2.12} $$总电流为:
$$ J_\text{drift} = J_{p,\text{drift}} + J_{n,\text{drift}}= (qp \mu_p + qn \mu_n )\mathscr{E} $$我们将括号内的部分定义为导电率 conductivity $\sigma = qp \mu_p + qn \mu_n$,单位 A/V⋅cm
2.3 Diffusion Current
Diffusion is the result of particles undergoing thermal motion,一般来说热运动总是有使各处浓度一致的倾向,当浓度不一致时,热运动就会导致高浓度向低浓度扩散。因此,扩散电流与浓度梯度有关:
$$ J_{n,\text{diffusion}} = q D_n \frac{\dif n}{\dif x} \tag{2.3.2}\\ $$$$ J_{p,\text{diffusion}} =- q D_p \frac{\dif p}{\dif x} \tag{2.3.3} $$$D_n,D_p$ 称为 diffusion constant. 比较令人困惑的就是上两式中,空穴反而需要加负号?!这是因为梯度本身有一个负号,所以空穴反而要加负号才是正电荷电流。
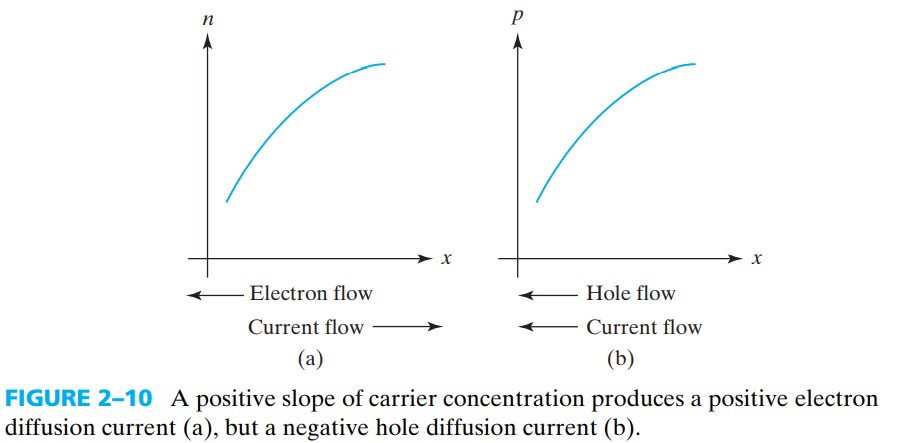
我们暂时不讨论 $D$ 怎么求,在 2.5 中会学到 $D$ 实际上与 $\mu$ 有关。
总电流等于:
$$ J_n = J_{n,\text{drift}} + J_{n,\text{diffusion}} = qn \mu_n \mathscr{E} + q D_n \frac{\dif n}{\dif x}\\ J_p = J_{p,\text{drift}} + J_{p,\text{diffusion}} = qp \mu_p \mathscr{E} - q D_p \frac{\dif p}{\dif x}\\ J=J_n+J_p $$最后提一个小问题:为什么电子和空穴的 drift 电流符号是相同的,而 diffusion 电流符号是相反的?
2.4 Relation between the Energy Diagram and V,E
外加电压会使得能带“弯曲”,正电压会使得正电荷的电势上升(能带下降),负电荷的电势下降(能带下降)。因此,正电压处,$E_c,E_v$ 能带下降(见下图)
The electrons roll downhill like stones in the energy band diagram and the holes float up like bubbles.
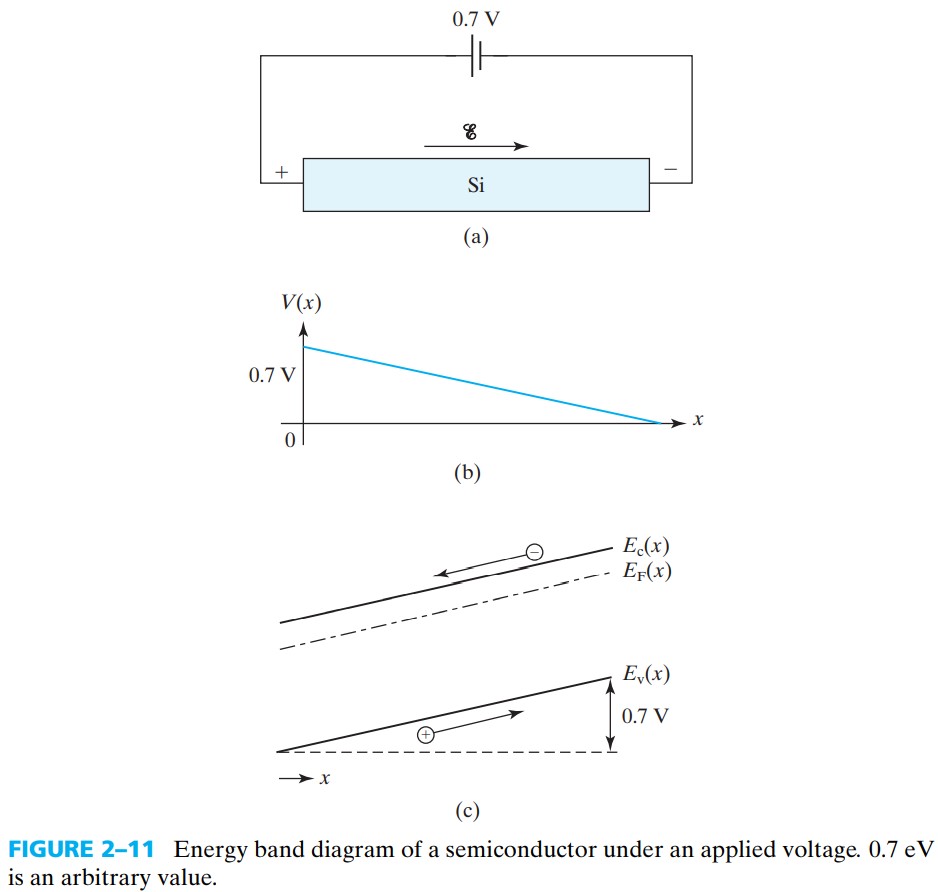
constant 的值由参考电位来决定,而由于 $E_c$ 的单位是 eV,所以 $V(x)$ 要乘上 $q$
对上式求导,我们可以得到:
$$ \mathscr{E}(x)=-\frac{\dif V}{\dif x}=\frac{1}{q} \frac{\dif E_c}{\dif x}=\frac{1}{q} \frac{\dif E_v}{\dif x} $$说明 $E_c,E_v$ 的斜率与外加电场成正比。
2.5 Einstein Relationship between D and μ
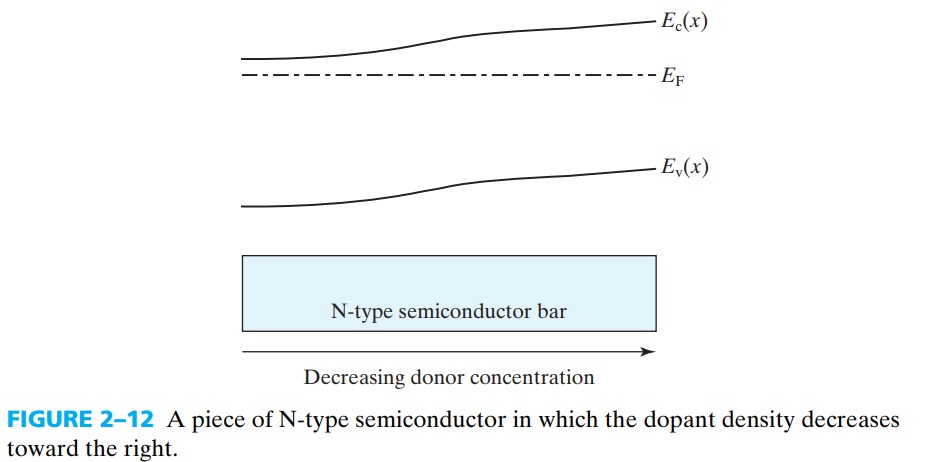
注意到 $D$ 与 $\mu$ 的含义很类似,都是载流子在某个外加条件下的运动能力。考虑在一个不均匀掺杂的半导体中(如图 fig 2-12),会产生扩散电流,而电流又会产生电场从而导致漂移电流,最终扩散电流会等于漂移电流,这样就能求出 $D$ 与 $\mu$ 的关系式。
将 $n = N_c e^{-(E_c-E_F)/kT}$ 和 $\dfrac{\dif E_c}{\dif x}=q\mathscr{E}$ 代入上式,有:
$$ 0 = q n \mu_n \mathscr{E} - qn\frac{qD_n}{kT} \mathscr{E}\\ \Rightarrow D_n = \frac{kT}{q} \mu_n \tag{2.5.6a} $$同理,这条关系式对空穴也成立:
$$ D_p = \frac{kT}{q}\mu_p \tag{2.5.6b} $$2.6 Electron-Hole Recombination
前面说的情况都是在平衡态下(equilibrium carrier concentrations)的情况, 某些情况下(比如光照),会产生过剩载流子 (excess carrier concentrations)。一般用 $n_0,p_0$ 表示平衡态,用 $n',p'$ 表示过剩:
$$ n'\equiv p' \tag{2.6.2}\\ n \equiv n_0 + n'\\ p \equiv p_0 + p' $$若停止光照,过剩载流子就会复合 (recombination),可以用 recombination time 或 carrier lifetime, $\tau$ 来描述复合所需的时间,定义式如下:
$$ \frac{\dif n'}{\dif t} = -\frac{n'}{\tau}=-\frac{p'}{\tau} $$复合速度与浓度有关(成正比)。我们可以这样理解上式,$n'$ 是路程,$\tau$ 是时间,$\frac{\dif n'}{\dif t}$ 是速度,那么 $\tau$ 描述的就是保持当前速度不变走完全程的时间。
recombination rate 结合律 为 $\dfrac{n'}{\tau}=\dfrac{p'}{\tau}$(单位:$/(\text{cm}^3\cdot s)$ )
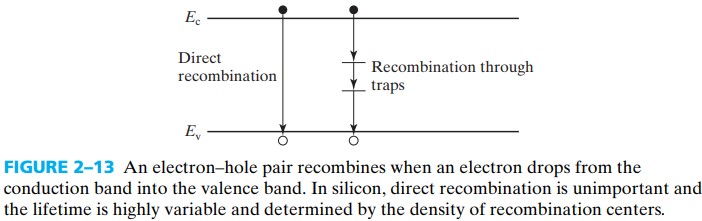
电子和空穴结合的方式有几种:
- 直接复合 direct recombination, or radiative recombination:导带电子与价带空穴直接结合
- direct gap semiconductors: efficient. used for light emission.
- indirect gap semiconductors: inefficient. the electrons and holes at the edges of the band gap do not have the same wave vectors
- 间接复合:导带电子与价带电子在 recombination centers 处复合
- 俄歇复合???
2.7 Thermal Generation
The reverse process of recombination is called thermal generation 热激发,显然,过剩载流子产生的速度等于 rate of generation minus rate of recombination
2.8 Quasi-Equilibrium and Quasi-Fermin Levels
前面说过,导带上的电子越多,费米能级就越高,而价带上的空穴越多,费米能级就越低。那么,当有过剩载流子时,电子和空穴都同时增多,此时,无法用单一费米能级来描述,于是定义了两个 quasi-Fermi levels, $E_{F_n}$ and $E_{F_p}$
$$ n = N_c e^{-(E_c-E_{F_n})/kT} \tag{2.8.1}\\ $$$$ p = N_v e^{-(E_{F_p}-E_v)/kT} \tag{2.8.2} $$这两个方程我们在后面还要用到。