统计量的分布

常用的抽样分布

以下分布是后续常见的分布，分别是 $\chi^2$分布，$t$分布，$F$ 分布。

$\chi^2$ 分布

$\chi^2$ 分布

设 $n$ 个随机变量 $X_1,X_2,\cdots,X_n$ 相互独立，都服从标准正态分布 $N(0,1)$，则称 $\chi^2=\sum_{i=1}^n X_i^2$ 服从自由度为 $n$ 的 $\chi^2$ 分布，记为 $\chi^2\sim\chi^2(n)$。（读作“卡方”分布）

自由度指 $\sum$ 包含的独立变量的个数

$\chi^2(n)$ 分布的概率密度为（不用记）：

$$ f_n(x)= \begin{cases} \frac{1}{2\Gamma(n/2)} \left( \frac{x}{2} \right)^{\frac{2}{n}-2}e^{-\frac{x}{2}} & x>0\\ 0 & x\leq 0 \end{cases}\\ \Gamma(\alpha)=\int_0^{+\infty} x^{\alpha-1} e^{-x} \dif x $$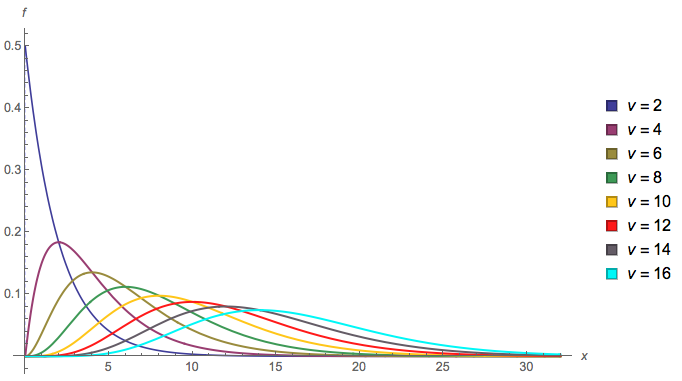

性质：

1. $E(\chi^2)=n$，$D(\chi^2)=2n$
2. 可加性：$Y_1\sim\chi^2(n_1)$，$Y_2\sim\chi^2(n_2)$，且 $Y_1,Y_2$ 相互独立，则 $Y_1+Y_2 \sim \chi^2(n_1+n_2)$

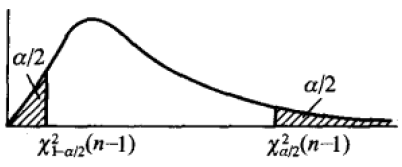
上 $\alpha$ 分位数

给定 $0< \alpha< 1$，称满足条件 $P(\chi^2>\chi^2\_\alpha(n))=\alpha$ 的点 $\chi_\alpha^2(n)$ 为 $\chi^2$ 分布的 上 $\alpha$ 分位数

可以通过查表找到不同自由度 $n$ 的上 $\alpha$ 分位数。

t 分布

t 分布

设 $X\sim N(0,1)$，$Y\sim \chi^2(n)$ ，且 $X,Y$ 相互独立，则称 $T=\dfrac{X}{\sqrt{Y/n}}$ 服从自由度为 $n$ 的 $t$分布，记为 $T\sim t(n)$ （也称为学生分布）

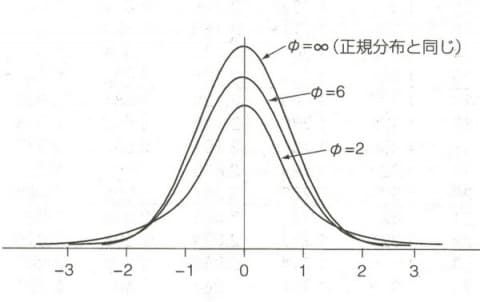
$t$ 分布的概率密度为（不用记）：

$$ f(x;n)=\frac{\Gamma(\frac{n+1}{2})}{\sqrt{n\pi}\Gamma(\frac{n}{2})} \left( 1+\frac{x^2}{n} \right)^{-\frac{n+1}{2}} $$

特别地，$n=1$ 的 $t$ 分布就是柯西分布：$f(x;1)=\frac{1}{\pi(1+x^2)}$；$n\rightarrow \infty$，$t$ 分布就是标准正态分布：$f(x;n)\rightarrow\frac{1}{\sqrt{2\pi}} e^{-x^2/2}$

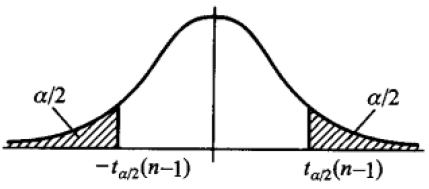
上 $\alpha$ 分位数

给定 $0< \alpha< 1$，称满足 $\int_{t_\alpha(n)}^\infty f(x;n)\dif x=\alpha$ 的点 $t_\alpha(n)$ 为 $t(n)$ 分布的 上 $\alpha$ 分位数

同样可查表得出。

[!TIP] 例题：$X\sim N(0, \sigma^2)$，$Y\sim N(0, \sigma^2)$，$X,Y$ 独立。取样 $(X_1,X_2,X_3,X_4)$ 和 $(Y_1,Y_2,Y_3,Y_4)$，构造 $U=\dfrac{X_1+X_2+X_3+X_4}{\sqrt{Y_1^2+Y_2^2+Y_3^2+Y_4^2}}$，问 $U$ 服从什么分布？

[!NOTE] 解：分子部分：

$$

X_1+X_2+X_3+X_4 \sim N(0,4\sigma^2)\ \frac{X_1+X_2+X_3+X_4}{2\sigma} \sim N(0,1) $$

分母部分：

$$ \frac{Y_i}{\sigma} \sim N(0,1)\\ \frac{1}{\sigma^2}(Y_1^2+Y_2^2+Y_3^2+Y_4^2) \sim \chi^2 (4) $$

$$ \frac{X_1+X_2+X_3+X_4}{2\sigma} \bigg/ \sqrt{\frac{1}{\sigma^2}(Y_1^2+Y_2^2+Y_3^2+Y_4^2)/4} \sim t(4)\\ 即 U=\dfrac{X_1+X_2+X_3+X_4}{\sqrt{Y_1^2+Y_2^2+Y_3^2+Y_4^2}} \sim t(4) $$

[!TIP] 例题：$X\sim N(0,\sigma^2)$，抽取样本 $X_1,X_2$，问 $\frac{X_1}{\vert X_2 \vert }$ 服从什么分布

[!NOTE] 解：分子部分：$X_1\sim N(0,\sigma^2)$，$\frac{X_1}{\sigma} \sim N(0,1)$
  分母部分：$X_2\sim N(0,\sigma^2)$，$\frac{X_2}{\sigma}\sim N(0,1)$
  $\frac{X_2^2}{\sigma^2} \sim \chi^2(1)$，$\dfrac{\frac{X_1}{\sigma}}{\sqrt{\frac{X_2^2}{\sigma^2}/1}} \sim t(1)$
  即 $\frac{X_1}{\vert X_2 \vert} \sim t(1)$

F 分布

F 分布

设 $X\sim\chi^2(n_1)$，$Y\sim\chi^2(n_2)$，且 $X,Y$ 独立，则称随机变量 $F=\dfrac{X/n_1}{Y/n_2}$ 服从自由度为 $(n_1,n_2)$ 的 F 分布，记作 $F\sim F(n_1,n_2)$

$n_1$ 是第一自由度，$n_2$ 是第二自由度

F 分布的倒数依然服从 F 分布，即 $\frac{1}{F}\sim F(n_2,n_1)$

F 分布的密度函数为（不用记）：

$$ \displaylines{ f(x;n_1,n_2)= \begin{cases} \frac{1}{B(n_1/2,n_2/2)} n_1^{n_1/2} n_2^{n_2/2} x^{n_1/2-1} (n_2+n_1 x)^{(n_1+n_2)/2} & x>0\\ 0 & x \leq 0\\ \end{cases}\\ B(a,b)=\int_0^1 x^{a-1} (1-x)^{b-1} \dif x } $$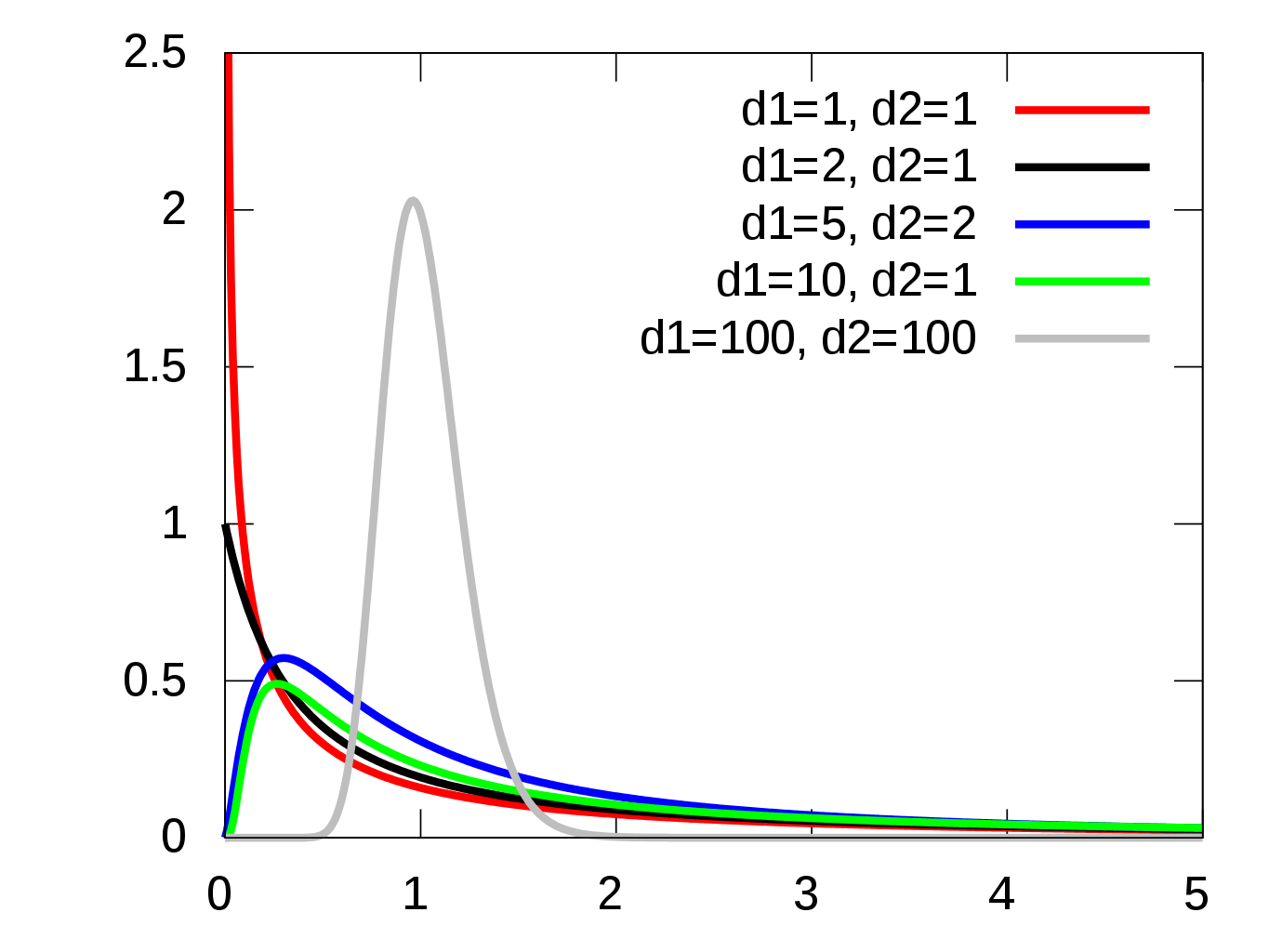

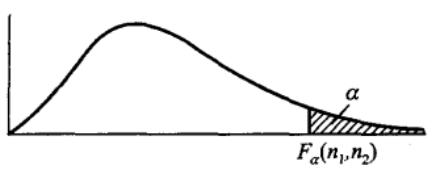
上 $\alpha$ 分位数

给定 $0< \alpha< 1$，称满足 $\int_{F_\alpha(n_1,n_2)}^\infty f(x;n_1,x_2)\dif x=\alpha$ 的点 $t_\alpha(n)$ 为 $t(n)$ 分布的 上 $\alpha$ 分位数

同样可查表得出。

查表可能用到的性质：$F_{1-\alpha}(n_1,n_2)=1/F_\alpha(n_2,n_1)$

[!TIP] 例题：已知 $X\sim t(n)$，求 $X^2\sim$ ?

[!NOTE] 解：$X\sim t(n)$，则存在 $U\sim N(0,1)$，$V \sim \chi^2(n)$，$U,V$ 独立，使得 $X = \frac{U}{\sqrt{V/n}}$
   $X^2 = \frac{U^2}{V/n}$
   $\because U \sim N(0,1)$，$\therefore U^2 \sim \chi^2(1)$
   $X^2=\frac{U^2/1}{V/n} \sim F(1,n)$

单个正态总体的抽样分布

请拉到下面看修改后的内容。

**📚定理一：**

设总体 $X\sim N(\mu,\sigma^2)$，$X_1,X_2,\cdots,X_n$ 是样本，样本均值 $\overline{X}=\frac{1}{n}\sum_{i=1}^n X_i$，样本方差 $S^2=\frac{1}{n-1}\sum_{i=1}^n (X_i-\overline{X})^2$，则：

1. $\overline{X} \sim N(\mu,\dfrac{\sigma^2}{n})$ ；建议记 $\dfrac{\overline{X}-\mu}{\sigma/\sqrt{n}} \sim N(0,1)$
2. $\dfrac{(n-1)S^2}{\sigma^2}\sim\chi^2(n-1)$
3. $\overline{X}$ 与 $S^2$ 相互独立。

🔍证明：

$$ E(\overline{X})=E(\frac{1}{n}\sum_{i=1}^n X_i)=\frac{1}{n} \sum_{i=1}^n E(X_i)=\mu\\ D(\overline{X})=D(\frac{1}{n}\sum_{i=1}^n X_i)=\frac{1}{n^2} \sum_{i=1}^n D(X_i)=\frac{\sigma^2}{n}\\ \because \overline{X} 是正态分布的线性组合\\ \therefore \overline{X}\sim N(\mu,\frac{\sigma^2}{n}) $$

第二个结论的证明很复杂，在此不给出。

[!TIP] 例题：设总体 $X\sim N(\mu,\sigma^2)$，$X_1,X_2,\cdots,X_n$ 是样本，求证

$$ \displaylines{ （1）\frac{\sum_{i=1}^n (X_i-\overline{X})^2}{\sigma^2}\sim\chi^2(n-1)\\ （2）\frac{\sum_{i=1}^n (X_i-\mu)^2}{\sigma^2}\sim\chi^2(n) } $$

Note

解：对于（1），因为有一个约束条件：$\sum_{i=1}^n (X_i-\overline{X})=0$，所以自由度为 $n-1$；而对于（2），这 $n$ 个随机变量之间相互独立，所以自由度为 $n$，$n$ 个标准正态分布的平方和服从 $\chi^2$ 分布。

请记住上面例题中的两个结论。（上面的公式 （1）其实就是定理一中的公式（2））

---

我们可以对定理一中的 $\overline{X}$ 进行标准化：

$$ \frac{\overline{X}-\mu}{\sigma/\sqrt{n}}\sim N(0,1) $$

如果不知道 $\sigma$，可以用 $S$ 来代替 $\sigma$，此时有：

📚定理二：

设总体 $X\sim N(\mu,\sigma^2)$，$X_1,X_2,\cdots,X_n$ 是样本，样本均值 $\overline{X}=\frac{1}{n}\sum_{i=1}^n X_i$，样本方差 $S^2=\frac{1}{n-1}\sum_{i=1}^n (X_i-\overline{X})^2$，则：

$$ \frac{\overline{X}-\mu}{S/\sqrt{n}}\sim t(n-1) $$

🔍证明：

$$ \frac{\overline{X}-\mu}{\sigma/\sqrt{n}}\sim N(0,1) \quad \dfrac{(n-1)S^2}{\sigma^2}\sim\chi^2(n-1)\\ \therefore \frac{\overline{X}-\mu}{S/\sqrt{n}} = \frac{\frac{\overline{X}-\mu}{\sigma/\sqrt{n}}}{\sqrt{\dfrac{(n-1)S^2}{\sigma^2}}}\sim t(n-1) $$

---

分割线（上面写的乱得一批，下面重新梳理过）

---

已知 $X\sim N(\mu,\sigma^2)$，从中抽取简单随机样本 $(X_1,X_2,\cdots,X_n)$，样本的统计量满足如下分布。

结论1{:.success}

$$ \begin{align*} &E(\overline{X})=E(\frac{1}{n}\sum_{i=1}^n X_i)=\frac{1}{n} \sum_{i=1}^n E(X_i)=\mu\\ &D(\overline{X})=D(\frac{1}{n}\sum_{i=1}^n X_i)=\frac{1}{n^2} \sum_{i=1}^n D(X_i)=\frac{\sigma^2}{n}\\ &\because \overline{X} 是正态分布的线性组合\\ &\therefore \overline{X}\sim N(\mu,\frac{\sigma^2}{n})\\ &标准化得到：\frac{\overline{X}-\mu}{\sigma/\sqrt{n}}\sim N(0,1) \end{align*} $$

结论2{:.success}

样本方差 $S^2 = \frac{1}{n-1} \sum_{i=1}^n (X_i-\overline{X})^2$ 应该与总体方差 $\sigma^2$ 相近，故作替换：

$$ \frac{\overline{X}-\mu}{S/\sqrt{n}}\sim t(n-1) $$

当 $n\rightarrow \infty$ 时，$S^2\Rightarrow \sigma^2$，$t(n-1) \Rightarrow N(0,1)$

结论3{:.success}

简单随机样本与总体同分布，故 $X_i \sim N(\mu,\sigma^2)$，标准化得到：$\dfrac{X_i-\mu}{\sigma} \sim N(0,1)$，根据 $\chi^2$ 分布的定义，有：

$$ \sum_{i=1}^n \left(\dfrac{X_i-\mu}{\sigma}\right)^2 \sim \chi^2(n)\\ 整理得到：\frac{\sum_{i=1}^n (X_i-\mu)^2}{\sigma^2}\sim\chi^2(n) $$

结论4{:.success}

总体均值为 $EX=\mu$，样本均值为 $\overline{X}=\frac{1}{n}\sum_{i=1}^n X_i$，这两者的值应该近似，故用样本均值替换结论3 中的总体均值，得到：

$$ \frac{1}{\sigma^2} \sum_{i=1}^n (X_i - \overline{X})^2 \sim \chi^2(n-1)\\ \Downarrow\\ \frac{n-1}{\sigma^2}\cdot\frac{1}{n-1}\cdot\sum_{i=1}^n (X_i - \overline{X})^2 \sim \chi^2(n-1)\\ \Downarrow\\ \frac{(n-1)S^2}{\sigma^2}\sim\chi^2(n-1) $$

因为存在约束条件：$\sum_{i=1}^n (X_i-\overline{X})=0$，故自由度少一个。

结论5{:.success}

$$ \frac{(n-1)S^2}{\sigma^2}\sim\chi^2(n-1)\\ \Rightarrow E [\frac{(n-1)S^2}{\sigma^2}] = n-1\\ \Rightarrow \frac{n-1}{\sigma^2} ES^2 = n-1\\ \Rightarrow ES^2 = \sigma^2 $$

注：这个结论不仅仅适用于正态总体，而是对于任意分布的总体，样本方差的均值都等于总体方差。

结论6{:.success}

$\overline{X}$ 与 $S^2$ 相互独立。

两个正态总体的抽样分布

设 $X_i,(i=1\cdots n_1)$ 和 $Y_j,(j=1\cdots n_2)$ 分别来自总体 $N(\mu,\sigma_1^2)$，$N(\mu_2,\sigma_2^2)$，并且它们相互独立。记样本均值为 $\overline{X},\overline{Y}$，样本方差为 $S_1^2,S_2^2$，则有：

定理1{:.success}

$$ F=\frac{S_1^2}{\sigma_1^2}\Big/\frac{S_2^2}{\sigma_2^2}=\frac{S_1^2}{S_2^2}\Big/\frac{\sigma_1^2}{\sigma_2^2}\sim F(n_1-1,n_2-1) $$

🔍证明：

$$ \because F=\dfrac{X/n_1}{Y/n_2} ,\; \dfrac{(n-1)S^2}{\sigma^2}\sim\chi^2(n-1)\\ \therefore F=\frac{S_1^2}{\sigma_1^2}\Big/\frac{S_2^2}{\sigma_2^2}=\frac{\chi_1^2/(n_1-1)}{\chi_2^2/(n_2-1)}\sim F(n_1-1,n_2-1) $$

定理2{:.success}

$$ \dfrac{(\overline{X}-\overline{Y})-(\mu_1-\mu_2)}{\sqrt{\dfrac{\sigma_1^2}{n_1}+\dfrac{\sigma_2^2}{n_2}}}\sim \mathrm{N}(0,1) $$

🔍证明：

$$ \overline{X}\sim N(\mu_1,\dfrac{\sigma_1^2}{n_1}),\; \overline{Y}\sim N(\mu_2,\dfrac{\sigma_2^2}{n_2})\\ \overline{X}-\overline{Y} \sim \mathrm{N}(\mu_1-\mu_2, \dfrac{\sigma_1^2}{n_1}+\dfrac{\sigma_2^2}{n_2})\\ 标准化后得证 $$

定理3{:.success}

$$ 当 \sigma_1=\sigma_2=\sigma 时，\\ \dfrac{(\overline{X}-\overline{Y})-(\mu_1-\mu_2)}{S_w\sqrt{\dfrac{1}{n_1}+\dfrac{1}{n_2}}}\sim \mathrm{t}(n_1+n_2-2)\\ S_w^2=\frac{(n_1-1)S_1^2+(n_2-1)S_2^2}{n_1+n_2-2} $$

🔍证明：

$$ \displaylines{ \dfrac{(\overline{X}-\overline{Y})-(\mu_1-\mu_2)}{\sqrt{\dfrac{\sigma_1^2}{n_1}+\dfrac{\sigma_2^2}{n_2}}}=\dfrac{(\overline{X}-\overline{Y})-(\mu_1-\mu_2)}{\sigma\sqrt{\dfrac{1}{n_1}+\dfrac{1}{n_2}}}\sim \mathrm{N}(0,1)\\ 而 \dfrac{(n_1-1)S_1^2}{\sigma_1^2}\sim\chi^2(n_1-1), \; \dfrac{(n_2-1)S_2^2}{\sigma_2^2}\sim\chi^2(n_2-1) 相互独立\\ \therefore \frac{(n_1-1)S_1^2+(n_2-1)S_2^2}{\sigma^2}\sim \chi^2(n_1+n_2-2)\\ 又： \overline{X} 与 S_1^2 ,\; \overline{Y} 与 S_2^2 相互独立，由 t分布的定义有：\\ \dfrac{(\overline{X}-\overline{Y})-(\mu_1-\mu_2)}{\sqrt{\dfrac{\sigma_1^2}{n_1}+\dfrac{\sigma_2^2}{n_2}}} \Bigg/ \frac{(n_1-1)S_1^2+(n_2-1)S_2^2}{\sigma^2}\\ =\dfrac{(\overline{X}-\overline{Y})-(\mu_1-\mu_2)}{S_w\sqrt{\dfrac{1}{n_1}+\dfrac{1}{n_2}}}\sim \mathrm{t}(n_1+n_2-2) } $$

为什么用 $S_w$ 不用 $S_1,S_2$：

---

6.2小结：

• 对于单个正态总体，得到了 $\overline{X},S^2$ 的分布，用于对 $\mu,\sigma$ 进行推断。
• 对于两个独立正态总体，得到了 $\overline{X}-\overline{Y}, S_1^2/S_2^2$ 的分布，用于对 $\mu_1-\mu_2,\sigma_1^2/\sigma_2^2$ 进行推断。

参考资料

分位数的图片取自：吴良超的学习笔记：概率论与数理统计知识整理(6)-参数估计，符合 CC BY 4.0 许可协议。