估计的评价标准
$$ \begin{align*} \newcommand{\dif}{\mathop{}\!\mathrm{d}} \newcommand{\p}{\partial} \newcommand{{\rm Cov}}{\text{Cov}}\\ \newcommand{\Mse}{\mathrm{Mse}} \end{align*} $$从上一节的几个例题中可以看出，矩估计和极大似然估计的估计量不同，那么如何选择估计量呢？这就涉及估计的评价准则。
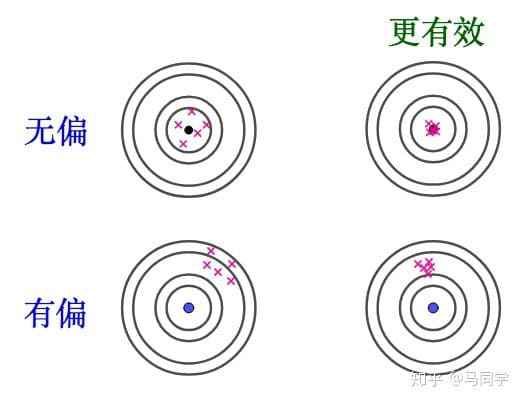
无偏性准则
定义{：success}
若参数 $\theta$ 的估计量 $\hat{\theta}=\hat{\theta}(X_1,X_2,\cdots,X_n)$ 满足 $E(\hat{\theta})=\theta$，则称 $\hat{\theta}$ 是 $\theta$ 的 无偏估计量。
若 $E(\hat{\theta})\neq \theta$，那么 $\vert E(\hat{\theta})-\theta \vert$ 称为估计量的 偏差
若 $\lim_{n\rightarrow \infty} E(\hat{\theta})=\theta$，则称 $\hat{\theta}$ 是 $\theta$ 的 渐近无偏估计量。
Tip
例题：设总体 $X$ 的一阶、二阶矩存在，$E(X)=\mu$，$D(X)=\sigma^2$
证明： 样本均值 $\overline{X}$ 和样本方差 $S^2$ 分别是 $\mu$ 和 $\sigma^2$ 的无偏估计；样本的2阶中心矩 $B_2$ 是 $\sigma$ 的渐进无偏估计。
$$ E(\overline{X})=E(\frac{1}{n} \sum_{i=1}^n X_i)=\frac{1}{n}\sum_{i=1}^n E(X_i)=\mu $$$$ E(S^2)=\sigma^2 $$$$ E(B_2)=\frac{n-1}{n} E(S^2)=\frac{n-1}{n}\sigma^2\\ \lim_{n\rightarrow \infty} E(B_2)=\sigma^2 $$
得证。 [!WARNING] 注：尽管 $B_2$ 不是无偏估计，我们可以通过纠偏，即乘上一个 $\frac{n}{n-1}$ 得到无偏估计。
补充：这里有道均匀分布的例题很重要。（复习时补上）
有效性准则
✒定义
设 $\hat{\theta}_1$ 和 $\hat{\theta}_2$ 是 $\theta$ 的两个无偏估计。如果 $D(\hat{\theta}_1)\leq D(\hat{\theta}_2)$ 对一切 $\theta$ 成立，并且不等号至少对某一 $\theta$ 成立，则称 $\hat{\theta}_1$ 比 $\hat{\theta}_2$ 有效。
补充：这里有道均匀分布的例题很重要。（复习时补上）
均方误差准则
✒定义
设 $\hat{\theta}$ 是参数 $\theta$ 的估计，方差存在，则称 $E(\hat{\theta}-\theta)^2$ 是估计量 $\hat{\theta}$ 的 均方误差，记为 $\Mse(\hat{\theta})$. 若 $\hat{\theta}$ 是无偏估计，则有 $\Mse(\hat{\theta})=D(\hat{\theta})$