一元离散随机变量

随机变量

前面我们的事件分为两类：数值的和非数值的（数值：扔骰子；非数值：是否射中）。对于非数值的，我们为了方便研究，也把它看作数值的，所以我们定义随机变量。

✒定义

随机变量

定义在样本空间 $\Omega$ 上的实函数 $X=X(\omega), \omega\in\Omega$。$X$ 称为随机变量，一般简记为 $X$，是一个从样本空间到实数的映射。

随机事件可以用随机变量表示为 $A=\{e:X(e)\in I\}=\{X\in I\}$ $I\in\mathbb{R}$，即随机事件对应于某个范围的随机变量

📝注释

1. 对于 $i\neq j$，必有 $\{X=i\}\cap\{X=j\}=\varnothing$
2. 允许出现多个事件对应一个随机变量
3. 一般用大写字母 $X、Y、Z$ 或希腊字母 $\xi, \eta$ 来表示随机变量

分布函数

分布函数

设 $X$ 是一个随机变量，$x$ 是任意实数，函数 $F(x)=P\{\omega | X(\omega)\leq x\}$ 称为随机变量 $x$ 的分布函数，记作 $F_X(x)$ 或 $F(x)$，有时也简记为 $F_X(x)=P\{X\leq x\}$。

该定义适用于连续随机变量和离散随机变量。

分布函数给出了随机变量落入任意一个范围的可能性。

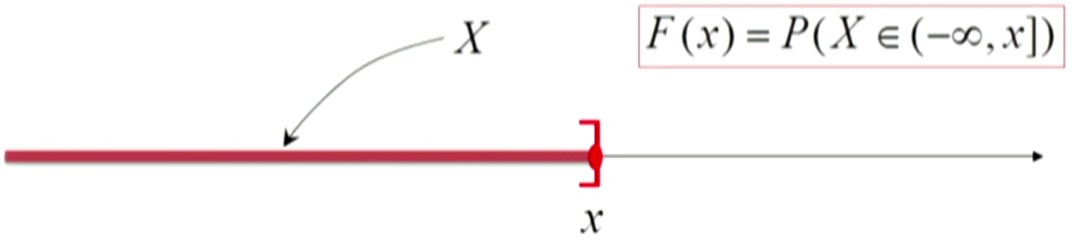
对于 $\forall a< b$，可以用分布函数表达如下概率：

1. $P(X< a)=F(a-0)$
2. $P(X=a)=F(a)-F(a-0)$
3. $P(a< X\leq b)==P(X \leq b) - P(X \leq a)=F(b)-F(a)$
4. $P(a\leq X \leq b)=P(X\leq b) - P(X< a)=F(b)-F(a-0)$

$$ F(X)=P(X\leq x)= \begin{cases} 0, x<1\\ 1/6, 1\leq x<2\\ 1/2, 2\leq x<3\\ 1, x\geq3 \end{cases} $$

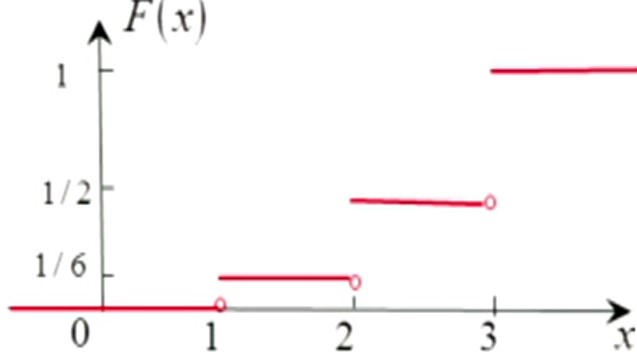
利用上图解释一下 $F(x-0)$ 和 $F(x+0)$ 的不同。对于连续点，$F(x-0)=F(x+0)$；对于非连续点，比如上图中，$x=1$，则 $F(1-0)=0\neq F(1)$，$P(1+0)=1/6 = F(1)$ （右连续）

分布函数的性质：

1. $F(x)$ 是单调增函数

   $$ \begin{aligned} &\because \forall x_1\leq x_2, 有 0\leq P(x_1< X\leq x_2)=F(x_2)-F(x_1)\\ &\therefore F(x_1)\leq F(x_2) \end{aligned} $$

2. $0\leq F(X)\leq1$

3. $F(x_0+0)=F(x_0)$，其中 $F(x_0+0)=\lim_{x\rightarrow x_0^+} F(x)$。相应的，函数图中，间断点的右边为实心点，左边为空心点（如上图）

   注意，以上表示满足 右连续，但不满足左连续，这与分布函数定义中的 $F_X(x)=P\{X\leq x\}$ 有关。在有的教科书中，$F_X(x)=P\{ X\leq x \}$，则满足左连续不满足右连续。

对于满足以上性质的函数都可以看作分布函数。

[!TIP] $F_1(x), F_2(x)$ 是两个分布函数，问 $F_1(x)\cdot F_2(x)$，$F_1(x)+F_2(x)$ 是否是分布函数？

[!NOTE] $F_1(x)\cdot F_2(x)$是，而$F_1(x)+F_2(x)$，因为后者不满足第2条性质。

[!TIP] 例题：设一个醉汉游离于 A,B 两点，AB之间距离为3个单位，该醉汉停在AB间任一子区间的概率于区间长度成正比，设他落在离 A 点距离 $X$ 远处，求 $X$ 的分布函数。

[!NOTE] 解：
  由题意，$P(0\leq X \leq 3)=1$
  故当$x<0$时，$F(x)=0$，当$X\geq3$时，$F(x)=1$
  设比例系数为k，则 $P(0\leq X \leq 3)=3k=1$，得 $k=1/3$
  当 $0\leq X<3$时，$F(x)=P(X\leq x)$$=P(X<0)+P(0\leq X\leq x)=0+\frac{1}{3}x$
  从而分布函数为：
$$ F(x)=P(X\leq x) \begin{cases} 0, x<0\ x/3, 0\leq x\leq3\ 1, x\geq3 \end{cases}

$$

离散型随机变量

✒定义 离散型随机变量

若随机变量的取值为有限个或可数个¹，则称 $X$ 为离散型随机变量。

分布律

离散型随机变量的概率分布律就是一个表格，表格包含：

1. 随机变量的所有可能取值
2. 每个取值的概率（$p_k\geq 0$，$\sum_k p_k=1$）

除了表格外，有时也用 $P(X=x_k)=p_k$ 来表示。

分布律与分布函数之间的转换：分布律的每个 $X$ 值对应分布函数的间断点 $x$，$P$ 对应间断点处的值减上一间断点的值。

X 1 2 3 P 1/6 1/3 1/2

二项分布

如果一个随机变量 $X$ 取值为 $0,1,2,\cdots,n$，且 $P(X=k)=C_n^k p^k （1-p）^{n-k}$，$k=0,1,2,\cdots,n$，则 $X$ 称为二项分布（Binomial），记为 $X\sim B(n,p)$

（也可定义为：n重贝努里实验²中，事件A 出现的次数 X 服从二项分布）

特殊地，

1. 如果 $n=1$，则称为两点分布（01分布），其分布律满足 $P(X=k)=p^k(1-p)^{1-k}, k=0,1$
2. 如果随机变量 $X$ 只取常数，则称 $X$ 为退化分布（单点分布），其分布律满足 $P(X=c)=1$

✒️定理：

若 $X\sim B(n,p)$，则由下式成立：

1. 事件A发生的次数在 k1，k2 之间：$P(k_1\leq X \leq k_2)=\sum_{k=k_1}^{k_2}B(k;n,p)$
2. 事件A发生的次数至少为 r 的概率，$P(X\geq r)=1-\sum_{k=0}^{r-1}B(k;n,p)$

✒️定理：

设 $X\sim B(n,p)$，令 $m=\text{Int}[(n+1)p]$

则 $k=m$ 时，$B(k;n,p)$ 的值最大，并且有 $B(k;n,p)=B(k-1;n,p)$

🔍证明：

$$ 令 r=\frac{b(k;n,p)}{b(k-1;n,p)}\\ 则 $$

泊松分布

若离散型随机变量 $X$ 的分布律为：$P(X=k)=\frac{\lambda^k}{k!}e^{-\lambda}$，$k=0,1,2,\cdots$，其中 $\lambda\geq0$ 是常数。称这分布为 泊松分布（Poisson），记为 $X\sim\text{Pois}(\lambda)$

🚩注意请记住这条泰勒展式：$e^\lambda=\sum_{k=0}^{+\infty} \dfrac{\lambda^k}{k!}$，后面会经常用到。

✒️定理： 泊松定理

当 $n>10$，$p<0.1$ 时，二项分布 $X\sim B(n,p)$ 可以用泊松分布 $X\sim \text{Pois}(np)$ 近似，即：

$$ C_n^kp^k(1-p)^{n-k}\approx\frac{e^{-\lambda}\lambda^k}{k!}, 其中, \lambda\approx np $$

几何分布

若 $X$ 满足 $P(X=k)=p(1-p)^{k-1}$，$k=1,2,3,\cdots$，其中 $0几何分布（Geometric），记为 $X\sim \text{Geom}(p)$ 或 $X \sim G(p)$

几何分布的用途：在n重贝努里实验中，实验进行到某种结果出现第一次为止，此时的实验总次数服从几何分布。

---

以上列出的分布要熟记。