全概率公式与贝叶斯公式
全概率公式
- 全概率公式(Total Probability Theorem)
- 设 $A_1, A_2, \cdots, A_n$ 满足:
- (1)$A_1, A_2, \cdots, A_n$ 两两互斥
- (2)$\sum_{i=1}^n A_i= \Omega$(互斥完备群)
- (3)$P(A_i)>0 \;(i=1,2,\cdots,n)$
- 则对任一事件 B,都有 $P(B) = \sum_{i=1}^n P(A_i)P(B \vert A_i)$,称为 全概率公式
🔍证明:
$$ \begin{align} \because B &= B\Omega = B(A_1 \cup A_2 \cup \cdots \cup A_n)\\ &= BA_1 \cup BA_2 \cup \cdots \cup BA_n \end{align}\\ \text{由条件}P(A_i)>0 \text{,且} (BA_i)(BA_j)=\varnothing \text{所以有}\\ P(B) = P(BA_1) + P(BA_2)+\cdots+P(BA_n)\\ =P(A_1)P(B|A_1)+\cdots+P(A_n)P(B|A_n) $$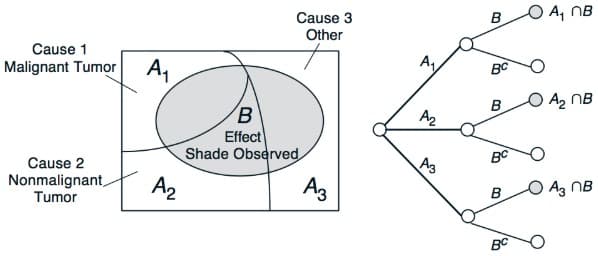
贝叶斯公式
- 贝叶斯公式(Bayes Rule)
- 设 $A_1, A_2, \cdots, A_n$ 两两互斥,且
- (1)$\sum_{i=1}^n A_i= \Omega$(互斥完备群)
- (2)$P(B)>0,\; P(A_i)>0 \;(i=1,2,\cdots,n)$
- 则有 $P(A_i\vert B) = \frac{P(A_iB)}{P(B)} = \frac{P(B\vert A_i)P(A_i)}{\sum_{i=1}^n P(A_i)P(B \vert A_i)}$,称为 贝叶斯公式,其中,称 $P(B\vert A_i)$ 为先验概率,$P(A_i\vert B)$ 为后验概率。
习题
全概率公式与贝叶斯公式相关的问题的特点是“二阶段性”。已知前一阶段的概率,求后一阶段,则用全概率公式;已知后一阶段,求前一阶段,则用贝叶斯公式。一般题目给出概率的,或概率比较好求的,作为前一阶段,并建立互斥完备群。
Tip
一小学举办家长开放日,欢迎家长参加活动,小明的母亲参加的概率为80%。若母亲参加,则父亲参加的概率为30%,若母亲不参加,则父亲参加的概率为90%。
(1)求父母都参加的概率
(2)求父亲参加的概率
(3)已知父亲参加的情况下,母亲参加的概率
Note
解:设 A={母亲参加},B={父亲参加}
由题意$P(A)=0.8, P(B|A)=0.3, P(B|\bar{A})=0.9$
(1)$P(AB)=P(A)P(B|A)=0.24$
(2)由全概率公式:$P(B)=P(A)P(B|A)+P(\bar{A})P(B|\bar{A})$$=0.8\times0.3+0.2\times0.9=0.42$
(3)由贝叶斯公式:$P(A|B)=\frac{P(AB)}{P(B)}=\frac{P(A)P(B|A)}{P(B)}=\frac{4}{7}$
Tip
某种诊断癌症的试验具有5%的假阳性,以及3%的假阴性,即:若设 A={试验反应是阳性},B={被诊断患有癌症},则有:
$$ P(A|\bar{C})=5\%,\;P(\bar{A}|C)=3\% $$已知某一群体 $P(C)=0.005$,问这种方法能否用于普查?
[!NOTE]
解: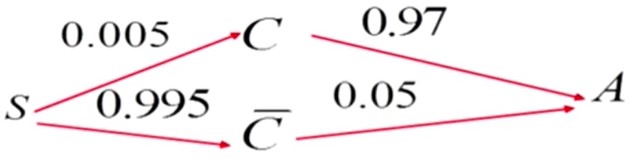
由贝叶斯公式:
$$ P(C|A)=\frac{P(CA)}{P(A)}=\frac{P(C)P(A|C)}{P(C)P(A|C)+P(\bar{C})P(A|\bar{C})}=0.089 $$说明,在被检测出阳性的人群中,仅有8.9%的人为患有癌症。所以该方法不适用于普查。
Caution
补充:若 P(C) 比较大,比如 $P(C)=0.8$,则根据上面的公式,计算出 $P(C|A)=0.987$,所以该方法适用于肿瘤医院使用。
补充