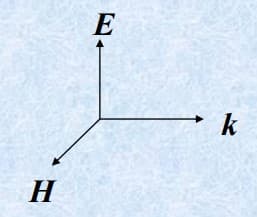
平面电磁波
$$ \begin{align*} \newcommand{\dif}{\mathop{}\!\mathrm{d}}\\ \newcommand{\p}{\partial}\\ \newcommand{\bd}{\boldsymbol}\\ \newcommand{\E}{\mathscr{E}}\\ \newcommand{\db}[1]{\dot{\boldsymbol{#1}}} \end{align*} $$平面波与均匀平面波
- 等相位面（波阵面）
- 空间相位相同的点构成的面
- 根据波振面的形状可以分成：平面波、柱面波、球面波
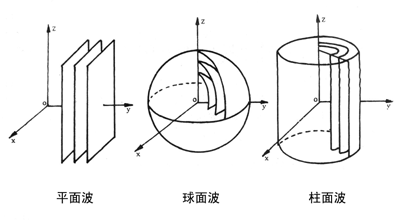
- 均匀平面波（UPW）
- 等相位面上的电场、磁场各点的振幅相同
- 均匀平面波：$\bd{E}=\hat{a}_x E_0\cos(\omega t - kz)$，非均匀平面波：$\bd{E}=\hat{a}\_\theta \frac{E_0}{r}\sin\theta\cos(\omega t - kr)$
下面来写一下均匀平面波的表达式。设 UPW 的传播方向为 $+z$ 方向，按照定义，幅度只与 $z$ 有关：
$$ \db{E}=\db{E}(z) \quad \db{H}=\db{H}(z) $$对应的亥姆霍兹方程：
$$ \nabla^2 \db{E}(z)+k^2 \db{E}(z)=0\\ \begin{cases} \frac{\p \dot{E}_x(z)}{\p z^2}+k^2 \dot{E}_x(z)=0\\ \frac{\p \dot{E}_y(z)}{\p z^2}+k^2 \dot{E}_y(z)=0\\ \frac{\p \dot{E}_z(z)}{\p z^2}+k^2 \dot{E}_z(z)=0\\ \end{cases}\\ 解得\Rightarrow \begin{cases} \db{E}_x=E_{mx} e^{-jkz}\\ \db{E}_y=E_{my} e^{-jkz}\\ \db{E}_z=E_{mz} e^{-jkz} \end{cases}\\ \Rightarrow \db{E}=(\hat{a}_x E_{mx}+\hat{a}_y E_{mx}+\hat{a}_z E_{mx})e^{-jkz}=\bd{E}_0 e^{-jkz} $$根据无源区的电场散度：$\nabla\cdot\db{D}=\varepsilon \nabla\cdot\db{E}=0$，将 $\db{E}$ 代入：
$$ \nabla\cdot (\bd{E}_0 e^{-jkz} )=0\\ e^{-jkz}\nabla\cdot \bd{E}_0+\bd{E}_0\cdot\nabla e^{-jkz}=0\\ $$第一项 $\bd{E}_0$ 是常矢量，所以散度为 0；而第二项：
$$ \bd{E}_0 \cdot \hat{a}_z(-jk)e^{-jkz}=0\\ \Rightarrow \bd{E}_0 \cdot \hat{a}_z=0 $$上式说明：电场方向（$\bd{E}_0$）与传播方向（$\hat{a}_z$）垂直
设电场方向为 x 方向，则 $\db{E}=\hat{a}_x \dot{E}_x(z)=\hat{a}_x E_m e^{-jkz}$
根据无源区的Maxwell方程（$\bd{J}=0\; \rho=0$）：
$$ \begin{cases} \nabla\times\db{E}=-j\omega\mu\db{H}\\ \nabla\times\db{H}=j\omega\varepsilon \db{E} \end{cases}\\ \Rightarrow \begin{cases} -jk \hat{a}_z \times\db{E}=-j\omega\mu\db{H}\\ -jk \hat{a}_z\times\db{H}=j\omega\varepsilon \db{E} \end{cases}\\ \Rightarrow \begin{cases} \db{H}=\frac{k}{\omega\mu}\hat{a}_z \times \db{E}\\ \db{E}=-\frac{k}{\omega\mu}\hat{a}_z \times \db{H} \end{cases} $$总结上面一系列的内容：
$$ \begin{cases} \db{H}=\frac{k}{\omega\mu}\hat{a}_z \times \db{E}\\ \db{E}=-\frac{k}{\omega\mu}\hat{a}_z \times \db{H} \end{cases} $$
可以求得：$\db{H}=\frac{k}{\omega\mu} \hat{a}_z \times \db{E}=\hat{a}_y \frac{k}{\omega\mu} \db{H}_y(z)$，时域表达式为 $H_y(z,t)=\frac{k}{\omega\mu} E_m \cos (\omega t - kz)$
重要参数
表达式 $E_x(z,t)=E_m \cos (\omega t - kz)$ 中，$\omega t$ 是时间相位，$k z$ 是空间相位，有下面几个参数：
- 周期：时间相位变化 $2\pi$，$\omega t=2\pi$，即 $T=2\pi/\omega$
- 波长：空间相位变化 $2\pi$，$k z=2\pi$，即 $\lambda=2\pi/k$
此外，还有：
- 波数 $\beta$：每单位距离改变的相位
- 无耗媒质中 $\beta=k=\omega\sqrt{\mu\varepsilon}=\dfrac{\omega}{v}$$=\dfrac{2\pi}{Tv}=\dfrac{2\pi}{\lambda}$
- 有耗媒质中：（待写）
- 相速 $v_p$：无耗媒质中，波阵面推进的速度 $$ \omega t - kz=\mathrm{const}\\ v_p=\frac{\dif z}{\dif t}=\frac{\omega}{k}=\frac{\omega}{\beta}=\frac{1}{\mu\varepsilon}=\lambda f $$
做题中常需要参数互求，所以上面的公式需要牢牢记住。
传播特性
上面都是数学推导，下面来说说从公式中能读出什么。
$$ E_x(z,t)=E_m \cos (\omega t - kz)\\ H_y(z,t)=\frac{k}{\omega\mu} E_m \cos (\omega t - kz) $$电场、磁场在空间中相互垂直 $\bd{E}\cdot\bd{H}=0$，且波形相同，时间同相；
电场、磁场的模值比是只与媒体特性有关的常数，定义为 本征阻抗（波阻抗）$\eta$
$$ \eta=\frac{E_x}{H_y}=\frac{\omega\mu}{k}=\sqrt{\frac{\mu}{\varepsilon}}\\ =\sqrt{\frac{\mu_r \mu_0}{\varepsilon_r \varepsilon_0}}=\eta_0 \sqrt{\frac{\mu_r}{\varepsilon_r}} $$$\mu_0$ 为真空波阻抗，$\mu_0=120\pi=377 \rm{\Omega}$
电场、磁场与能流方向垂直，这种波叫 横电磁波 TEM（Transverse Electric and Magnetic）
$$ \bd{S}(t)=\bd{E}(s)\times\bd{H}(t)=\hat{a}_x E_x \times \hat{a}_y H_y=\hat{z}E_xH_y\\ \bd{S}_{平均}=\hat{a}_z \frac{1}{2\eta} |\dot{E}_x|^2=\hat{a}_z \frac{1}{2}\eta |\dot{H}_y|^2 $$电场、磁场在空间任意点的能量密度相等
$$ \frac{1}{2}\mu H_y^2=\frac{1}{2}\mu \left( \frac{E_x}{\eta} \right)=\frac{1}{2} \frac{\mu}{\mu_\varepsilon} E_x^2=\frac{1}{2}\varepsilon E_x^2 $$说明空间中只有能量流动，没有能量交换
能速 $v_e=S(t)/(w_e+w_m)$，在均匀理想介质（真空）中，$v_e=\dfrac{1}{\mu\varepsilon}=v_p$
波矢量
将 $+z$ 方向改为任意方向：$\db{E}=\bd{E}_0 e^{-jk\xi}$，而 $\xi= \hat{a}\_\xi\cdot \bd{r}$，代入得：$\db{E}=\bd{E}_0 e^{-jk\hat{a}\_\xi\cdot \bd{r}}$
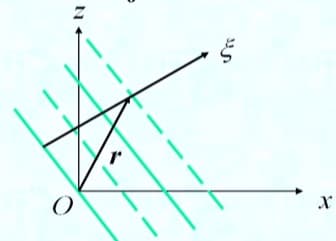
考虑指数部分：$-jk\hat{a}_\xi\cdot \bd{r}$，我们令 $\bd{k}=k\hat{a}\_\xi$，定义为 波矢量。其大小为相移常数（无耗介质中的波数），方向为波传播方向。
从而波的数学表达式：
$$ \db{E}=\bd{E}_0 e^{-j\bd{k}\cdot\bd{r}}\\ \bd{E}(\bd{r},t)=\bd{E}_0\cos(\omega t-\bd{k}\cdot\bd{r}) $$相应的，我们将之前讲过的内容用 $\bd{k}$ 替换：
$$ \bd{k}\cdot \bd{E}=0\\ \bd{k}\cdot \bd{E}=0\\ \bd{E}\cdot \bd{H}=0\\ \hat{a}_E\times\hat{a}_H=\hat{a}_k\\ \left| \frac{\bd{E}}{\bd{H}} \right|=\eta=\sqrt{\frac{\mu}{\varepsilon}}\\ \bd{H}(\bd{r})=\frac{1}{\eta}\hat{a}_k \times \bd{E}(r)\\ \bd{E}(\bd{r})=\eta \bd{H}(\bd{r})\times\bd{a}_k $$实际上就是要记住$\bd{E,H,k}$ 之间的叉乘关系（下图）。
