边界条件
$$ \begin{align*} \newcommand{\dif}{\mathop{}\!\mathrm{d}}\\ \newcommand{\p}{\partial}\\ \newcommand{\bd}{\boldsymbol}\\ \newcommand{\E}{\mathscr{E}} \end{align*} $$由于麦克思维方程组的微分形式在不同媒质的分界面上不成立(不连续),所以只能用积分形式来推导。
$$ \begin{cases} \oint_C \bd{H}\cdot\dif\bd{l}=\int_S \bd{J}\cdot \dif \bd{S}+\int_S \frac{\p \bd{D}}{\p t} \cdot \dif \bd{S}\\ \oint_C \bd{E}\cdot\dif\bd{l}=-\int_S \frac{\p \bd{E}}{\p t} \cdot \dif \bd{S}\\ \oint_S \bd{B} \cdot \dif \bd{S} = 0\\ \oint_S \bd{D}\cdot \dif \bd{S}=q \end{cases} $$切向磁场分量
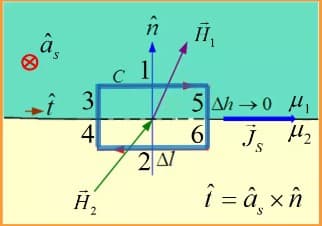
对磁场进行线积分,有:
$$ \oint_C \bd{H} \cdot \dif \bd{l}=\bd{H}_1 \cdot \hat{t}\Delta l- \bd{H}_2 \cdot \hat{t} \Delta l=I_C+I_D\\ \begin{align*} I_C&=\int_S \bd{J}\cdot\dif \bd{S}=\bd{J}_S\cdot\hat{a}_S \Delta l\\ I_D&=\int_S \frac{\p \bd{D}}{\p t} \cdot \dif S=\lim_{\Delta h\rightarrow 0} \frac{\p \bd{D}}{\p t}\cdot \hat{a}_S \Delta h \Delta l=0 \end{align*}\\ \therefore \hat{n}\times(\bd{H}_1-\bd{H}_2)=\bd{J}_S $$总结如下:切向电场强度与法向磁感应强度连续,法向电位移和切向磁场强度不连续。
$$ \begin{cases} H_{1t}-H_{2t}=J_s\\ E_{1t}-E_{2t}=0\\ B_{1n}-B_{2n}=0\\ D_{1n}-D_{2n}=\rho_S \end{cases}\\ (从2指向1) $$对于理想导体($\sigma\rightarrow\infty$),$\bd{E}=0$,$\bd{B}=0$。我们把导体看作媒质2,则有:
$$ \begin{cases} \hat{n}\cdot \bd{D}=\rho_S\\ \hat{n}\times\bd{D}=\bd{J}_S \end{cases} $$上式说明:
- 理想导体表面切向电场和法向磁场为零;
- 电场总垂直与导体表面
(例 5-2-1)
波动方程
场量 $u$ 的波动方程标准形式为:
$$ \nabla^2 u -\frac{1}{v^2} \frac{\p^2 u}{\p t^2}=-g $$$v$ 是波速,$t$ 是时间,$g$ 是源。波动方程的解为以速度 $v$ 传播的波。
下面用麦克斯韦方程组导出电磁场的波动方程:
设媒质均匀、线性、各向同性,对麦克斯韦方程组的第一、第二方程求导数:
$$ \begin{align} \nabla\times\nabla\times\bd{H}&=\nabla\times\bd{J}+\nabla\times\frac{\p\bd{D}}{\p t}\\ &=\nabla\times\bd{J}+\frac{\p \nabla\times\bd{D}}{\p t}\\ &=\nabla\times\bd{J}+\varepsilon \frac{\p \nabla\times\bd{E}}{\p t}\\ &=\nabla\times\bd{J}+\varepsilon\frac{\p\bd{B}}{\p t} \\ &=\nabla\times\bd{J}+\varepsilon\mu \frac{\p\bd{H}}{\p t} \end{align} $$而 $\nabla\times\nabla\bd{F}=\nabla(\nabla\cdot\bd{F})-\nabla^2 \bd{F}$
所以:
$$ \begin{cases} \nabla^2 \bd{H}-\mu\varepsilon \frac{\p^2 \bd{H}}{\p t^2}=-\nabla\times\bd{J} \end{cases} $$