磁偶极子与磁介质
$$ \begin{align*} \newcommand{\dif}{\mathop{}\!\mathrm{d}}\\ \newcommand{\p}{\partial}\\ \newcommand{\bd}{\boldsymbol} \end{align*} $$磁偶极子
我们将线度很小(也就是大小很小)的电流环称为 磁偶极子。假设其具有恒定电流 $I$,半径为 $a$,面积为 $\bd{S}$(与电流方向成右手螺旋关系),那么其磁偶极矩为:$\bd{p}_m=I\bd{S}$
下面我们考虑通有电流 $I$ 半径 $a$ 的小圆环在远离圆环处的磁场强度。此时圆环可以视作一个点,所以以圆环为 $\varphi$ 平面,建立球坐标系。
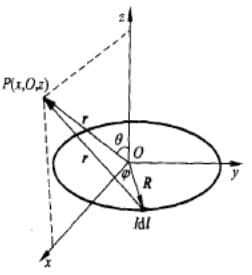
由于场分布具有轴对称性,所以我们只需考虑 $P(r,\theta,0)$ 处的磁场。此处,线元 $I\dif \bd{l}$ 产生的磁矢位为:
$$ \dif \bd{A}=\frac{\mu_0}{4\pi} \frac{I\dif \bd{l}'}{R}\\ (R为电流源到场点的距离) $$我们在 $x$ 轴另一侧选取对称的电流元,这一对电流元的叠加的磁矢位,在 $x$ 方向相消,只在 $y$ 方向不为0,大小为:
$$ 2\dif A \cos \varphi = \frac{\mu_0 I}{4\pi R} a \dif \varphi \cdot 2\cos\varphi $$我们利用几何关系,将 $R$ 表示出来:
$$ \begin{align} R&=[(r\cos\theta^2)^2 + (a\sin\varphi)^2+(r\sin\theta-a\cos\varphi)^2]^{1/2}\\ &=r(1+\frac{a^2}{r^2}-\frac{2a}{r}\sin\theta\cos\varphi)^{1/2} \end{align} $$$$ \begin{align} &\because r \gg a\\ &\therefore \frac{1}{R}\approx\frac{1}{r} (1+\frac{a}{r}\sin\theta\cos\varphi) \end{align} $$从而对电流元积分得到:
$$ \begin{align} A_\varphi(r,\theta)&=\frac{\mu_0Ia}{2\pi r}\int_0^\pi (1+\frac{a}{r}\sin\theta\cos\varphi)\cos \varphi \dif \varphi\\ &=\frac{\mu_0Ia}{2\pi r} \cdot \frac{a}{r} \sin\theta \cdot \frac{\pi}{2}\\ &=\frac{\mu_0 IS \sin\theta}{4\pi r^2}\\ \bd{A}(r,\theta)&= \frac{\mu_0 IS \sin\theta}{4\pi r^2} \bd{a}_\varphi \end{align} $$从而磁场强度为:
$$ \bd{B}=\nabla\times \bd{A} \approx \frac{\mu_0 SI}{4\pi r^3}(\bd{a}_r 2\cos\theta + \bd{a}_\theta \sin\theta)\\ \bd{E}\approx \frac{p}{4\pi\varepsilon_0 r^3 }(\bd{a}_r 2\cos\theta + \bd{a}_\theta \sin\theta) $$从式子中可以看出,电偶极子和磁偶极子具有对偶性。
对磁偶极子的磁矢位进行推广:
$$ \begin{align} \bd{A}(r,\theta)&= \frac{\mu_0 IS \sin\theta}{4\pi r^2} \bd{a}_\varphi\\ &= \frac{\mu_0}{4\pi} \cdot IS \cdot \bd{a}_z \times \frac{\bd{r}}{r^3}\\ &=\frac{\mu_0}{4\pi} \bd{p}_m \times (\nabla\frac{1}{r}) \end{align} $$$p_m=IS$ 称为磁偶极距。
磁化
电子自旋(自旋磁矩)与电子绕核运动(轨道磁矩)使得分子具有分子磁矩 $p_m=I_sS_i$。由于热运动,分子磁矩相互抵消,所以物质不显示磁性。但在外加磁场作用下,分子重新排列,会 磁化 产生新的磁场。根据磁化特点,分为:
- 抗磁性(水、铜、有机物):产生的磁场与外加磁场相反($\mu< \mu_0$)
- 顺磁性(锂、钠、铝、氧气):产生的磁场与外加磁场相同,磁性较弱($\mu>\mu_0$)
- 铁磁性(铁、钴、镍、钆):产生的磁场与外加磁场相同,磁性很强,甚至会大于原有磁场,有磁畴
- 亚铁磁性物质
- 磁化强度
- 单位体积中,磁矩矢量和称为磁化强度:
- $\bd{M}=\lim_{\Delta V\rightarrow0} \frac{\sum_{i=1}^{n}\bd{p}_{mi}}{\Delta V}\;\rm{(A/m)}$
媒质被磁化后,总的矢量磁位为:
$$ \begin{align} \bd{A}(\bd{r})&=\frac{\mu_0}{4\pi}\int_{V'} \frac{\bd{M}\times\bd{R}}{R^3} \dif V'\\ &=\frac{\mu_0}{4\pi}\int_{V'} \bd{M}\times\nabla' \left(\frac{\bd{R}}{R^3}\right) \dif V'\\ &=\frac{\mu_0}{4\pi}\int_{V'} \frac{\nabla'\times \bd{M}}{R}\dif V' - \frac{\mu_0}{4\pi}\int_{V'} \nabla \times \left( \frac{\bd{M}}{R} \right) \dif V'\\ &=\frac{\mu_0}{4\pi}\int_{V'} \frac{\nabla'\times \bd{M}}{R}\dif V' + \frac{\mu_0}{4\pi}\int_{S'} \frac{\bd{M}\times \bd{n}}{R} \dif S'\\ &=\frac{\mu_0}{4\pi}\int_{V'} \frac{\bd{J}_m}{R}\dif V' + \frac{\mu_0}{4\pi}\int_{S'} \frac{\bd{J}_{sm}}{R} \dif V' \end{align} $$可以看出,媒质产生的磁场由内部与表面的束缚电流(磁化电流) $\bd{J}\_m$ 和 $\bd{J}_{sm}$ 组成,即:
$$ \bd{J}_m=\nabla\times \bd{M}(省略')\\ \bd{J}_{sm}=\bd{M}\times\bd{n} $$性质:
- 磁介质均匀且介质中无传导电流时,磁化体电流 $J_m=0$(想象内部电流环相互抵消)
- 磁介质表面总有磁化面电流 $J_{ms}\neq 0$
- 穿过整块介质的任意界面上的磁化电流总量等于0,$I_m+I_{sm}=0$(进去的电流等于出去的电流)
媒质中的安培环路定律
我们将媒质看作真空,设媒质中的等效磁化电流为 $I_m$,则:
$$ \oint_c \bd{B}\cdot\dif l=\mu_0 (I+I_m)\\ $$我们将 $I_m$ 写成:
$$ \begin{align} I_m&=\int_S J_m \cdot \dif \bd{S}\\ &=\int_S (\nabla\times\bd{M})\cdot \dif \bd{S}\\ &=\oint_c \bd{M} \cdot \dif l \end{align} $$将上式代入后:
$$ \oint_c \bd{B}\cdot \dif \bd{l} =\mu_0 (I+\oint_c \bd{M} \cdot \dif l)\\ \oint_c \left( \frac{\bd{B}}{\mu_0}-\bd{M} \right) \cdot \dif \bd{l}=I $$我们令 $\bd{H}=\frac{\bd{B}}{\mu_0}-\bd{M}$ 为 磁场强度,单位为 A/m。因为 $\bd{M}$ 与 $\bd{H}$ 成线性同向关系,即:
$$ \bd{M}=\chi_m \bd{H}\\ 磁化率:\chi_m $$所以我们可以得到 $\bd{B}$ 与 $\bd{H}$ 的本构关系:
$$ \begin{align} \bd{B}&=\mu_0(\bd{H}+\bd{M})\\ &=\mu_0(1+\chi_m) \bd{H}\\ &=\mu \bd{H} \end{align}\\ 磁导率:\mu $$所以我们得到媒质中的安培环路定理:
$$ 积分:\oint_C \bd{H}\cdot \dif \bd{l}=I\\ 微分:\nabla\times\bd{H}=\bd{J} $$