恒定电场
$$ \begin{align*} \newcommand{\dif}{\mathop{}\!\mathrm{d}}\\ \newcommand{\p}{\partial}\\ \newcommand{\bd}{\boldsymbol} \end{align*} $$电流
在电场中,导体回路中产生定向运动的电荷,称为 电流,用 电流强度(标量,简称电流)表示电流大小,其定义为 单位时间内通过某截面 S 的电荷量。
$$ I=\lim_{\Delta t\rightarrow0} \frac{\Delta q}{\Delta t}=\frac{\dif q}{\dif t} \quad (\rm{A}) $$体电流密度矢量
为了研究不同点的电荷运动情况,定义 电流密度矢量 $\bd{j}$:
$$ \bd{J}=\lim_{\Delta S\rightarrow} \frac{\Delta I}{\Delta S}\hat{n} = \frac{\dif I}{\dif S} \hat{n} \quad \mathrm{(A/m^2)}\\ I=\int_S \bd{J} \cdot \dif \bd{S} $$$\bd{n}$ 是正电荷运动的方向(电流方向),$\bd{S}$ 是在该点上垂直于 $\bd{n}$ 的面元。我们可以用 $\bd{J}$ 的矢量线来描绘电流场。
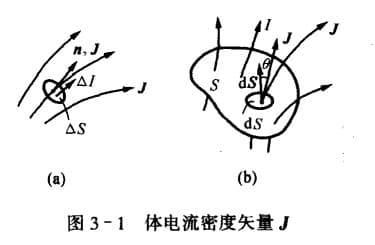
上面是电流密度的定义式,下面我们来求原理式。假设运动电荷的体密度 $\rho_v$ 和运动速度 $\bd{v}$:
$$ \dif q=\rho_v \bd{v} \dif t \dif S\\ \bd{J} = \frac{\dif \bd{I}}{\dif S}=\frac{\dif q/\dif t}{\dif S}=\rho_v \bd{v} $$对于多种带电电荷,有 $\bd{J} = \sum_i \rho_{Vi} \bd{v}_i$。注意,这里指的是运动电荷,与静电荷无关,所以净电荷为 0 时也能有电流。
面电流密度矢量
为了研究电流在厚度可忽略的薄层中流动的情况,我们引入 面电流密度矢量 $\bd{J}$:
$$ \bd{J}_S=\lim_{\Delta l \rightarrow 0} \frac{\Delta I}{\Delta l} \hat{n} \quad \mathrm{(A/m)}\\ \bd{I} = \int_l \bd{J}_S \cdot \bd{a}_\perp \dif l $$$\hat{n}$ 是电流方向,$\Delta l$ 是垂直于 $\hat{n}$ 的线元。也可以用面电荷密度 $\rho_{vs}$ 与速度 $\bd{v}$ 来表示:
$$ \bd{J}_S = \rho_{vs} \bd{v} $$线电流
线电流用密度与速度表示为:$I=\rho_{vl} v$
电流连续性方程
由电荷守恒,单位时间内,闭合曲面 $S$ 内的电荷减少量,等于从 $S$ 流出的电流,我们有:
$$ \int_S \bd{J} \cdot \dif \bd{S} = -\frac{\dif}{\dif t} \int_V \rho \dif V\\ \int_V \nabla \cdot \bd{J} \dif V = -\int_V \frac{\dif \rho}{\dif t} \dif V\\ \nabla \cdot \bd{J}=-\frac{\dif \rho}{\dif t} $$这是根据电荷守恒原理得出的,是电磁场中最基本的原理性方程。
恒定电场的基本方程
因为恒定电场中(电池外)的电场、电荷不随时间变化(电荷动态平衡),所以 $\frac{\dif \rho}{\dif t}=0$,从而:
$$ \nabla\cdot \bd{J}=0\\ \oint_S \bd{J}\cdot\dif\bd{S}=0 $$这说明电流是一个无散场,电流线是连续的,没有起点也没有终点。
同时,由于电流恒定,电荷分布不随时间改变,所以动态平衡下的分布电荷产生的库伦电场与静电场具有相同性质,即无旋:
$$ \nabla\times \bd{E}=0\\ \oint_c \bd{E}\cdot \dif \bd{l} = 0 $$欧姆定律
实验证明,对大部分导电媒质,有:
$$ \bd{J}=\sigma \bd{E} $$其中,$\sigma$ 称为导电媒质的电导率,由导体材料决定,单位是 S/m。我们称上式为 微分形式的欧姆定律
我们在长为 $l$,横截面为 $S$,的导体中对上式进行积分:
$$ \int_l \int_S \bd{J} \cdot \dif \bd{S} \dif l = \sigma \int_S \int_l \bd{E} \cdot \dif \bd{l} \dif S\\ I l = \sigma US\\ U = \frac{l}{\sigma S} I= RI $$就得到 积分形式的欧姆定律。
- 微分形式适用于任何连续导电媒质、任何传导电流;
- 积分形式指适用于均匀媒质、恒定电流;
如果自由电子在外电场的作用下离开导体产生传导电流1,导体中的正电荷会产生内电场,抵消外电场,导致传导电流消失,因此需要电源来维持电流。我们考虑电源内部,存在静电力,也存在非静电力(如化学作用),我们将非静电场定义为: $\bd{E}'$,则可以得到 含源的欧姆定律:
$$ \bd{J}=\sigma(\bd{E}+\bd{E}') $$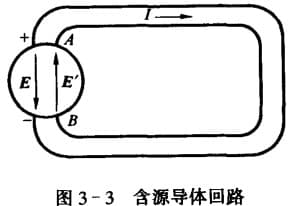
焦耳定律
运动的电子与晶体点阵上的电子碰撞,动能转化为热能,也就是电场力对电荷做得功最终转化为焦耳热。
我们考虑电场力对 $\dif V$ 中的元电荷 $\dif q = \rho_v \dif V$ 做的功:
$$ \dif A = \bd{F}\cdot \bd{l}= \bd{E}\cdot \bd{v} \dif q \dif t= \bd{E}\cdot \rho_v \bd{v} \dif V \dif t= \bd{E} \cdot \bd{J} \dif V \dif t $$从而功率为:
$$ p=\frac{\dif P}{\dif V}=\frac{\dif A / \dif t}{\dif V} = \bd{E} \cdot \bd{J} \quad \mathrm{(W/m^3)} $$上面的功都会转化为焦耳热。上式就是单位体积内的电流消耗功率,也就是 微分形式的焦耳定律。在线性各向同性的导电媒质中,$J=\sigma E$,所以:
$$ p = \bd{E} \cdot \bd{J}=\sigma \bd{E}^2 $$对上式积分就能得到 积分形式的焦耳定律:
$$ P = \int_V p \dif V = \int_l \bd{E} \cdot \dif \bd{l} \int_S \bd{J} \cdot \dif \bd{S} =UI $$分界面上的边界条件
当电流通过不同电导率的两种媒质的分界面时,$\bd{J}$ 和 $\bd{E}$ 都会发生变化。
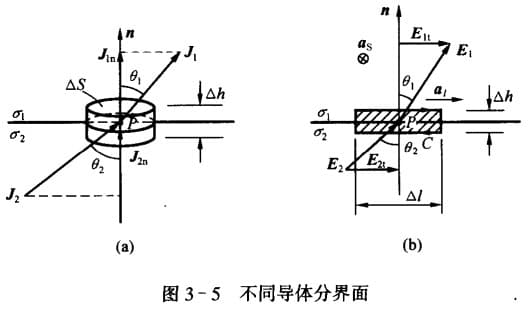
对上图(a)所示的圆柱面,有:
$$ \oint_S \bd{J}\cdot\dif \bd{S}=\bd{J}_1\cdot \bd{n}\Delta S - \bd{J}_2 \cdot \bd{n} \Delta S=0\\ \therefore \bd{n}\cdot \bd{J}_1 = \bd{n} \cdot \bd{J}_2 \quad \mathrm{or} \quad J_{1n}=J_{2n} $$说明分界面上电流密度矢量对界面的法向分量是连续的。
对上图(b)所示的矩形,有:
$$ \oint_c \bd{E}\cdot \dif \bd{l} = \bd{E}_1\cdot\bd{a}_l\Delta l-\bd{E}_1\cdot\bd{a}_l \Delta l=0\\ \therefore \bd{n}\times\bd{E}_1=\bd{n}\times\bd{E}_2 \quad\mathrm{or}\quad E_{1t}=E_{2t} $$根据上面两个分界条件,我们有:
$$ \begin{cases} J_{1n}=J_{2n}\\ E_{1t}=E_{2t} \end{cases}\\ 或 \begin{cases} \sigma_1 \frac{\p \phi_1}{\p n}=\sigma_2 \frac{\p \phi_2}{\p n}\\ \phi_1=\phi_2 \end{cases} $$上两式相除,我们有:
$$ \frac{\tan\theta_1}{\tan\theta_2}=\frac{\sigma_1}{\sigma_2} $$电导与接地电阻
两导体间的媒质的电导定义为:$G=\dfrac{I}{U}$,电导只与电极结构(形状、尺寸、位置)和媒质有关,与电荷无关。
电导的计算:
- 用电流计算
- $假设 I\rightarrow \vec{E}=\frac{\vec{J}}{\sigma}\rightarrow $$U=\int \vec{E}\cdot\dif \vec{l}\rightarrow G=\frac{I}{U}$
- $假设 U\rightarrow \vec{J}=\sigma \vec{E}\rightarrow $$I=\int \vec{J}\cdot\dif \vec{S}\rightarrow G=\frac{I}{U}$
- 静电比拟法
- $\dfrac{C}{G}=\dfrac{Q/U}{I/U}=\dfrac{Q}{I}=$$\dfrac{\oint_s \vec{D}\cdot\dif\vec{S}}{\oint_s \vec{J}\cdot\dif\vec{S}}=\dfrac{\varepsilon}{\sigma}$
对于接地的设备,我们将电流经过接地体流入大地时的电阻统称为 接地电阻,包括导线电阻、接地体电阻、接地体与大地的解出电阻、电流在土壤中的电阻。在接地体附近,由于地面存在接地电流,如果人走在上面,会有 跨步电压。
静电场与恒定电场比较

可见,只要求出一个场,就能对应得出另一个场的对应量。
传导电流:传导电流中的带电微粒(如金属中的自由电子、电解质溶液中的正负离子、气体中的离子和电子)在电场作用下,在导体内部做定向运动而形成的电流。(百度百科) ↩︎