泊松方程与边界条件

$$ \begin{align*} \newcommand{\dif}{\mathop{}\!\mathrm{d}}\\ \newcommand{\p}{\partial}\\ \newcommand{\bd}{\boldsymbol} \end{align*} $$

泊松方程

高斯定理给出了电场（电位移矢量）与电荷的关系，而泊松方程则给出了电位与电荷的关系：

$$ \begin{cases} \nabla \cdot \vec{D} =\rho\\ \vec{D}=\varepsilon\vec{E}\\ \vec{E}=-\nabla \phi \end{cases} \Longrightarrow \nabla^2 \phi=-\frac{\rho}{\varepsilon} $$

上式即 泊松方程。特殊地，当电荷密度为 0 时，$\nabla^2 \phi=0$ 称为 拉普拉斯方程，$\nabla^2 = \frac{\p}{\p x^2}+\frac{\p}{\p y^2}+\frac{\p}{\p z^2}$ 称为拉普拉斯算子。对于不同坐标系，拉普拉斯算子分别为：

直角坐标{:.success}

$$ \nabla^2 \phi= \frac{\p \phi}{\p x^2}+\frac{\p \phi}{\p y^2}+\frac{\p \phi}{\p z^2} $$

柱坐标{:.success}

$$ \nabla^2 \phi=\frac{1}{r}\frac{\p}{\p r}\left(r \frac{\p \phi}{\p r} \right)+\frac{1}{r^2}\frac{\p^2 \phi}{\p \varphi^2}+\frac{\p \phi}{\p z^2} $$

球坐标{:.success}

$$ \nabla^2 \phi= \frac{1}{r^2}\frac{\p}{\p r}\left(r \frac{\p \phi}{\p r} \right)+\frac{1}{r^2\sin\theta}\frac{\p}{\p \theta}\left(\sin\theta\frac{\p \phi}{\p \theta}\right)+\frac{1}{r^2\sin^2\theta}\frac{\p^2 \phi}{\p \varphi^2} $$

利用 Lame 系数，可以写成：

$$ \nabla^2 = \frac{1}{h_1h_2h_3} \sum_{i=1}^3 \frac{\p}{\p u_i} \left( \frac{h_1h_2h_3}{h_i} \frac{\p}{h_i \p u_i} \right) $$

有时候 $\nabla^2$ 也会用于矢量，表示对分量分别求梯度的散度：

$$ \nabla^2 \vec{E} = (\nabla^2 E_1) \hat{a}_1+(\nabla^2 E_2) \hat{a}_2+(\nabla^2 E_3) \hat{a}_3 $$

拉普拉斯算子具有与梯度与散度类似的性质：

• 分配律：$\nabla^2(u+v)=\nabla^2 u + \nabla^2 v$
• $\nabla^2(uv)=u\nabla^2 v+2\nabla u \cdot \nabla v +v\nabla^2 u$
• $\nabla \times (\nabla\times \vec{F}) = \nabla(\nabla\cdot\vec{F}) - \nabla^2\vec{F}$

边界条件

需要对 $\nabla^2 \phi$ 进行两次积分才能求得 $\phi$，这样会产生两个常数 $C_1, C_2$，因此需要两个边界条件。我们通过下面例题来体会：

答案

Note

解： 以球心为坐标原点建立球坐标系。在 $a\lt r\lt \infty$ 处，电位函数满足拉普拉斯方程，并且在球外电荷密度为 0，所以：

$$ \nabla^2\phi = \frac{1}{r^2}\frac{\p}{\p r}\left(r \frac{\p \phi}{\p r} \right)=0\\ \phi=-\frac{C_1}{r}+C_2 $$

由边界条件：

$$ \begin{cases} \phi(a)=U\\ \phi(\infty)=0 \end{cases} \Rightarrow \begin{cases} C_2=0\\ C_1=-aU \end{cases} $$

最终解出：

$$ \phi(r)=\frac{aU}{r} \; (a

分界面上的边界条件

进行 $\nabla^2 \phi$ 或 $\nabla\cdot \vec{D}$ 运算的前提是“可微”，若在介质分界面上，则无法进行微分，此时只能用积分形式，而此时的边界条件只能用积分来推导。下面就介绍推导过程。

电位移的边界条件

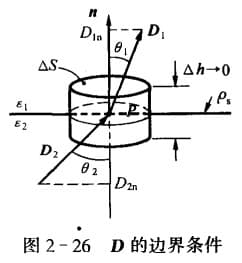
如图所示，$\vec{D}_1$ 和 $\vec{D}_2$ 对应于介质 $\varepsilon_1$ 和 $\varepsilon_2$ 的电位移矢量。我们取一无穷小的圆柱体，根据对称性，侧面上的通量为0，由高斯通量定理：

$$ \oint_S \vec{D}\cdot\dif \vec{S}=\vec{D}_1\cdot\vec{n}\Delta S - \vec{D}_2\cdot\vec{n}\Delta S=\rho_s\Delta S\\ 即：\vec{n}\cdot(D_1 - D_2)=\rho_s\\ 或：D_{1n}-D_{2n}=\rho_s $$

说明垂直于分界面上的电位移通量分量之差，等于界面上的自由电荷面密度。若分界面上无自由电荷，则：

$$ \vec{n}\cdot\vec{D}_1=\vec{n}\cdot\vec{D}_2\\ D_{1n}=D_{2n} $$

此时电位移通量在分界面上连续。

进一步，由电位移矢量与电场、电位的关系：

$$ D_n=\varepsilon E_n=\varepsilon \vec{E}\cdot\vec{n}=\varepsilon(-\nabla\phi)\cdot\vec{n}=-\varepsilon\frac{\p \phi}{\p \vec{n}} $$

从而有：

$$ \varepsilon_1 E_{n1}-\varepsilon_2 E_{n2}=\rho_s\\ -\varepsilon_1\frac{\p \phi_1}{\p \vec{n}}+\varepsilon_2\frac{\p \phi_2}{\p \vec{n}}=\rho_2 $$

电场强度的边界条件

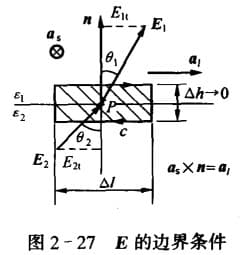
我们取一极小的闭合矩形路径，对 $E_1$ 和 $E_2$ 做线积分，由于左右的对称形，故积分为 0，从而由闭合路径电场积分为 0：

$$ \oint_c \vec{E} \cdot \dif \vec{l}=\vec{E}_1 \cdot \vec{a}_l \Delta l - \vec{E}_2\cdot \vec{a}_l \Delta l =0 $$

我们 $\vec{a}_s$ 是垂直纸面向里的向量，即：$\vec{a}_l=\vec{a}_s\times \vec{n}$，同时由矢量恒等式：

$$ \bd{A}\cdot(\bd{B}\times\bd{C})=\bd{B}\cdot(\bd{C}\times\bd{A})\\ \vec{E}\cdot(\vec{a}_s\times \vec{n})=\vec{a}_s\cdot(\vec{n}\times \vec{E}) $$

从而：

$$ \vec{n}\times \vec{E}_1-\vec{n}\times \vec{E}_2=0\\ E_{1t}=E_1\cos\theta_1=E_2\cos\theta_2=E_{2t} $$

上式说明，电场强度对于界面的切向分量在界面上是连续的，从而分界面上的电位 $\phi=\int E$ 也是连续的。注意的是，这里的连续是切线方向上的连续，上面说的是法线方向上不连续。

理想介质分界面

在两种理想介质分界面上没有自由电荷，即 $\rho_s=0$，则有：

$$ \begin{cases} \vec{n}\times \vec{E}_1=\vec{n}\times \vec{E}_2\\ \varepsilon_1 \vec{E}_1\cdot\vec{n}=\varepsilon_2 \vec{E}_2\cdot\vec{n} \end{cases}\\ 即 \begin{cases} E_1\sin\theta_1=E_2\sin\theta_2\\ \varepsilon_1 E_1\cos\theta_1=\varepsilon_2E_2\cos\theta_2 \end{cases} $$

将上两式相除得到：

$$ \frac{\tan\theta_1}{\tan\theta_2}=\frac{\varepsilon_2}{\varepsilon_1} $$

上式称为静电场的折射定理，即 $\vec{D}$ 和 $\vec{E}$ 矢量在两种介质分界面上要改变方向，除非 $\theta_1=\theta_2=0$（比如平行板、同轴线、同心球中的电场）。

更多

• Boundary Conditions on E,H,D,B