Z变换分析

$$ \begin{align*} \newcommand{\dif}{\mathop{}\!\mathrm{d}} \newcommand{\belowarrow}[1]{\mathop{#1}\limits_{\uparrow}} \newcommand{\bd}{\boldsymbol} \newcommand{\L}{\mathscr{L}} \newcommand{\xleftrightarrow}[1]{\stackrel{#1}{\longleftrightarrow}} \end{align*} $$

复习

在信号与系统中已经讲过 z 变换了，请回去复习一下：

• 信号与系统 - z变换
• 信号与系统 - z变换分析

当然，我这里还是快速过一次吧。z变换的定义如下：

$$ X(z) = \sum_{n=-\infty}^{\infty} x[n] z^{-n} $$

由级数理论，级数收敛的充分必要条件为绝对可和，即：

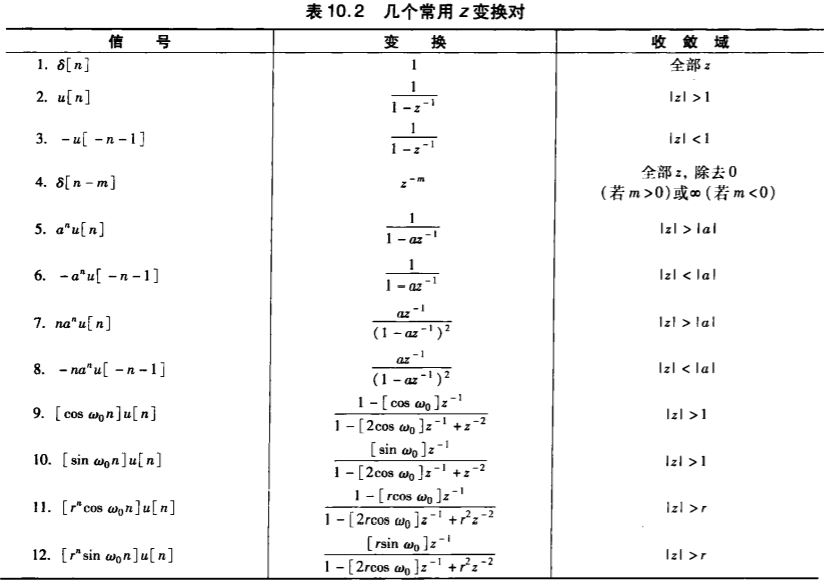
$$ \sum_{n=-\infty}^{\infty} |x[n]z^{-n}|=\sum_{n=-\infty}^{\infty} |x[n]r^{-n}e^{-j\omega n}|\leq \sum_{n=-\infty}^{\infty} |x[n]r^{-n}|<\infty $$

可见收敛域（ROC）与 $r$ 的取值有关，所以 ROC 是圆环形的。当我们计算 z 变换时，要求出其收敛域。P.S.，常见 z 变换如下：

求解逆 z 变换有 3 种方法：

• 部分分式展开法
• 幂级数展开法（长除法）
• 围线积分

这些东西请看回信号与系统，我懒得再写一遍了。

传输函数

LTI系统的输入输出关系满足：

$$ y[n]=\sum_{k=-\infty}^{+\infty} h[k]x[n-k]\\ \xleftrightarrow{z} Y(z)=H(z)X(z) $$

$H(z)$ 称为 传递函数 或 系统函数。

LTI系统一般用差分方程描述：

$$ \sum_{k=0}^{N} d_k y[n-k]=\sum_{k=0}^{M} p_k x[n-k]\\ \text{本课程只考虑 }d_k,p_k \text{ 是实数的情况} $$

对两边做z变换，移项，可以得到传递函数为：

$$ H(z)=\frac{Y(z)}{X(z)}=\frac{\sum_{k=0}^M p_k z^{-k}}{\sum_{k=0}^N d_k z^{-k}}=\frac{p_0\prod_{l=1}^M (z-\xi_l)}{d_0\prod_{l=1}^M (z-\lambda_l)} $$

对于 FIR 系统，由于 $N=0$（也就是只有 $y[n]$ 项，没有 $y[n-k]$ 项），所以其传递函数的形式为：$H(z)=\sum_{n=M_1}^{M_2} h[n] z^{-n}$，$0\leq M_1 \leq M_2$，极点在 $z=0$ 处，所以收敛域为除 $z=0$ 外的整个 z 平面。

对于 IIR 系统，由于是因果系统，所以收敛域为 $\vert z\vert > \max_k \vert \lambda_k \vert$，$\lambda_k$ 为极点。

习题

$$ \begin{aligned} x_1[n]&=\alpha^n u[n+1] + \beta^n u[n+2]\\ x_2[n]&=\alpha^n u[n-2] + \beta^n u[-n-1]\\ x_3[n]&=\alpha^n u[n+1] + \beta^n u[-n-1] \end{aligned} $$

[!NOTE] 解：通过已学知识可知：
    常用z变换对 $u[n] \xleftrightarrow{z} \frac{1}{1-z^{-1}}, \vert z \vert>1$
    时移：$x[n-m] \xleftrightarrow{z} z^{-m}X[z]$，影响 0 和 $\infty$ 的收敛性
    时反：$x[-n] \xleftrightarrow{z} X[z^{-1}]$，收敛域为原收敛域的点的倒数集合
    指数加权：$a^n x[n] = \xleftrightarrow{z} X[a^{-1}z]$，收敛域拉伸为 $\vert a \vert$ 倍
  因此，可以直接写出 z 变换：

$$ \begin{aligned} X_1(z)&=\frac{1}{\alpha z^{-1}}\cdot\frac{1}{1-\alpha z^{-1}} + \frac{1}{\beta^2 z^{-2}}\cdot\frac{1}{1-\beta z^{-1}}, |\beta|<|z|<\infty\\ X_2(z)&=\frac{\alpha^2 z^{-2}}{1-\alpha z^{-1}}-\frac{\beta z^{-1}}{1-\beta^2 z^{-1}}, |\alpha|<|z|<|\beta|\\ X_3(z)&=\frac{1}{\alpha^2 z^{-2}}\cdot\frac{1}{1-\alpha z^{-1}}-\frac{\beta z^{-1}}{1-\beta^2 z^{-1}}, |\alpha|<|z|<|\beta| \end{aligned} $$

[!NOTE] 解：极点为：$\lambda_1 = -0.6$，$\lambda_2=\lambda_3=0.4$，所以可能的收敛域为：

$$ \begin{aligned} &\text{ROC}_1: |z|<0.4\\ &\text{ROC}_2: |0.4|<|z|<0.6\\ &\text{ROC}_3: |z|>0.6 \end{aligned} $$

$$ X_c(z) = \frac{2}{1+0.6z^{-1}}+\frac{3}{1-0.4z^{-1}}+\frac{-1}{(1-0.4z^{-1})^2} $$

• $\text{ROC}_2$：$x_1[n] = -2(-0.6)^n u[-n-1] - 3 (0.4)^n u[-n-1]+2.5(n+1)(0.4)^{(n+1)} u[-n-2]$
• $\text{ROC}_3$：$x_2[n] = -2(-0.6)^n u[-n-1] + 3 (0.4)^n u[n]-2.5(n+1)(0.4)^{(n+1)} u[n+1]$
• $\text{ROC}_4$：$x_2[n] = 2(-0.6)^n u[n] + 3 (0.4)^n u[n]-2.5(n+1)(0.4)^{(n+1)} u[n+1]$

[!CAUTION]

[!TIP] 6.38 利用多项式相乘法计算： $g[n]=\{-3, 2,5\}$ 和 $h[n]=\{4,-3,1,-4\}$ 的线性卷积和圆周卷积

[!NOTE] 解：先写出传递函数：

$$ \begin{aligned} G(z)&=-3+2z^{-1}+5z^{-2}\\ H(z)&=4-3z^{-1}+z^{-2}-5z^{-3} \end{aligned} $$

则线性卷积为：

$$ \begin{aligned} Y_L(z)&=G(z)H(z)\\ &=-12+17z^{-1}+11z^{-2}-z^{-3}-3z^{-4}-20z^{-5} \end{aligned} $$

圆周卷积为：

$$ \begin{aligned} Y_C(z)&=\langle Y_L(z) \rangle_{(z^{-4}-1)}\\ &=-12+17z^{-1}+11z^{-2}-z^{-3}-3-20z^{-1}\\ &=-15-3z^{-1}+11z^{-2}-z^{-3} \end{aligned} $$

当 $\omega = \frac{2k \pi}{R}$ 时取最大值 $1+\vert \alpha \vert$；当 $\omega = \frac{(2k+1) \pi}{R}$ 时取最小值 $1-\vert \alpha \vert$。

[!TIP] 6.81 LTI离散时间系统的传输函数为：

$$ H(z)=\frac{3(z+1.8)(z-4)}{(z+0.3)(z-0.6)(z+5)} $$

问：该系统的频率响应 $H(e^{j\omega})$ 是否存在？该系统可能稳定吗？可能是因果的吗？并在不求逆 z 变换的情况下确定 $h[n]$ 的形式。