DCT变换
$$ \begin{align*} \newcommand{\dif}{\mathop{}\!\mathrm{d}} \newcommand{\belowarrow}[1]{\mathop{#1}\limits_{\uparrow}} \newcommand{\bd}{\boldsymbol} \newcommand{\L}{\mathscr{L}} \newcommand{\xleftrightarrow}[1]{\stackrel{#1}{\longleftrightarrow}} \end{align*} $$老师要求在课堂上讲一种变换,感觉 DCT 还是挺有趣的,就决定讲它了!
DCT(简单易懂版)
DCT,Discrete Cosine Transfrom,离散余弦变换,主要用于图像压缩中,比如 jpeg。
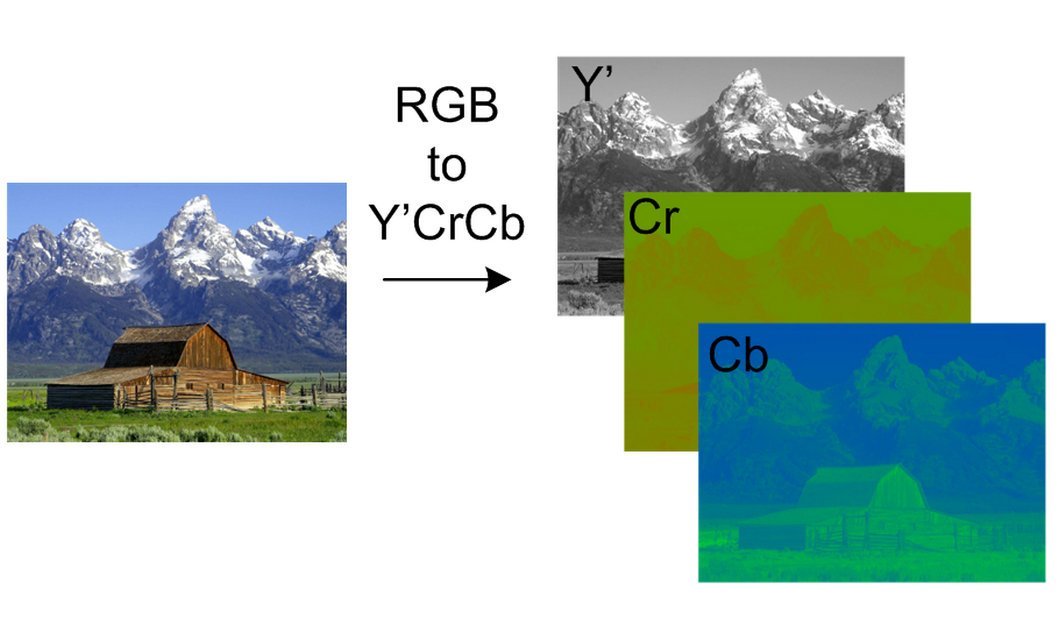
一般来说,我们人眼对灰度没那么敏感,对颜色比较敏感。所以我们一般不用三原色(RGB)来表示图片,而是用 YCrCb,如下图所示:
然后我们对灰度图进行压缩。根据前面的内容,我们知道可以用不同频率的余弦函数的线性组合来表示任意函数,在图片中也是一样,对于任意的 8x8 灰度图,我们都可以用下面一系列离散余弦函数来表示:

我们取灰度图中的一个 8x8 矩阵的为例,数值越大,颜色越浅:
$$ \begin{array}{|c|c|c|c|c|c|c|c|} \hline 62 & 55 & 55 & 54 & 49 & 48 & 47 & 55\\ \hline 62 & 57 & 54 & 52 & 48 & 47 & 48 & 53\\ \hline 61 & 60 & 52 & 49 & 48 & 47 & 49 & 54\\ \hline 63 & 61 & 60 & 60 & 63 & 65 & 68 & 65\\ \hline 67 & 67 & 70 & 74 & 79 & 85 & 91 & 92\\ \hline 82 & 95 & 101 & 106 & 114 & 115 & 112 & 117\\ \hline 96 & 111 & 115 & 119 & 128 & 128 & 130 & 127\\ \hline 109 & 121 & 127 & 133 & 139 & 141 & 140 & 133\\ \hline \end{array} $$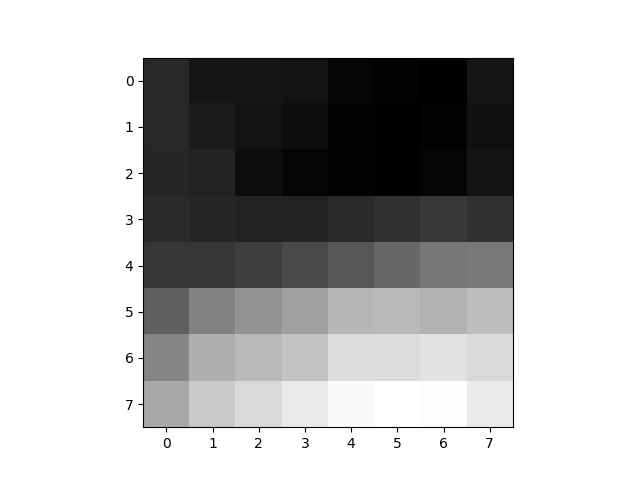
然后我们对这个进行归一化,归一到 -128~127(因为cos的值在 -1~1 之间),也就是每个值减去 128
$$ \begin{array}{|c|c|c|c|c|c|c|c|} \hline -66&-73&-73&-74&-79&-80&-81&-73\\ \hline -66&-71&-74&-76&-80&-81&-80&-75\\ \hline -67&-68&-76&-79&-80&-81&-79&-74\\ \hline -65&-67&-68&-68&-65&-63&-60&-63\\ \hline -61&-61&-58&-54&-49&-43&-37&-36\\ \hline -46&-33&-27&-22&-14&-13&-16&-11\\ \hline -32&-17&-13&-9&0&0&2&-1\\ \hline -19&-7&-1& 5 & 11 & 13 & 12 & 5\\ \hline \end{array} $$然后进行 DCT 变换,也就是计算每个余弦函数的系数,得到:
$$ \begin{array}{|c|c|c|c|c|c|c|c|} \hline -211.8 & 9.2 & 6.3 & -2.7 & 5.3 & 0.8 & 3.1 & -1.1\\ \hline -213.2 & 10.5 & 7.7 & -1.7 & 3.2 & 0.4 & 1. & -0.7\\ \hline -213.5 & 9.5 & 10.2 & -0.9 & 1.4 & -2.5 & -1.2 & -0.8\\ \hline -183.5 & -5.6 & 3.1 & 3.1 & -1.1 & 1.1 & -0.9 & 1.1\\ \hline -141.1 & -26.9 & 3.3 & 0.7 & -0.4 & 1.3 & -0.2 & 0.4\\ \hline -64.3 &-28.9 & -11.4 & -3.8 & -1.4 & -6.1 & 0.1 & -0.6\\ \hline -24.7 & -27.6 & -11.5 & -2.2 & -4.9 & -4.3 & -3.7 & 1.3\\ \hline 6.7 & -24.1 & -15.2 & 0.4 & -5.3 & -1.2 & -2.5 & 0.1\\ \hline \end{array} $$这里我们为了方便看,仅保留一位小数。注意到这个矩阵有个特点:左上角的数字比较大,右下角的数字比较小。这是因为图片中的低频分量大,高频分量比较小(PS. 人眼对高频分量不敏感,高频就是压缩中损失的部分)。
注意此时还未进行压缩(不考虑舍去小数点),我们依然可以进行 IDCT 变换得到原图。那么如何压缩呢?我们先定义一个量化表(difine quantization table),如下左:
$$ \begin{array}{|c|c|c|c|c|c|c|c|} \hline 6 & 12&14&14&18&24&49&72\\ \hline 11&12&13&17&22&35&64&92\\ \hline 10&14&16&22&37&55&78&95\\ \hline 16&19&24&29&56&64&87&98\\ \hline 24&26&40&51&68&81&103&112\\ \hline 40&58&57&87&109&104&121&100\\ \hline 48&60&69&80&103&113&120&103\\ \hline 51&55&56&62&77&92&101&99\\ \hline \end{array}\quad \begin{array}{|c|c|c|c|c|c|c|c|} \hline -35 & 1&0 & 0&0&0& 0 & 0 \\ \hline -19&1&1 & 0&0&0& 0&0 \\ \hline -21&1&1 & 0& 0&0&0&0 \\ \hline -12 & 0&0&0 & 0& 0&0& 0 \\ \hline -6 & -1& 0&0&0& 0&0& 0 \\ \hline -2 & 0 & 0 & 0&0&0&0&0 \\ \hline 0 & 0 & 0 & 0&0&0&0& 0 \\ \hline 0 & 0 & 0&0&0 & 0&0& 0 \\ \hline \end{array} $$然后将DCT变换后得到的矩阵中的每个数字,除以量化表对应的数,再取最近的整数,得到上面右边的矩阵。可以很明显的看出,最终只有左上角的数不为0,其余大部分数都为0。这说明量化表的数字越大,压缩率越高。然后我们以 Z字形的顺序,从左上到右下将这个矩阵保存为一个数组,再利用霍夫曼编码,就可以实现图片的压缩,得到 JPEG 图像。
反编码很简单。乘以表格,然后再进行 IDCT 变换即可。最终得到图片如下:
| 原图 | 压缩图 |
|---|---|
 | 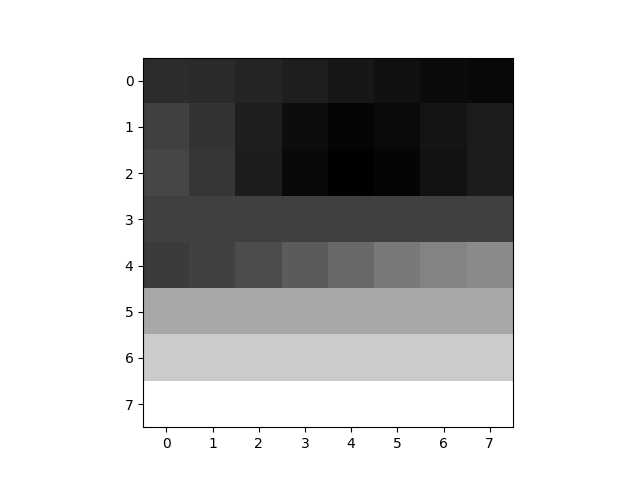 |
放大了看可以很明显的看出差异,但注意这只是一张图片中的 8x8 个像素,放在图片中我们是分辨不出差异的。
总结一下得到 JPEG 的过程:
- RGB 转 YCrCb
- DCT
- 量化
- 霍夫曼编码
- JPEG!
JPEG 图片中会存储量化表,每个图片的量化表是不同的。
#DCT实验 #Python
import matplotlib.pyplot as plt
import numpy as np
from scipy.fft import dct, idct
np.set_printoptions(precision=1, suppress=True)
origin_pic = np.array(
[
[62, 55, 55, 54, 49, 48, 47, 55],
[62, 57, 54, 52, 48, 47, 48, 53],
[61, 60, 52, 49, 48, 47, 49, 54],
[63, 61, 60, 60, 63, 65, 68, 65],
[67, 67, 70, 74, 79, 85, 91, 92],
[82, 95, 101, 106, 114, 115, 112, 117],
[96, 111, 115, 119, 128, 128, 130, 127],
[109, 121, 127, 133, 139, 141, 140, 133],
]
)
plt.figure("origin picture")
plt.imshow(origin_pic, cmap="gray")
plt.show()
centered_pic = origin_pic - 128
dct_pic = dct(centered_pic, 2, norm="ortho")
table = np.array(
[
[6, 12, 14, 14, 18, 24, 49, 72],
[11, 12, 13, 17, 22, 35, 64, 92],
[10, 14, 16, 22, 37, 55, 78, 95],
[16, 19, 24, 29, 56, 64, 87, 98],
[24, 26, 40, 51, 68, 81, 103, 112],
[40, 58, 57, 87, 109, 104, 121, 100],
[48, 60, 69, 80, 103, 113, 120, 103],
[51, 55, 56, 62, 77, 92, 101, 99],
]
)
compressed_pic = np.around(dct_pic / table)
print(compressed_pic)
decode_pic = idct(compressed_pic * table, 2, norm="ortho") + 128
plt.figure("compressed picture")
plt.imshow(decode_pic, cmap="gray")
plt.show()