系列
数字信号处理
5-有限长离散时间变换
离散傅里叶变换实验

离散傅里叶变换实验

$$ \begin{align*} \newcommand{\dif}{\mathop{}\!\mathrm{d}} \newcommand{\belowarrow}[1]{\mathop{#1}\limits_{\uparrow}} \newcommand{\bd}{\boldsymbol} \newcommand{\L}{\mathscr{L}} \newcommand{\xleftrightarrow}[1]{\stackrel{#1}{\longleftrightarrow}} \end{align*} $$

实验要求

  1. 验证性实验
    • 用 Matlab 验证DFT运算的对称性质
    • 编程计算出一个2N点的实序列的频谱，要求只使用一次 N 点的 FFT 和其他运算，并与一次 2N 点 FFT 作出的频谱进行比较验证
  2. 应用性实验
    • 去中国期刊网、IEEE网站等查找频率估计方法，利用至少两种频率估计方法编程求给定信号的频率 ，要求：
      • 所有算法使用相同点数的FFT（小于等于100点）
      • 无噪声、20dB、10dB、5dB、0dB、-5dB，每个信噪比至少100次（无噪声除外）
      • 绘出估计均方误差图
      • 信号来源：用采样率8000Hz，对频率为350Hz的单频正弦信号进行采样，取70个点作为原始信号（无噪声）
    • 线性调频信号LFM： $x(nT)=\exp(j2\pi f_0 nT+j \pi u (nT)^2)$，$f_0$ 为中心频率，$T$ 为信号采样间隔，$u$ 为调频率，要求：
      • 在LFM信号中加入噪声信号 $n(t)$,采用匹配滤波器的方法对LFM信号进行脉冲压缩，并观察效果。$h(t)=s^*(t_0-t)$
      • 查阅文献，不同类型的失配滤波器，并用其对LFM信号进行脉冲压缩，并观察效果。

实验过程

验证DFT的对称性质

DFT 的对称性质包括：

序列DFT
$x[n]=x_\text{re}[n]+j x_\text{im}[n]$$X[k]=X_\text{re}[k]+j X_\text{im}[k]$
$x^*[n]$$X^*[\langle-k\rangle_N]$
$x^*[\langle-n\rangle_N]$$X^*[k]$
$x_\text{re}[n]$$X_\text{cs} =\frac{1}{2} \{ X[k]+X^*[\langle -k \rangle_N] \}$
$j x_\text{im}[n]$$X_\text{ca}[k]=\frac{1}{2} \{ X[k]-X^*[\langle -k \rangle_N] \}$
$x_\text{cs}[n]$$X_\text{re}[k]$
$x_\text{ca}[n]$$jX_\text{im}[k]$

由共轭对称性可以推导出后面四条式子，所以我们只验证后面两条式子。我们使用的 $x[n]$ 为：

$$ \begin{bmatrix} 4j & 1+3j & 2+2j & 3+j & 4 \end{bmatrix} $$

为了方便作图，我们定义 dftplot.m 如下：

function dftplot(xn)
%plot xn and Xk
    N = length(xn);
    n = 0:(N-1);
    Xk = fft(xn);

    subplot(321);
    stem(n, real(xn));
    title('real of x_n');
    xlabel('n');

    subplot(322);
    stem(n,imag(xn));
    title('image of x_n');
    xlabel('n');

    subplot(323);
    stem(n, abs(Xk));
    title('abs of X_k');
    xlabel('k');

    subplot(324);
    stem(n, angle(Xk));
    title('angle of X_k');
    xlabel('k');

    subplot(325);
    stem(n, real(Xk));
    title('real of X_k');
    xlabel('k');

    subplot(326);
    stem(n, imag(Xk));
    title('image of X_k');
    xlabel('k');
end

然后我们求 $x_\text{cs}$ 和 $x_\text{ca}$，我们定义 csca.m 如下：

function [x_cs,x_ca] = csca(x)
%computes x_cs and x_ca of x
    N = length(x);
    n = [0:N-1];
    xc = conj(x(mod(-n, N)+1));
    x_cs = 0.5*(x + xc);
    x_ca = 0.5*(x - xc);
end

利用这个求出 $x_\text{cs}$ 和 $x_\text{ca}$，并作出图像：

x = [4j 1+3j 2+2j 3+j 4];
[x_cs,x_ca] = csca(x);
dftplot(x);
figure;
dftplot(x_cs);
figure;
dftplot(x_ca);
$x[n]$$x_\text{cs}[n]$$x_\text{ca}[n]$
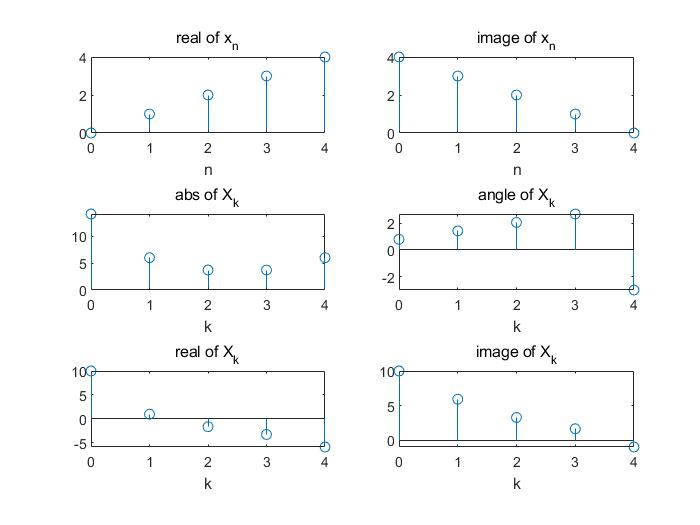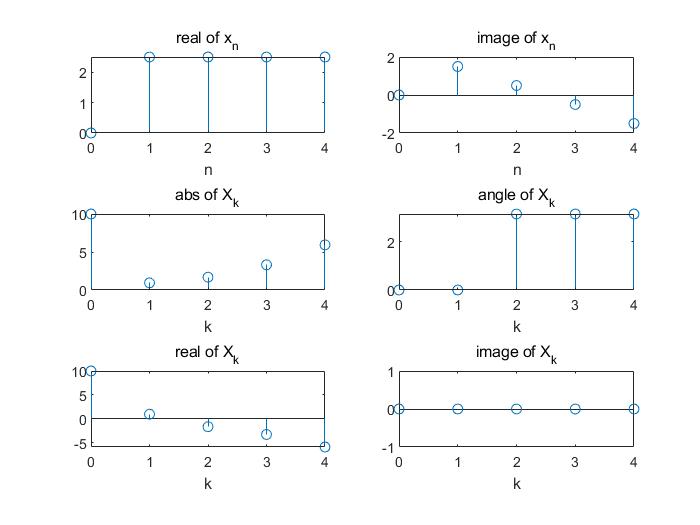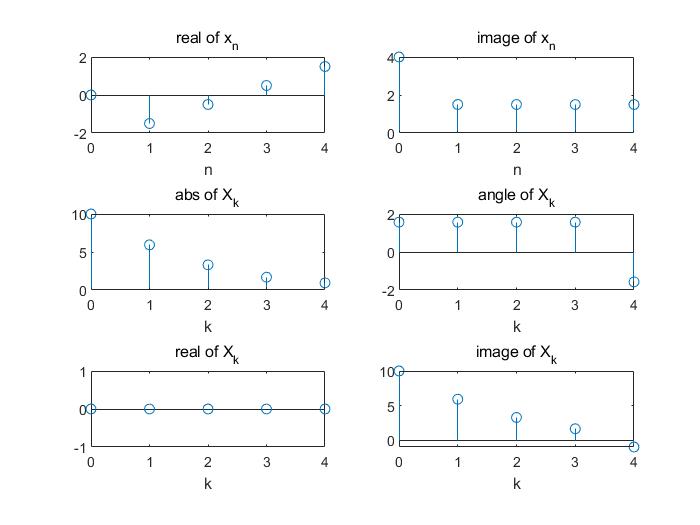dsp_exp2_111dsp_exp2_112dsp_exp2_113

观察最后一行可以发现，$x_\text{cs}[n]$ 的 DFT 为 $X_\text{re}[k]$，$x_\text{ca}[n]$ 的 DFT 为 $X_\text{im}[k]$。

仿照上面的过程，可以证明 $x_\text{re}[n]$ 的 DFT 为 $X_\text{cs}[k]$，$x_\text{im}[n]$ 的 DFT 为 $X_\text{ca}[k]$。先定义 idftplot.m，方便后面作图：

subplot(321);
    stem(n, real(xn));
    title('real of x_n');
    xlabel('n');

    subplot(322);
    stem(n,imag(xn));
    title('image of x_n');
    xlabel('n');

    subplot(323);
    stem(n, abs(Xk));
    title('abs of X_k');
    xlabel('k');

    subplot(324);
    stem(n, angle(Xk));
    title('angle of X_k');
    xlabel('k');

    subplot(325);
    stem(n, real(Xk));
    title('real of X_k');
    xlabel('k');

    subplot(326);
    stem(n, imag(Xk));
    title('image of X_k');
    xlabel('k');

然后求出 $X_\text{cs}$ 和 $X_\text{ca}$，并作出图像：

X = fft(x);
[X_cs, X_ca] = csca(X);
idftplot(X)
figure;
idftplot(X_cs);
figure;
idftplot(X_ca);
$X[k]$$X_\text{cs}[k]$$X_\text{ca}[k]$
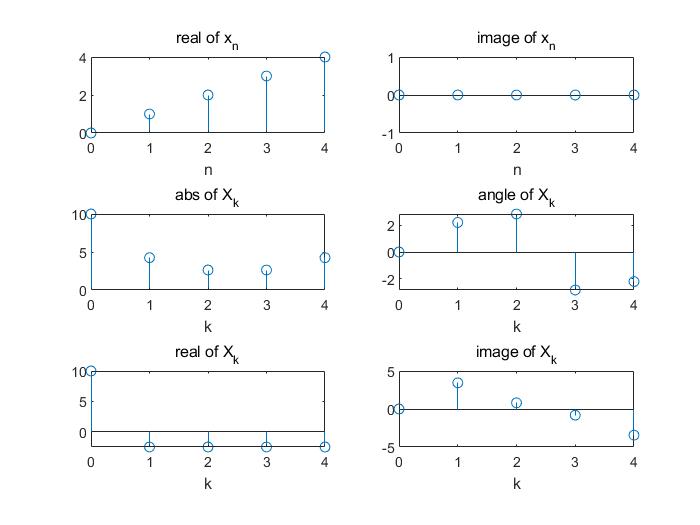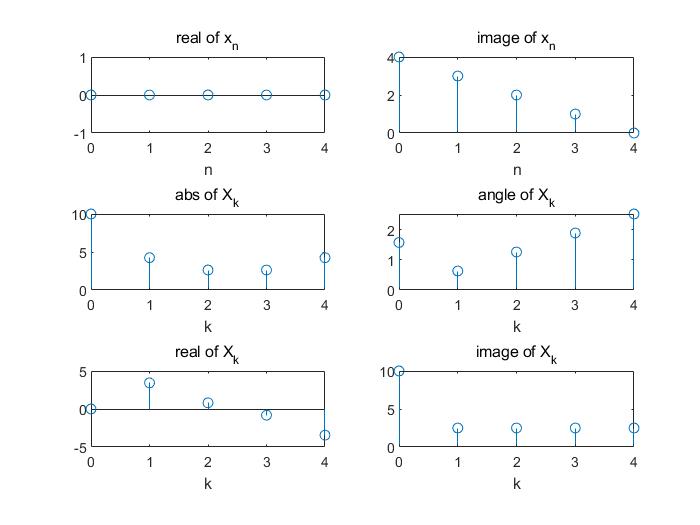dsp_exp2_111dsp_exp2_115dsp_exp2_116

注意第一行，$x_\text{re}[n]$ 的 DFT 为 $X_\text{cs}[k]$，$x_\text{im}[n]$ 的 DFT 为 $X_\text{ca}[k]$。

综上，可以验证 DFT 的对称性质成立。

利用n点DFT求2n点实序列DFT

求解过程如下：

function Xk = nfft(xn)
    N = length(xn);
    n = 0:(N-1);

    if mod(N,2) ~= 0
        error('the length of xn must be 2n')
    end

    gn = xn(2:2:N); %偶数
    hn = xn(1:2:N); %奇数

    yn = gn+1i*hn; %偶数作为实部，奇数作为虚部
    Yk = fft(yn); %计算 fft
    [Gk,Hk] = csca(Yk); %分解为共轭对称与共轭反对称
    Hk = Hk./1i;
    Xk = Hk(mod(n,N/2)+1)+exp(-1i*2*pi*n/N).*Gk(mod(n,N/2)+1); %求出最后的 Xk
end

将上述代码保存为 nfft.m，然后与 matlab 自带的 fft 进行对比：

x = [1 2 3 4 5 6];
X_fft = fft(x)
X_nfft = nfft(x)

输出的结果为：

X_fft =

  1 至 3 列

  21.0000 + 0.0000i  -3.0000 + 5.1962i  -3.0000 + 1.7321i

  4 至 6 列

  -3.0000 + 0.0000i  -3.0000 - 1.7321i  -3.0000 - 5.1962i


X_nfft =

  1 至 3 列

  21.0000 + 0.0000i  -3.0000 + 5.1962i  -3.0000 + 1.7321i

  4 至 6 列

  -3.0000 - 0.0000i  -3.0000 - 1.7321i  -3.0000 - 5.1962i

两个结果一致，说明可用 单个 N 点 DFT 计算一个实序列的 2N 点 DFT.

信号频率估计

用采样率8000Hz，对频率为350Hz的单频正弦信号进行采样，取70个点作为原始信号：

fs = 8000;
f=350;
n = 0:69;
x = sin(2*pi*f*n./fs);

加入噪声。根据搜索到的资料，可以使用 matlab 内置的函数 awgn.m 来加入高斯白噪声：

x_noise = awgn(x,20,'measured');

为了方便后续进行测试，我们定义一个测试函数（FT.m，Frequent Test），输入频率估计方法，输出相应的均方误差：

function mse_result = FT(freq, x, snr, func,varargin)
%use func to estimate the frequent of a noise-corrupted signal, and compare it to the original freq, return mean-square-error of the estimation
% freq = original frequent
% x = original signal
% snr = sign noise ratio
% func = estimation function
% test_times = the times of test

    if ~exist('test_times', 'var') || isempty(test_times)
        % test_times 参数为空，或者不以变量的形式存在；
        test_times=100;
    end

    if ~exist('fs', 'var') || isempty(fs)
        % test_times 参数为空，或者不以变量的形式存在；
        test_times=100;
    end
    
    errors = zeros(1,test_times);
    for k = [1:test_times]
        x_noise = awgn(x, snr, 'measured');
        f_estimate = func(x_noise, fs);
        errors(k) = [errors f_estimate-freq];
    end
    mse_result = sum(errors.^2) / test_times;
end

下面来讨论不同的频率估计方法。首先，最简单的，就是直接求出 DFT 最大值处对应的频率（准确来说，是 DFT 前 $N/2$ 个点中最大值），这称为谱峰法。

function f_estm = f_estm_fft(xn, fs)
    Xk = abs(fft(xn));
    N = length(xn);
    [M,I]=max(Xk(1:ceil(N/2)));
    f_estm = (N/2-abs(N/2-(I-1)))*fs/N; %matlab 编号从1开始，故要减去1
end

测试代码如下（后面的测试代码都是类似的，只需要修改 test 对应的函数即可）

snr_array = [-5 0 5 10 20 inf];
errors = [];
test = @f_estm_fft;
for snr=snr_array
    errors = [errors log(FT(f, x, snr, test, 'fs',8000, 'test_times',1000))];
end
stem([-5 0 5 10 20 40], errors)
xlabel('snr/dB');
ylabel('log(mse)');
set(gca,'xtick',[-5 0 5 10 20 40]);
set(gca,'xticklabel',{'-5', '0', '5','10','20','inf'});

从下面的均方误差图可以看出，在信噪比较大的情况下，均方误差大约在 4 左右，而当信噪比较大时，均方误差就会升高：

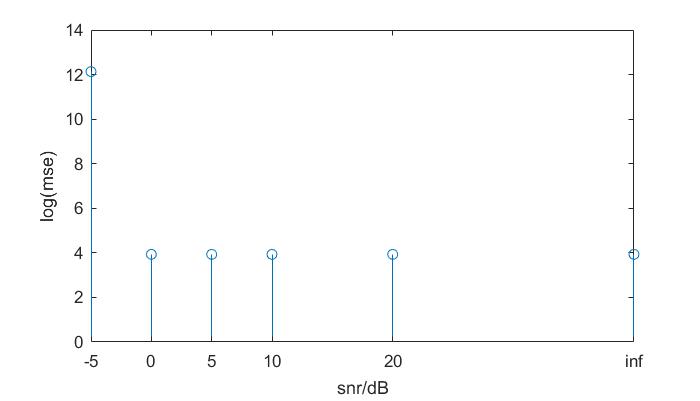
dft估计频率

上面的估计很简单，但存在一定误差。假设 DFT 幅度最大值的下标为 $k_p$，那么实际频率可以表示为：

$$ f = \frac{k_p+\delta}{N} f_s $$

我们的目标就是求出 $\delta$。常用的方法有：music算法，rife算法，周期图法，pisarenko,levenson法。下面利用 rife 算法，其表达式如下：

$$ \delta = \begin{cases} \dfrac{| X(k_p+1)|}{|X(k_p+1)|+|X(k_p)|}，|X(k_p+1)|>|X(k_p-1)|\\ \dfrac{-| X(k_p-1)|}{|X(k_p-1)|+|X(k_p)|}，|X(k_p+1)|\leq |X(k_p-1)| \end{cases} $$
function f_estm = f_estm_rife(xn, fs)
    Xk = abs(fft(xn));
    N = length(xn);
    [M,k0]=max(Xk(1:ceil(N/2)));
    
    p0=abs(Xk(k0));
    p1=abs(Xk(k0-1));
    p2=abs(Xk(k0+1));
    if p1>=p2
        pp=p1;flag=-1;
    else
        pp=p2;flag=1;
    end
    k=k0-1+flag*pp/(p0+pp);
    f_estm=k*fs/N;
end

使用相同的测试代码得到的图像如下，可以看出在信噪比越大，其估计的准确度越好。

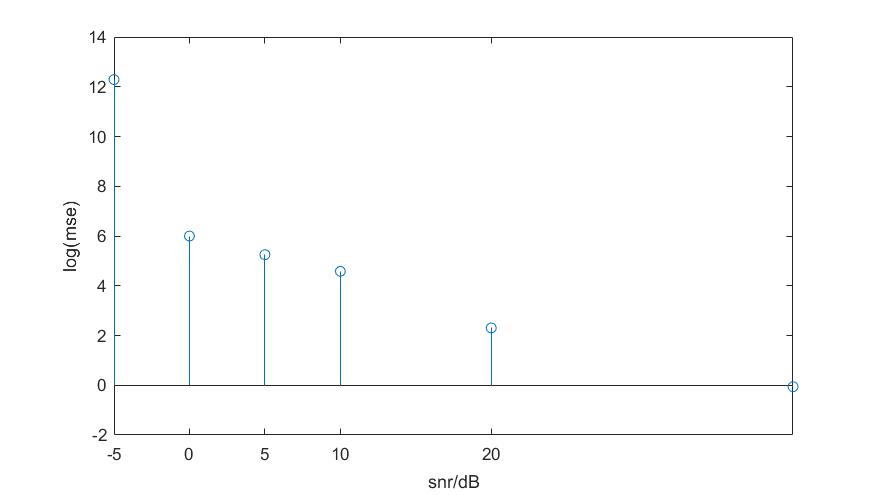
rife估计频率

另外还使用课堂中提到的导数法，其公式如下：

$$ \hat{\omega_c} = \frac{\sum_{k=0}^{N-1}|X_k|^2 k\omega_0}{\sum_{k=0}^{N-1}|X_k|^2}\approx \frac{\sum_{k=k_0-\Delta}^{k_0+\Delta}|X_k|^2 k\omega_0}{\sum_{k=k_0-\Delta}^{k_0+\Delta}|X_k|^2} $$
function f_estm = f_estm_dif(xn, fs)
    Xk = abs(fft(xn));
    N = length(xn);
    [M,k0]=max(Xk(1:ceil(N/2)));
    Delta=4;
    num=0;
    den=0;
    for k = [k0-Delta:k0+Delta]
        if k<1 || k>N
            continue
        end
        num=num+abs(Xk(k))^2.*(k-1);
        den=den+abs(Xk(k))^2;
    end
    f_estm=num*fs/(den*N);
end

使用相同的测试代码得到的图像如下，可以看出导数法在噪声较大与 rife 法类似，而在噪声较小时不如 rife 法，总体上仅比谱峰法好一点点。

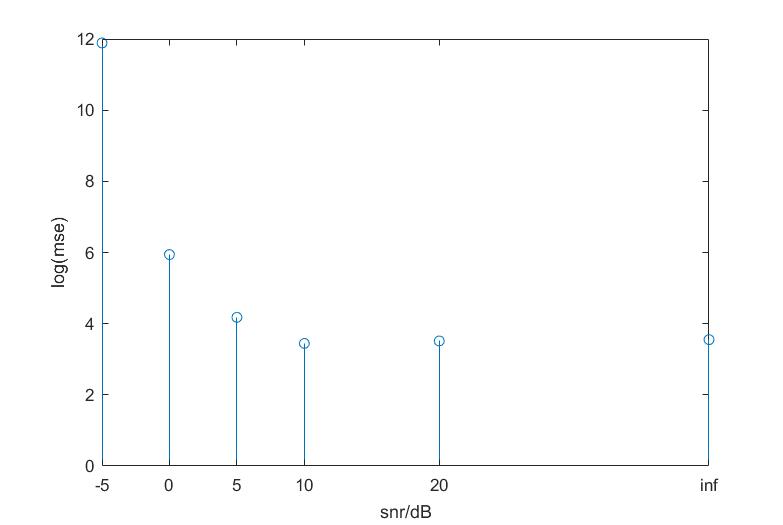
dif估计频率

总结：snr≤5时都不好，-5<snr<10 时谱峰法好，snr>10时rife法好啊👍

LFM脉冲压缩

说真的，我压根就不知道这是什么玩意，也没时间慢慢推导了，就直接参考了这篇文章：线性调频（LFM信号）脉冲压缩雷达matlab仿真，以及 基于MATLAB的线性调频信号的仿真

先是生成线性调频信号并加入噪声：

%%线性调频信号
T=10e-6;                                  %p脉冲持续时间10us
B=30e6;                                   %线性调频信号的频带宽度30MHz
K=B/T;                                      %调频斜率
Fs=2*B;Ts=1/Fs;                      %采样频率和采样间隔
N=T/Ts;
t=linspace(-T/2,T/2,N);
St=exp(j*pi*K*t.^2);                    %线性调频信号
St=awgn(St,10);
subplot(211)
plot(t*1e6,real(St));
xlabel('时间/us');
title('线性调频信号的实部');
grid on;axis tight;
subplot(212)
freq=linspace(-Fs/2,Fs/2,N);
plot(freq*1e-6,fftshift(abs(fft(St))));
xlabel('频率/MHz');
title('线性调频信号的幅频特性');
grid on;axis tight;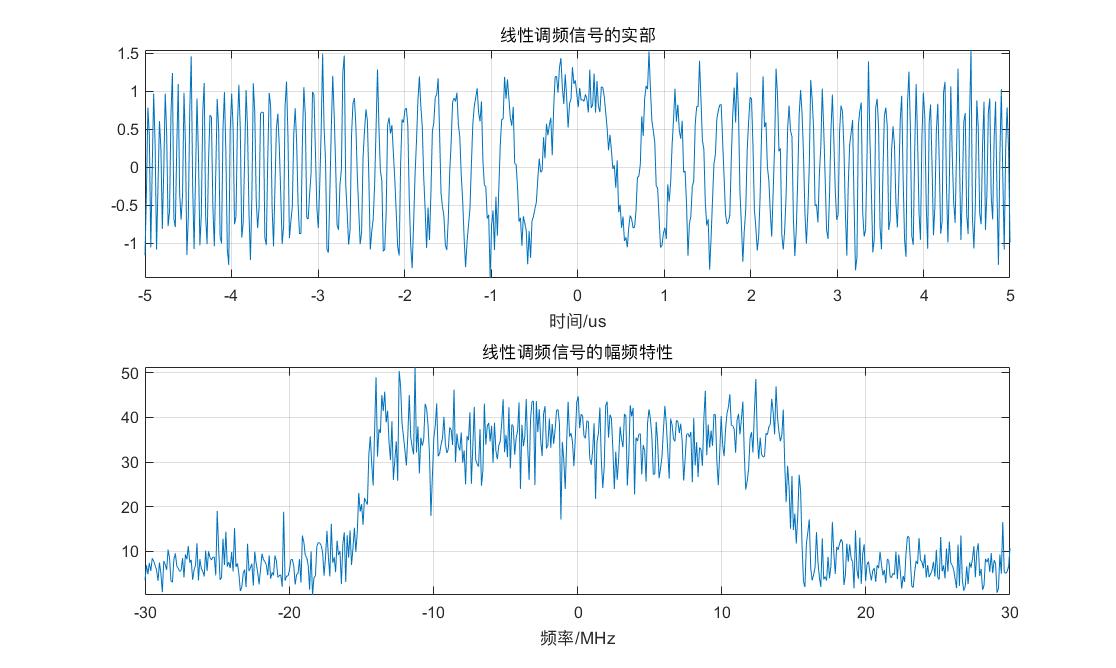

LTM with noise

%% 线性调频与脉冲压缩
clear,clc,close all
set(0,'defaultfigurecolor','w')
%% Chirp信号参数设置
Tr = 10e-6;%时宽
Br = 30e6;%带宽
Fs = 2*Br;%采样率
%% Chirp信号参数导出
Kr = Br/Tr;%调频率
N =  round( Tr / (1/Fs) );%采样点数
t = linspace( -Tr/2+0.1*Tr , Tr/2+0.1*Tr , N);%在[-Tp/2,Tp/2]选取采样点
%% Chirp信号生成
st = ( abs(t) < Tr/2 ) .* exp( 1j * pi * Kr * t.^2 );
st=awgn(st,10);
f_chirp= Kr * t; %信号频率
phase_chirp = pi * Kr * t.^2;%信号相位
%% 频谱
freq = linspace(-Fs/2,Fs/2,N);%频域采样
Sf = fftshift( fft(st) );
%% 时域匹配滤波
ht = conj( fliplr(st) ); %时域匹配滤波为发射信号时间反褶再取共轭
s1 = conv(st,ht); %线性调频信号经过匹配滤波器后的输出(时域卷积)
N1 = N+N-1 ;%线性卷积后信号长度变为 N1+N2-1
t1 = linspace( -Tr/2 , Tr/2 , N1);
% 时域匹配滤波
figure,plot( t1*1e6 , abs(s1) ),xlabel('t /us'),ylabel('幅度谱'),title('时间反褶取共轭，时域卷积');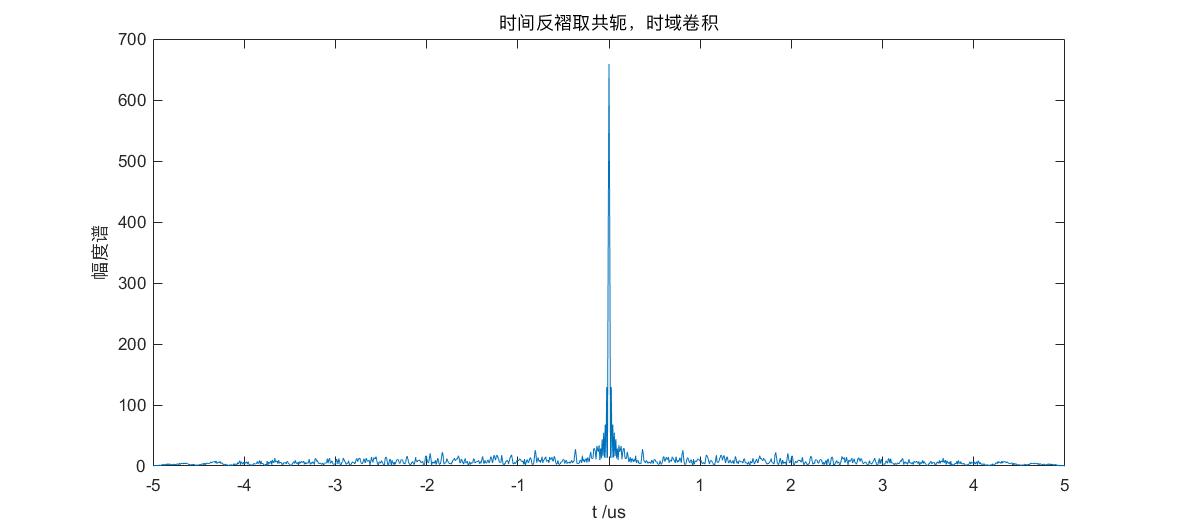

匹配滤波器

%%脉冲压缩 
clear; 
close all; 

T=10e-6; %时宽
B=30e6; %带宽
Rmin=8500;
Rmax=11500;
R=[9000,10000,10200];
RCS=[1 1 1];
C=3e8;
K=B/T;
Rwid=Rmax-Rmin;
Twid=2*Rwid/C;
Fs=5*B;Ts=1/Fs;
Nwid=ceil(Twid/Ts);
t=linspace(2*Rmin/C,2*Rmax/C,Nwid); 
M=length(R);
td=ones(M,1)*t-2*R'/C*ones(1,Nwid); 
SNR=[1,0.001];

for i=1:1:2
   Srt1=RCS*(exp(1i*pi*K*td.^2).*(abs(td)<T/2));
   n=sqrt(0.5*SNR(i))*(randn(size(Srt1))+1i*randn(size(Srt1))); %加噪声
   Srt=Srt1+n;
   Nchirp=ceil(T/Ts);
   Nfft=2^nextpow2(Nwid+Nwid-1);
   Srw=fft(Srt,Nfft);
   rw1=fft(Srt1,Nfft);
   t0=linspace(-T/2,T/2,Nchirp);
   St=exp(1i*pi*K*t0.^2);
   Sw=fft(St,Nfft);
   Sot=fftshift(ifft(Srw.*conj(Sw)));
   N0=Nfft/2-Nchirp/2;
   Z=abs(Sot(N0:N0+Nwid-1));
   figure
   subplot(211)
   plot(t*1e6,real(Srt));
   axis tight;
   xlabel('us');
   ylabel('幅度')
   title(['加噪线性调频信号压缩前,SNR =',num2str(-1*10*log10(SNR(i)))]); 
   subplot(212)
   plot(t*C/2,Z)
   xlabel('Range in meters');ylabel('幅度 ')
   title(['加噪线性调频信号压缩后,SNR =',num2str(-1*10*log10(SNR(i)))]); 
end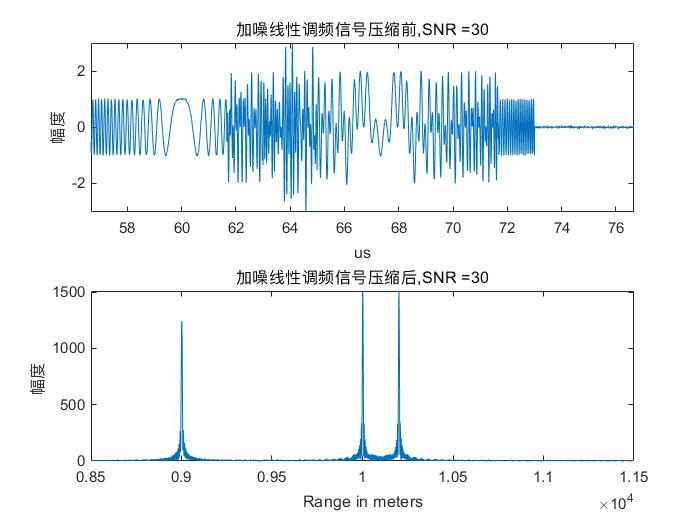

LTM1

LTM2

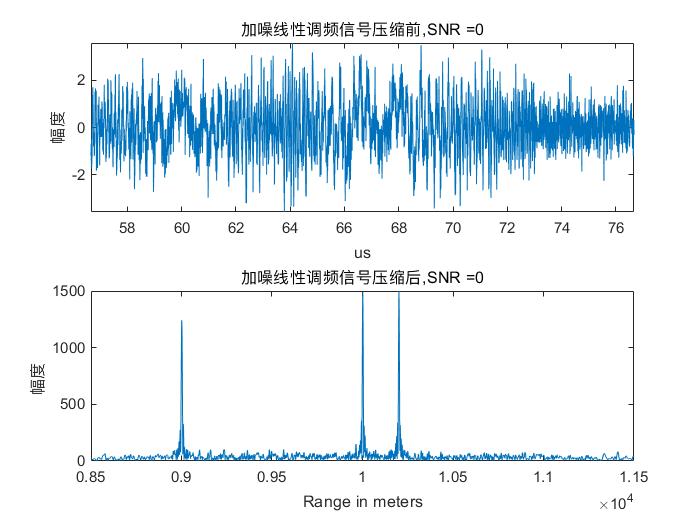
最后这个实验到底是什么鬼啊😥

离散傅里叶变换正交变换