系列
数字信号处理
5-有限长离散时间变换
离散傅里叶变换

离散傅里叶变换

$$ \begin{align*} \newcommand{\dif}{\mathop{}\!\mathrm{d}} \newcommand{\belowarrow}[1]{\mathop{#1}\limits_{\uparrow}} \newcommand{\bd}{\boldsymbol} \newcommand{\L}{\mathscr{L}} \newcommand{\xleftrightarrow}[1]{\stackrel{#1}{\longleftrightarrow}} \end{align*} $$

闲谈：按道理来说，离散傅里叶变换只涉及有限点运算，应该比无限点的 DTFT 好学，但学起来却晕得不行😵 究其原因，我在学习时是从 DTFT 入手的，遇到一些不同之处老是转不过来。

所以，我在网上找到了一份很详细的英语资料，从另一个方向学习 DFT。下面我就写写我学习过程中的笔记。

DFT 概述

对于长度为 $N$ 的序列 $x[n]$，其离散傅里叶变换 DFT 定义为：

$$ X[k] \triangleq \sum_{n=0}^{N-1} x[n] e^{-j\omega_k n} = \sum_{n=0}^{N-1} x[n] e^{-j 2\pi k n/N} $$

DFT 的引入

从几何引入 DFT

  我们可以将长度为 $N$ 的信号看做一个 $N$ 维向量 $x=[x_0,x_1,\cdots,x_{N-1}]$，每一个 $n$ 对应一个维度。

  我们可以定义向量的内积：

$$ \langle u,v\rangle \triangleq \sum_{n=0}^{N-1} u[n] v^*[n] $$

  我们可以很容易得出向量内积的几个性质：

  • $\langle u,u\rangle=\mathcal{E}_u$ （能量）
  • 共轭对称性：$\langle u,v\rangle =\langle v,u\rangle ^*$
  • 线性性：
    • $\langle \alpha u+\beta v,w\rangle = \alpha\langle u,w \rangle +\beta\langle v,w \rangle$
    • $\langle u,\alpha v+\beta w \rangle = \alpha\langle u,v \rangle +\beta\langle u,w \rangle$

  我们可以用内积定义向量的范数：

$$ \|u\| \triangleq \sqrt{\langle u,u\rangle}=\sqrt{\sum_{n=0}^{N-1} u[n]u^*[n]} $$

  有了内积和范数，就可以得到向量的投影：

$$ P_x(y) \triangleq \frac{\langle y,x\rangle}{\|x\|^2} x $$

  上式表示向量 $y$ 在 $x$ 上的投影。有了投影，我们就可以得到信号的正交分解：

$$ x = \sum_{n=0}^{N-1} \alpha_n s_n\\ \alpha_n = P_{s_n}(x) $$

  其中，$\{s_n\}$ 是一组正交基，满足：

$$ P_{s_k}(s_l) \triangleq \frac{\langle s_l, s_k \rangle}{\|s_k\|^2} s_k = \begin{cases} 0, & l\neq k\\ s_k, & l = k \end{cases} $$

  我们都知道不同频率的正弦信号在一个周期内相互正交（如果时长不是整周期，则不正交），比如：

$$ x_1[n]=A_1 \sin( \frac{2\pi k_1}{N} n)\\ x_2[n]=A_2 \sin( \frac{2\pi k_2}{N} n)\\ k_1,k_2 \in \mathbb{Z}\,且\,0\leq k_1,k_2\lt N\\ $$$$ \begin{align} \langle x_1,x_2 \rangle &= \sum_{n=0}^{N-1} x_1x_2\\ &=A_1A_2 \sum_{n=0}^{N-1} \sin( \frac{2\pi k_1}{N} n) \sin( \frac{2\pi k_2}{N} n)\\ &=\frac{A_1A_2}{2} \sum_{n=0}^{N-1} \left[ \cos\left(\frac{2\pi k_1}{N} n-\frac{2\pi k_2}{N} n\right)-\cos\left(\frac{2\pi k_1}{N} n+\frac{2\pi k_2}{N} n\right) \right]\\ &=\frac{A_1A_2}{2} \sum_{n=0}^{N-1} \left\{ \cos\left[\frac{2\pi}{N}(k_1-k_2) n\right]-\cos\left[\frac{2\pi}{N} (k_1+k_2)n\right] \right\}\\ &= \begin{cases} 0, & k_1\neq k_2\\ \frac{A_1A_2N}{2}, & k_1=k_2 \end{cases} \end{align} $$

  如果我们以 $f_s$ 对 $x(t)$ 采样得到 $N$ 点 $x[n]$，根据上面的证明，我们能取的谐波频率只能是：

$$ f_k = \frac{k}{N} f_s, \; k=0,1,2,\cdots,N-1 $$

  于是我们构造如下一组正交基（从正弦推广到e指数）：

$$ s_k[n]\triangleq e^{j \omega_k nT}=e^{j 2\pi kn/N}\\ \omega_k \triangleq 2\pi f_k= 2\pi k\frac{f_s}{N}，T=\frac{1}{f_s} $$

  为了偷懒，我们定义 $W_N=e^{-j2\pi/N}$，因此 $s_k=W_N^{-k}$。有趣的是，这一组正交基正好均分复平面上的单位圆（如下图所示）。

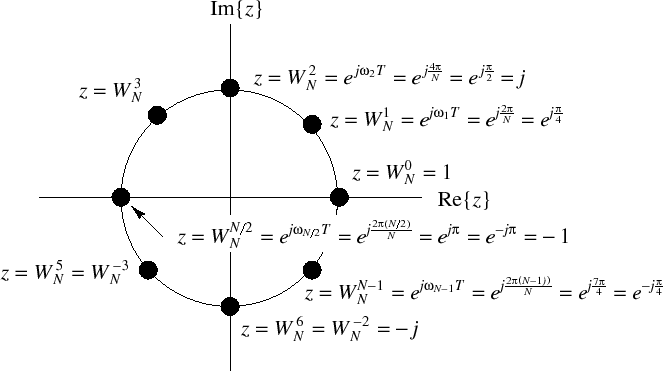
  我们可以证明这是一组正交基：

$$ \begin{align} \langle s_k,s_l \rangle &\triangleq \sum_{n=0}^{N-1} s_k[n] s_l^*[n]\\ &=\sum_{n=0}^{N-1} e^{j2\pi (k-l) n/N}\\ &=\frac{1-e^{j2\pi(k-l)}}{1-e^{j2\pi(k-l)/N}}\\ &= \begin{cases} 0 & k\neq l\\ N & k=l \end{cases} \end{align} $$

  我们进一步对 $s_k$ 进行正则化：

$$ \tilde{s}_k[n] \triangleq \frac{s_k[n]}{\sqrt{N}}\\ \langle \tilde{s}_k,\tilde{s}_l \rangle = \begin{cases} 0 & k\neq l\\ 1 & k=l \end{cases} $$

  信号在 $\tilde{s}_k$ 上的投影就是 NDFT（Normalized DFT），信号在 $s_k$ 上的投影的 $N$ 倍就是 DFT：

$$ X[k] \triangleq \langle x,s_k \rangle \triangleq \sum_{n=0}^{N-1} x[n] s_k^*[n] \quad k=0,1,\cdots,N-1\\ 其中，s_k[n] \triangleq e^{j 2\pi kn/N} $$

   $x$ 在 $s_k$ 上的投影为：

$$ \frac{\langle x,s_k\rangle}{\|s_k\|^2}=\frac{X[k]}{N} $$

  要从投影恢复回原信号，我们只需要将分解后的向量相加，注意到DFT实际是投影的 $N$ 倍，所以还需要除以 $N$：

$$ x[n]=\frac{1}{N}\sum_{k=0}^{N-1} X[k] e^{j 2\pi kn/N} $$

从抽样引入 DFT

  回忆我们对模拟信号进行采样的过程，经过采样后，频域进行了周期性延拓。同理，如果我们对频域进行采样，那么时域也进行周期性延拓，证明如下：我们先求解 $\delta[n-kN]$ 的离散时间傅里叶变换：

$$ \begin{align} a_k &= \frac{1}{N}\sum_{n=\langle N \rangle} \delta[n-kN] e^{-jk\omega_0n} \\ &= \frac{1}{N} \sum_{n=0}^{N-1} \delta[n-kN] e^{-jk\omega_0n}\\ &= \frac{1}{N} \\ \end{align}\\ $$$$ \begin{align} X(e^{j\omega}) &=\sum_{k=-\infty}^{+\infty} 2\pi a_k \delta(\omega-\frac{2\pi k}{N})\\ &= \frac{2\pi}{N} \sum_{k=-\infty}^{+\infty} \delta(\omega-\frac{2\pi k}{N}) \end{align} $$

  由于时域卷积对应频域相乘，故如果在频域上 $[0,2\pi]$ 内取 $N$ 点，则时域上会以 $N$ 为周期。结合离散时间傅里叶变换（DTFT）：

$$ 分析公式：X(e^{j\omega})=\sum_{n=-\infty}^{+\infty} x[n] e^{-j\omega n}\\ 综合公式：x[n]=\frac{1}{2\pi} \int_{2\pi} X(e^{j\omega}) e^{j\omega n} \dif \omega $$

  我们可以得到离散傅里叶变换（DFT）：

$$ X[k] \triangleq \sum_{n=0}^{N-1} x[n] e^{-j \frac{2\pi k}{N} n}\\ x[n]=\frac{1}{N}\sum_{k=0}^{N-1} X[k] e^{j \frac{2\pi k}{N} n} $$

  把 $\omega$ 替换成 $\frac{2\pi k}{N}$ 的过程就相当于在频域取样。为了偷懒，我们定义 $W_N=e^{-j2\pi/N}$，并改写为：

$$ X[k] \triangleq \sum_{n=0}^{N-1} x[n] W_N^{kn}\\ x[n]=\frac{1}{N}\sum_{k=0}^{N-1} X[k] W_N^{-kn} $$

  从 $X[k]$ 恢复成 $X(e^{j\omega})$ 则是通过插值来实现：

$$ \begin{align} X(e^{j\omega}) &= \sum_{n=0}^{N-1} \left\{ \frac{1}{N}\sum_{k=0}^{N-1} X[k] W_N^{-kn} \right\} e^{-j\omega n}\\ &= \frac{1}{N} \sum_{k=0}^{N-1} X[k] \sum_{n=0}^{N-1} e^{j \frac{2\pi k}{N} n} e^{-j\omega n}\\ \end{align} $$$$ \begin{align} \sum_{n=0}^{N-1} e^{j \frac{2\pi k}{N} n} e^{-j\omega n} &= \frac{1-e^{-j(\omega N - 2\pi k)}}{1-e^{-j(\omega - 2\pi k/N)}}\\ &= \frac{e^{-j[(\omega N - 2\pi k)/2]}}{e^{-j[(\omega N - 2\pi k)/2N]}} \frac{\sin \left( \frac{\omega N-2 \pi k}{2} \right)}{\sin \left( \frac{\omega N-2 \pi k}{2N} \right)}\\ &= \frac{\sin \left( \frac{\omega N-2 \pi k}{2} \right)}{\sin \left( \frac{\omega N-2 \pi k}{2N} \right)} e^{-j[\omega - (2\pi k/N)][(N-1)/2]} \end{align} $$

我们定义插值函数为 $\Phi (\omega)$：

$$ \begin{align} \Phi(\omega) &= \frac{\sin \left( \frac{\omega N}{2} \right)}{N \sin \left( \frac{\omega}{2} \right)} e^{-j\omega [(N-1)/2]} \end{align}\\ 特殊的，\Phi(\omega)\Big|_{\omega=2\pi k/N} = \begin{cases} 1, & k=0\\ 0, & 1\leq k \leq N-1 \end{cases} $$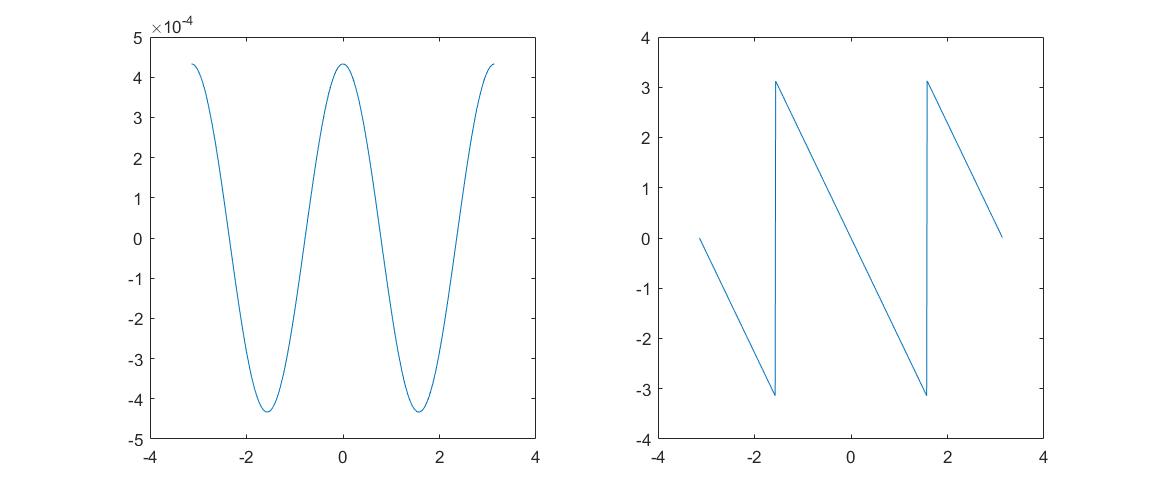

则插值过程能表示成：

$$ X(e^{j\omega}) = \sum_{k=0}^{N-1} X[k] \Phi\left( \omega - \frac{2\pi k}{N} \right) $$

频谱泄露

  从采样的角度去理解的话，对于那些介于采样点之间的频率，从直觉上来讲是无法得到的，但并非如此。

  我们可以假设任意一个正弦信号：$x[n]=e^{j\omega_x nT}$，将它与正交基做内积：

$$ \begin{align} X(\omega_k) &= \langle x,s_k^* \rangle\\ &= \sum_0^{N-1} e^{j\omega_x nT} e^{-j\omega_k nT}\\ &= \sum_0^{N-1} e^{j(\omega_x-\omega_k) nT}\\ &= \frac{1-e^{j(\omega_x-\omega_k) NT}}{1-e^{j(\omega_x-\omega_k) T}}\\ &= e^{j(\omega_x-\omega_k)(N-1)T/2} \frac{\sin[(\omega_x-\omega_k)NT/2]}{\sin[(\omega_x-\omega_k)T/2]} \end{align} $$

  显然，当 $\omega_x=\omega_k$ 时，$X(\omega_k)=N$；而当 $\omega_x\neq\omega_k$ 时，有：

$$ |X(\omega_k)|=\left|\frac{\sin[(\omega_x-\omega_k)NT/2]}{\sin[(\omega_x-\omega_k)T/2]}\right| $$

  我们之前定义过：

$$ \omega_k \triangleq 2\pi k\frac{f_s}{N}= 2\pi k\frac{1}{TN},\;k=0,1,\cdots,N-1 $$

我们不妨取 $N=16$，$x=N/5$（也就是 $\omega_x = 2 \pi \frac{N}{5} \frac{f_s}{N}$），作出图像：

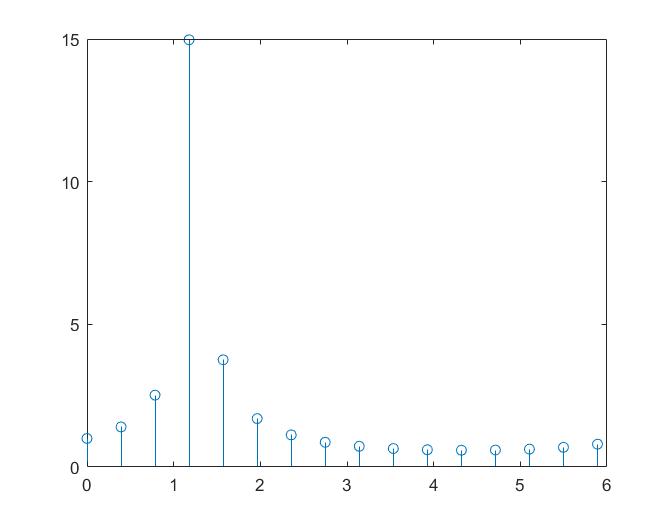
我们可以看到，最靠近 $N/5$ 的谱线，也就是 $k=N/4=4$ 的谱线是最高的，另外，其他谱线也有一定的值。这就叫 频谱泄露。

  上面是通过公式推导得到的，我们可以用 matlab 来进行验证，最终画出来的图像是一样的。

fs=1;
N=16;
x=N/5;
wx=2*pi*x*fs;
n=[0:N-1];
xn=exp(j*wx*n);
wn=2*pi*n/N;
stem(wn,abs(fft(xn)));

常见 DFT 变换对

$$ \sum_{k=-\infty}^\infty \delta[n+Nk] = \left\{ \begin{array}{ll} 1, & \text{ if } n=0, \pm N, \pm 2N , \ldots\\ 0, & \text{ else.} \end{array}\right.\\ \xleftrightarrow{DFT} 1 \;(\text{period} N) $$$$ e^{j2\pi k_0 n/N} \xleftrightarrow{DFT} N\delta[\langle k - k_0\rangle_N] $$$$ \cos(\frac{2\pi}{N}k_0n) \xleftrightarrow{DFT} \frac{N}{2}(\delta[\langle k - k_0\rangle_N] + \delta[\langle k - k_0\rangle_N]) $$

DFT 的性质

线性性

$$ \alpha g[n] + \beta h[n] \xleftrightarrow{\text{DFT}} \alpha G[k] + \beta H[k] $$

这个没啥好说的，证明方法和之前傅里叶变换一样。

圆周时移

  由于 DFT 本质上是对原信号在时域上进行周期延拓，那么当信号进行时移变换时，实际上是在进行“圆周平移”。

$$ g[\langle n-n_0 \rangle_N] \xleftrightarrow{\text{DFT}} W_N^{kn_0} G[k] $$

  当然，我们也可以简单证明一下：

$$ \begin{align} \sum_{n=0}^{N-1} x[\langle n-n_0 \rangle_N] W_N^{kn} &= \sum_{n=0}^{N-1} x[\langle n-n_0 \rangle_N] W_N^{k(n-n_0+n_0)}\\ &= W_N^{kn_0} \sum_{n=0}^{N-1} x[\langle n-n_0 \rangle_N] W_N^{k(n-n_0)}\\ &= W_N^{kn_0} X[k] \end{align} $$

圆周频移

$$ W_N^{-k_0 n} g[n] \xleftrightarrow{\text{DFT}} G[\langle k-k_0 \rangle_N] $$

对称性

序列DFT
$x[n]=x_\text{re}[n]+j x_\text{im}[n]$$X[k]=X_\text{re}[k]+j X_\text{im}[k]$
$x^*[n]$$X^*[\langle-k\rangle_N]$
$x^*[\langle-n\rangle_N]$$X^*[k]$
$x_\text{re}[n]$$X_\text{cs} =\frac{1}{2} \{ X[k]+X^*[\langle -k \rangle_N] \}$
$j x_\text{im}[n]$$X_\text{ca}[k]=\frac{1}{2} \{ X[k]-X^*[\langle -k \rangle_N] \}$
$x_\text{cs}[n]$$X_\text{re}[k]$
$x_\text{ca}[n]$$jX_\text{im}[k]$

乍一看好像很复杂，我们来看看看第 2 条式子的证明👀：

$$ \begin{aligned} \sum_{n=0}^{N-1} x^*[n] e^{-\frac{2\pi kn}{N}} &= \left\{ \sum_{n=0}^{N-1} x[n] e^{2\pi kn/N} \right\}^*\\ &= \left\{ \sum_{n=0}^{N-1} x[n] e^{-2\pi (-k)n/N} \right\}^*\\ &= \left\{ \sum_{n=0}^{N-1} x[n] e^{-2\pi \langle -k\rangle_N n/N} \right\}^*\\ &= X^*[\langle-k\rangle_N] \end{aligned} $$

第 3 条也是类似的。然后由 2、3 就能推导出后面的。

对称性可以用于简化某些特殊的 DFT 计算，考试中比较喜欢考的就是：有一个 $2N$ 长的实序列，要求用 $N$ 长的 FFT 进行计算（可以用其他简单的辅助运算），过程如下：

圆周卷积定理

$$ g[n] Ⓝ h[n] \xleftrightarrow{DFT} G[k]H[k] $$

直接证明太麻烦了，可以从 DTFT 的卷积性质推导，然后再采样就行。总而言之，凡是看到“圆周”，就要想到对周期信号进行采样。

调制定理

$$ g[n]h[n] \xleftrightarrow{DFT} \frac{1}{N} \sum_{\ell=0}^N G[\ell]H[\langle k-\ell \rangle_N] $$

上一条定理的对偶定理。

对偶定理

$$ g[n] \xleftrightarrow{DFT} G[k]\\ G[n] \xleftrightarrow{DFT} N g[\langle -k \rangle_N] $$

这个证起来不难，我就说个大概吧（其实是想偷懒）

  • 对 $G[n]$ 进行 DFT
  • 先代入 $g[n]$
  • 再交换求和顺序
  • 变量代换（引入了圆周时反）
  • 化简，化简时会用到一条关系式（引入了 $N$）：
$$ \sum_{n=0}^{N-1} W_N^{kn} = \begin{cases} N, & k=0\\ 0, & k\neq 0 \end{cases} $$
懒得自己算的同学请点击展开
$$ \begin{aligned} \sum_{n=0}^{N-1} G[n] W_N^{kn} &= \sum_{n=0}^{N-1} \left\{ \sum_{m=0}^{N-1} g[m] W_N^{nm} \right\} W_N^{kn}\\ &= \sum_{m=0}^{N-1} \left\{ \sum_{n=0}^{N-1} g[m] W_N^{n(m+k)} \right\}\\ {}^{(\ell=m+k)}&= \sum_{\ell=0}^{N-1} \left\{ \sum_{n=0}^{N-1} g[\langle \ell - k \rangle_N] W_N^{n\ell } \right\}\\ &=N [\langle- k \rangle_N] \end{aligned} $$

Parseval 定理

$$ \sum_{n=0}^{N-1} g[n]h^*[n]=\frac{1}{N} \sum_{k=0}^{N-1} G[k]H^*[k]\\ 特殊的，\sum_{n=0}^{N-1} |g[n]|^2 =\frac{1}{N} \sum_{k=0}^{N-1} |G[k]|^2 $$

证明方法嘛，先将 $h[n]$ 用 $H[k]$ 表示（这一步引入了 $1/N$），然后利用共轭使得 $W_{N}^{-kn}$ 变为 $W_{N}^{kn}$，然后交换求和顺序，再把 $g[n]$ 变成 $G[k]$。

习题

Tip

5.8 求长度为 $N$ 的如下序列的 $N$ 点 DFT：
（a）$x_a[n]=\cos (2 \pi n /N)$
（b）$x_b[n]=\sin^2(2 \pi n/N)$
（c）$x_c[n]=\sin^3 (2 \pi n/N)$

Note

解：由于是三角函数，所以首先想到的是写成 $e$ 指数的形式再求解。

$$ \begin{aligned} x_a[n]&=\frac{1}{2}\left( e^{j2 \pi n /N}+e^{-j2 \pi n /N} \right)\\ x_b[n]&=\frac{1-\cos(2 \pi 2n /N)}{2}=\frac{1-\frac{1}{2}\left( e^{j2 \pi 2n /N}+e^{-j2 \pi 2n /N} \right)}{2}\\ x_c[n]&=\frac{1}{4}[3 \sin(2 \pi n/N)-\sin (2 \pi 3n/N)]\\ &=\frac{1}{4}\left[ \frac{3}{2j}\left( e^{j2 \pi n /N}-e^{-j2 \pi n /N} \right) - \frac{1}{2j}\left( e^{j2 \pi 3n /N}-e^{-j2 \pi 3n /N} \right) \right] \end{aligned} $$

根据常用 DFT 变换对 $e^{j2\pi k_0 n/N}\xleftrightarrow{DFT}N\delta(\langle k - k_0\rangle_N)$，可以直接写出：

$$ \begin{aligned} X_a[k]&=\frac{N}{2} \left[\delta(\langle k - 1\rangle_N)+\delta(\langle k + 1\rangle_N)\right]\\ X_b[k]&=\frac{1-\frac{N}{2} \left[\delta(\langle k - 2\rangle_N)+\delta(\langle k + 2\rangle_N)\right]}{2}\\ x_c[k]&=\frac{1}{4}\left[ \frac{3}{2j}\Big( \delta(\langle k - 1\rangle_N)-\delta(\langle k + 1\rangle_N)\Big)\\- \frac{1}{2j}\Big( \delta(\langle k - 3\rangle_N)-\delta(\langle k + 3\rangle_N)\Big) \right] \end{aligned} $$

Tip

5.14 设 $X[k]$ 是长为 $N$ 的序列 $x[n]$ 的 $N$ 点 DFT，$N$ 为偶数。定义两个长度为 $\frac{N}{2}$ 的序列为：

$$ \displaylines{ g[n] = \frac{1}{2}(x[2n]+x[2n+1])\\ h[n] = \frac{1}{2}(x[2n]-x[2n+1])\\ 0\leq n \leq \frac{N}{2}-1 } $$


若 $g[n]$,$h[n]$ 的 $N/2$ 点 DFT 分别是 $G[n]$,$H[n]$，请用 $G[n],H[n]$ 求 $X[n]$

[!NOTE] 解：这题显然是考 DIT-FFT，根据 DIT-FFT 的公式，可以写出：

$$ \begin{aligned} X[k]&=\sum_{r=0}^{N/2-1} x[2r] (W_N^{2})^{kr}+W_N^{k} \sum_{r=0}^{N/2-1} x[2r+1] (W_N^{2})^{kr}\\ &=\sum_{r=0}^{N/2-1} x[2r] W_{N/2}^{kr}+W_N^{k} \sum_{r=0}^{N/2-1} x[2r+1] W_{N/2}^{kr}\\ &= (G[k]+H[k])+W_N^k (G[k]-H[k]) \quad k=0,1,\cdots,N-1 \end{aligned} $$
$$ X[k+\frac{N}{2}] = (G[k]+H[k])-W_N^k (G[k]-H[k]) \quad k=0,1,\cdots,N-1 $$

[!TIP] 5.48 序列 $\{x[n]\}=\{2,-3,1,4\}$，$0\leq n \leq3$，与下面定义在 $0\leq n \leq3$ 进行 4 点圆周卷积：

$$ \displaylines{ \{h_1[n]\}=\{1,4,-2,-3\}\\ \{h_2[n]\}=\{5,4-4,-1,3\}\\ \{h_3[n]\}=\{-2,5,2,-4\}\\ \{h_4[n]\}=\{-3,2,-3,4\} } $$

计算结果如下：

$$ \displaylines{ \{y_a[n]\}=\{-16,-24,27,25\}\\ \{y_b[n]\}=\{-13,5,1,7\}\\ \{y_c[n]\}=\{30,20,-29,-17\}\\ \{y_d[n]\}=\{25,-6,-27,8\}\\ } $$

不计算圆周卷积，将结果与圆周卷积配对。

[!NOTE] 解：可以通过求 DFT 来求圆周卷积，不过太麻烦了。可以进行求和：

$$ \displaylines{ \sum_{n=0}^{N-1} x[n]=4\\ \sum_{n=0}^{N-1} h_1[n]=0 \quad \sum_{n=0}^{N-1} y_a[n]=12\\ \sum_{n=0}^{N-1} h_2[n]=3 \quad \sum_{n=0}^{N-1} y_b[n]=0\\ \sum_{n=0}^{N-1} h_3[n]=1 \quad \sum_{n=0}^{N-1} y_c[n]=4\\ \sum_{n=0}^{N-1} h_4[n]=0 \quad \sum_{n=0}^{N-1} y_d[n]=0 } $$

由于 $\sum x \cdot \sum h_2 = \sum y_a$ 和 $\sum x \cdot \sum h_3 = \sum y_c$，所以我们可以判断出：

$$ x Ⓝ h_2 = y_a\\ x Ⓝ h_3 = y_c $$

还有俩个判断不了，我们可以进行交替求和：

$$ \displaylines{ \sum_{n=0}^{N-1} (-1)^n x[n]=2\\ \sum_{n=0}^{N-1} (-1)^n h_1[n]=-2 \quad \sum_{n=0}^{N-1} (-1)^n y_b[n]=-24 \\ \sum_{n=0}^{N-1} (-1)^n h_4[n]=-12 \quad \sum_{n=0}^{N-1} (-1)^n y_d[n]=-4 } $$

由于 $\sum (-1)^n x \cdot \sum (-1)^n h_1 = \sum (-1)^n y_d$ 和 $\sum (-1)^n x \cdot \sum (-1)^n h_4 = \sum (-1)^n y_b$，所以我们可以判断出：

$$ x Ⓝ h_1 = y_d\\ x Ⓝ h_4 = y_b $$

[!TIP] 5.51 偶数长 $x[n]$ 的 DFT 为 $X[k]$，用 $X[k]$ 表示下列序列的 $N$ 点 DFT

$$ \begin{aligned} u[n]&=x[n]-x[\langle n-\frac{N}{2} \rangle_N]\\ v[n]&=x[n]+x[\langle n- \frac{N}{2}\rangle_N]\\ y[n]&=(-1)^n x[n] \end{aligned} $$

Note

解：考察的是 DFT 的性质。

$$ U[k]=X[k]-(-1)^k X[k]\\ V[k]=X[k]+(-1)^k X[k]\\ Y[k]=X[\langle k- \frac{N}{2}\rangle_N] $$
FFT离散傅里叶变换实验