频域中的离散时间信号
$$ \begin{align*} \newcommand{\dif}{\mathop{}\!\mathrm{d}} \newcommand{\belowarrow}[1]{\mathop{#1}\limits_{\uparrow}} \newcommand{\bd}{\boldsymbol} \newcommand{\L}{\mathscr{L}} \newcommand{\xleftrightarrow}[1]{\stackrel{#1}{\longleftrightarrow}} \end{align*} $$傅里叶变换
连续
如果连续时间信号满足满足 $\int_{-\infty}^{+\infty} \vert x(t)\vert^2\dif t< \infty$ 或满足 狄利克雷条件(如下):
- 在有限区间内,不连续点有限,且极值数目有限
- 绝对可积:$\int_{-\infty}^{+\infty} \vert x(t) \vert \dif t< \infty$
那么,该信号有 CTFT(Continuous Time Fourier Transform):
$$ \displaylines{ x_a(t) \xleftrightarrow{\text{CTFT}} X_a(j\Omega)\\ X_a(j\Omega) = \int_{-\infty}^{+\infty} x_a(t) e^{-j\Omega t} \dif t\\ x_a(t)=\frac{1}{2\pi} \int_{-\infty}^{+\infty} X_a(t) e^{j\Omega t} \dif \Omega } $$离散
如果离散时间信号满足 $\sum_{n=-\infty}^{+\infty} \vert x [n]\vert < \infty$ 或 $\sum_{n=-\infty}^{+\infty} \vert x [n]\vert^2 < \infty$,那么该信号有 DTFT(Discrete Time Fourier Transform):
$$ \displaylines{ x[n] \xleftrightarrow{\text{DTFT}}X(e^{j\omega})\\ 分析公式:X(e^{j\omega})=\sum_{n=-\infty}^{+\infty} x[n] e^{-j\omega n}\\ 综合公式:x[n]=\frac{1}{2\pi} \int_{2\pi} X(e^{j\omega}) e^{j\omega n} \dif \omega } $$由于本门课程主要是讨论离散信号,所以我们将 DTFT 简写为 $\mathcal{F}$(这点与我之前写的信号与系统的笔记不同),即:
$$ x[n] \xleftrightarrow{\mathcal{F}}X(e^{j\omega}) $$离散时间傅里叶变换的性质请看 信号与系统 - 离散时间傅里叶变换的性质,比较重要的有:线性、时间反转、时移、频移、共轭对称、时域/频域卷积、微分、Pasewal定理等。同时还要理解这些变换的含义。
傅里叶变换中有很多对称关系,比如(以下都是要记牢的):
| 前提 | 序列 | 傅里叶变换 | 序列 | 傅里叶变换 |
|---|---|---|---|---|
| 实序列 | $x_\text{ev}[n]$ | $X_\text{re}(e^{j\omega})$且为偶 | $x_\text{od}[n]$ | $jX_\text{im}(e^{j\omega})$且为奇 |
| 复序列 | $x_\text{re}[n]$ | $X_\text{cs}(e^{j\omega})$ | $jx_\text{im}[n]$ | $X_\text{ca}[n]$ |
| 复序列 | $x_\text{cs}[n]$ | $X_\text{re}(e^{j\omega})$ | $x_\text{ca}[n]$ | $jX_\text{im}[n]$ |
采样定理
低通信号的采样
在信号与系统中已经推导过,这里直接给出结论:若采样频率大于信号最高频的 2 倍时,可以由采样信号无失真地恢复出原信号。这里要注意的是等于 2 倍是不行的,至于为什么,你考虑一下正弦信号就知道了。
带通信号的采样
假设 $x(t)$ 的频谱范围为 $\omega_l \leq \vert \omega \vert \leq \omega_h$,带宽为 $B_\omega=\omega_h - \omega_l$。经过采样后,频谱会以采样频率 $\omega_s$ 进行周期性平移:$\omega_l+n\omega_s \leq \vert \omega \vert \leq \omega_h+n\omega_s$。要使频谱不发生混叠(负半轴的频谱向右平移 $n-1$ 次与 $n$ 次后不会与正半轴的频谱重叠),则要满足:
$$ \begin{cases} -\omega_l+(n-1)\omega_s \lt \omega_l\\ -\omega_h+n\omega_s \lt \omega_h \end{cases} $$$$ \Rightarrow \frac{2\omega_h}{n}\lt \omega_s \lt \frac{2\omega_l}{n-1} $$那么 $n$ 的取值是不是随便取呢?显然不是。首先我们考虑下界,根据上面的式子有 $n \gt \dfrac{2\omega_h}{\omega_s}$,再根据 Nyquist 采样定理(低通采样定理),$\omega_s > 2\omega_h$ 且 $\omega_s \neq 2\omega_h$ 时频谱不会混叠,所以 $n\geq 2$;我们再考虑上界,显然,在 $(-\omega_l,\omega_l)$ 内最多平移 $\lfloor \dfrac{\omega_l}{B_\omega} \rfloor$ 次,故 $n-1 \leq \lfloor \dfrac{\omega_l}{B_\omega} \rfloor$,即 $n \leq \lfloor \dfrac{\omega_l}{B_\omega} \rfloor +1 = \lfloor \dfrac{\omega_h}{B_\omega} \rfloor$
当 $n$ 取 $2 \leq n \leq \lfloor \dfrac{\omega_h}{B_\omega} \rfloor$ 中的一系列整数,能得到一系列 $\omega_s$ 的取值范围。为了说明这点,我们不妨假设 $\omega_h=kB_\omega$,于是上面的式子可以简化为:
$$ 2 \leq n \leq k $$$$ \frac{2kB_\omega}{n}\lt \omega_s \lt \frac{2(k-1)B_\omega}{n-1} $$| $\omega_h=kB_\omega$ | $n=1$ | $n=2$ | $n=3$ | $n=4$ |
|---|---|---|---|---|
| $\omega_h=1B_\omega$ | $(2B_\omega,\infty)$ | |||
| $\omega_h=2B_\omega$ | $(4B_\omega,\infty)$ | $2B_\omega$❌ | ||
| $\omega_h=3B_\omega$ | $(6B_\omega,\infty)$ | $(3B_\omega,4B_\omega)$ | $2B_\omega$❌ | |
| $\omega_h=4B_\omega$ | $(8B_\omega,\infty)$ | $(4B_\omega,6B_\omega)$ | $(\frac{8}{3}B_\omega,3 B_\omega)$ | $2B_\omega$❌ |
注:关于 $2B_\omega$ 的那些网格,书上认为可以用这个频率来采样。但从公式中很明显看出此时频谱的边上会发生混叠,因此我个人认为不能取 $2B_\omega$
从上面可以看出,$k$ 越大,可选择的频段越多。我们将 $\dfrac{B_\omega}{\omega_h}$ 定义为 相对带宽 $B_R$,换句话说,相对带宽越小,可选择的频段越多,采样频率也比Nyquist采样频率更小。在实际中,很多信号都是带通信号(如蜂窝电话在900MHz上仅占30kHz),此时我们只需要用相对低频的采样频率即可完成无失真采样。
如果最高频率非带宽的整数倍,向左或向右扩展后,使最高频率是新带宽 $B'$ 的整数倍,则采样频率需大于$2B'$。
本章练习题
Tip
3.18(a,e) 求下面每个序列的 DTFT:
[!NOTE]
解:这种题要么代入定义式,要么用常用傅里叶变换对+性质。$y_1[n]$是常用变换对,但我依然写一下用定义求解的过程;$y_5[n]$经过分解后,可以利用 $y_1[n]$ 的结论求解。
$$ \begin{align} y_5[n] &= \begin{cases} \dfrac{e^{j\pi n/2N}+e^{-j\pi n/2N}}{2}, & -N\leq n \leq N\\ 0, & 其他 \end{cases}\\ Y_5(e^{j\omega})&=\frac{1}{2} \sum_{n=-N}^{N} \left( e^{j\pi n/2N}+e^{-j\pi n/2N} \right) \cdot e^{-j\omega n}\\ &=\frac{1}{2}\left\{ \frac{\sin[(-\pi /2N+\omega) (N+1/2)]}{\sin[(-\pi /2N+\omega)/2]}+\frac{\sin[(\pi /2N+\omega) (N+1/2)]}{\sin[(\pi /2N+\omega)/2]}\right\} \end{align} $$
[!TIP] 3.26 已知 $X(e^{j\omega})$ 是 $x[n]$ 的 DTFT,求 $Y(e^{j\omega})=\frac{1}{2}\{X(e^{j\omega/2})+X(-e^{j\omega/2})\}$ 的 IDTFT $y[n]$
[!NOTE] 解:这题主要考察的是性质。首先,由时域压缩性质可知 $X(e^{j\omega/2})\leftrightarrow x[2n]$,然后再由频移性质可知 $X(e^{j(\omega/2+\pi)})\leftrightarrow e^{j\pi n}x[2n]=(-1)^n x[2n]$,所以 :
$$ y[n]= \begin{cases} x[2n], &n为偶数\\ 0, &n为奇数 \end{cases} $$Tip
3.27 实序列 $x[n]$ 的 DTFT 为:
$$ X(e^{j\omega})=\frac{\alpha+\beta e^{j\omega}}{1+\gamma e^{j\omega}},|\gamma|< 1 $$求 $X(e^{j\omega})$ 的实部、虚部、幅度、相位,证明实部与幅度是 $\omega$ 的偶函数,虚部和相位是 $\omega$ 的奇函数。
[!NOTE] 解:题目并未说明 $\alpha,\beta,\gamma$ 的定义域,默认为实数域。
$$ \displaylines{ 实部:X_\text{re}(e^{j\omega})=\frac{1}{2} \left\{ X(e^{j\omega})+X^*(e^{j\omega}) \right\}=\frac{1}{2}\left( \frac{\alpha+\beta e^{j\omega}}{1+\gamma e^{j\omega}}+\frac{\alpha+\beta e^{-j\omega}}{1+\gamma e^{-j\omega}} \right)\\ 虚部:X_\text{im}(e^{j\omega})=\frac{1}{2} \left\{ X(e^{j\omega})-X^*(e^{j\omega}) \right\}=\frac{1}{2}\left( \frac{\alpha+\beta e^{j\omega}}{1+\gamma e^{j\omega}}-\frac{\alpha+\beta e^{-j\omega}}{1+\gamma e^{-j\omega}} \right)\\ 幅值:|X(e^{j\omega})|=\sqrt{\frac{(\alpha+\beta \cos\omega)^2+(\beta\sin\omega)^2}{(1+\gamma \cos\omega)^2+(\gamma\sin\omega)^2}}\\ 相位:\arg\{ X(e^{j\omega}) \}= \arctan \frac{\beta\sin\omega}{\alpha+\beta \cos\omega} - \arctan \frac{\gamma\sin\omega}{1+\gamma \cos\omega} } $$由于是实序列,所以无需求实部和虚部也知道,$X(e^{j\omega})$ 实部为偶函数、虚部为奇函数。至于幅度和相位,只需要代入 $-\omega$ 计算即可。
$$ \begin{align} \because\; &\cos(-\omega)=\cos\omega\\ &\sin (-\omega)=-\sin \omega\\ &\arctan (-\omega) = -\arctan \omega\\ \therefore\; &|X(e^{-j\omega})|=|X(e^{j\omega})|\\ &\arg\{ X(e^{-j\omega}) \}=-\arg\{ X(e^{j\omega}) \} \end{align} $$
Tip
3.60 对 4s 长的连续信号进行无混叠均匀抽样,抽取到 8500 个样本点,问连续信号中可能存在的最高频率成分是什么?
Note
解:根据采样定义,采样频率大于最高频的两倍,而采样频率 $f_s=8500/4=2.125 \text{kHz}$,故可能存在的最高频率成分为 $f_M\lt 2.125/2=1.0625 \text{kHz}$
Tip
3.65 最高频为 $\Omega_m$ 的信号(频谱图见课本)经过 $\omega_s=2\Omega_m$ 的理想采样,再经过截止频率为 $\omega_c=\Omega_m T_s/2$ 的低通滤波,再经过理想内插后,得到 $y_a(t)$,求 $Y_a(j\Omega)$
Note
解:按系统顺序分析就行了。先是抽样,频谱经过周期性延拓和压缩,$\pm\Omega_m$ 压缩到 $\pm\pi$ 的位置。
然后是低通滤波,截止频率 $\omega_c=\Omega_m T_s/2=\pi/2$,说明原来 $\Omega_m/2$ 以上的频率均被滤除。
然后再经过理想内插,得到 $Y_a(j\Omega)$ 的图像如下:
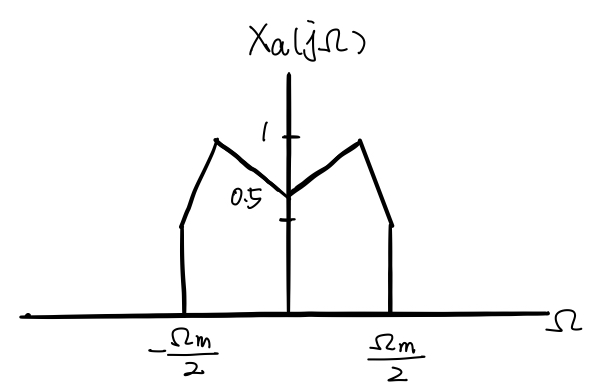
Caution
注:牢记数字频率、模拟频率、采样频率之间的关系式:$\omega_d = 2 \pi \dfrac{f_c}{f_s}$